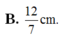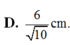Chọn C
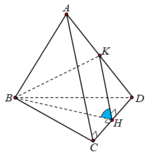
Gọi H là trung điểm cạnh CD và K là trung điểm cạnh AD.
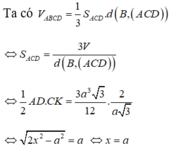
Tam giác ACD có CA=CD=x=a ; AD = a 2 => tam giác ACD vuông cân tại C
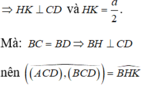
Mặt khác:
Tam giác ABD có:
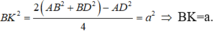
Tam giác BHK có:
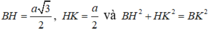
=> Tam giác BHK vuông tại H ⇒ B H K ^ = 90 o hay A C D , B C D ^ = 90 o
Chọn C

Gọi H là trung điểm cạnh CD và K là trung điểm cạnh AD.
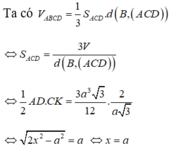
Tam giác ACD có CA=CD=x=a ; AD = a 2 => tam giác ACD vuông cân tại C
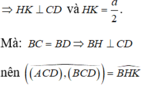
Mặt khác:
Tam giác ABD có:
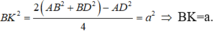
Tam giác BHK có:
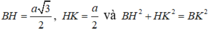
=> Tam giác BHK vuông tại H ⇒ B H K ^ = 90 o hay A C D , B C D ^ = 90 o
Cho tứ diện ABCD có B C = C D = B D = 2 a , A C = a 2 , A B = a . Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là
A. 90o.
B. 60o.
C. 45o.
D. 30o.
Cho tứ diện ABCD có CD=a 2 , ∆ ABC là tam giác đều cạnh a, ∆ ACD vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có AB=BC=AC=BD=2a, AD= a 3 ; hai mặt phẳng (ACD) và (BCD) vuông góc với nhau. Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có C D = a 2 , ∆ A B C là tam giác đều cạnh a, ∆ A C D vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích của khối cầu ngoại tiếp tứ diện ABCD bằng
A. 4 πa 3 3
B. πa 3 6
C. 4 πa 3
D. πa 3 3 2
Cho tứ diện ABCD có (ACD) ⊥ (BCD), AC = AD = BC = BD = a, CD = 2x . Giá trị của x để hai mặt phẳng (ABC) và (ABD) vuông góc với nhau là:
A. a 2 3
B. a 3 3
C. a 3 2
D. a 5 3
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D, AB = AD =a,CD = 2a. Hình chiếu của S lên mặt phẳng (ABCD) trùng với trung điểm của BD. Biết thể tích tứ diện SBCD bằng a 3 6 . Tính khoảng cách từ A đến mặt phẳng (SBC) là:
A. a 3 2
B. a 2 6
C. a 3 6
D. a 6 4
Cho tứ diện ABCD có B A C ^ = C A D ^ = D A B ^ = 90 0 , A B = a , A C = 2 , A D = 3 . Khoảng cách từ A đến mặt phẳng (BCD) là
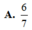
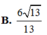
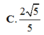
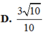
Tứ diện ABCD có AB, AC, AD đôi một vuông góc. Tam giác ABC cân tại A, có A B = 2 a , A C D = 60 o . M là trung điểm AB, N ∈ B C sao cho . Khi đó khoảng cách từ P đến mặt phẳng (BCD) bằng (với P là giao điểm MN và AC).
A. 2 a 21 7 .
B. a 21 7 .
C. a 7 7
D. 2 a 7 7
Cho tứ diện ABCD có cạnh DA vuông góc với mặt phẳng (ABC) và AB=3cm, AC=4cm, AD= 6 CM, BC=5cm. Khoảng cách từ A đến mặt phẳng (BCD) bằng