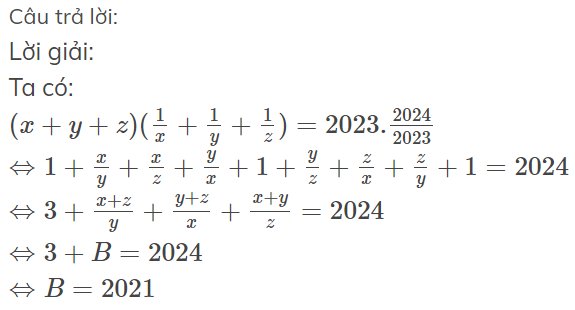x=-2023 

k nhé bạ 

x=-2023

câu này bằng 2023 nhé bạn

a: \(8x\left(2023+x\right)-8x\left(x+2024\right)=56\)

=>\(8x\left(x+2023-x-2024\right)=56\)

=>-8x=56

=>\(x=\frac{56}{-8}=-7\) (nhận)

b: \(5-2025x=9-2026\left(x-1\right)\)

=>-2025x+5=9-2026x+2026

=>-2025x+5=-2026x+2035

=>x=2035-5=2030(nhận)

c: \(\left(-12\right)^2\cdot x=56+10\cdot13x\)

=>144x=56+130x

=>14x=56

=>x=4(nhận)

d: -(x-32+11)=(21-33-x+7)

=>-(x-21)=(-x-5)

=>-x+21=-x-5

=>21=-5(vô lý)

=>x∈∅

e: \(-2\left(x+6\right)+6\left(x+10\right)=8\)

=>-2x-12+6x+60=8

=>4x+52=8

=>4x=8-52=-44

=>\(x=-\frac{44}{4}=-11\) (nhận)

Đề không đầy đủ. Bạn coi lại.

Với x = 2023 

<=> x + 1 = 2024

Khi đó P(2023) = x²⁰²³ - (x + 1).x²⁰²² + ... + (x + 1).x - 1

= x²⁰²³ - x²⁰²³ - x²⁰²² + .. + x² + x - 1

= x - 1 = 2023 - 1 = 2022

a: \(\left|a-2b+3\right|^{2023}>=0\forall a,b\)

\(\left(b-1\right)^{2024}>=0\forall b\)

Do đó: \(\left|a-2b+3\right|^{2023}+\left(b-1\right)^{2024}>=0\forall a,b\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}a-2b+3=0\\b-1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=1\\a=2b-3=2\cdot1-3=-1\end{matrix}\right.\)

Thay a=-1 và b=1 vào P, ta được:

\(P=\left(-1\right)^{2023}\cdot1^{2024}+2024=2024-1=2023\)

Đặt A=|x-2022|+|x-2023|+|x-2024|

TH1: x<2022

=>x-2022<0; x-2023<0; x-2024<0

=>A=-x+2022-x+2023-x+2024=-3x+6069

Vì hàm số A=-3x+6069 là hàm số nghịch biến trên R

nên A nhỏ nhất khi x lớn nhất

Khi x<2022 thì x không có giá trị lớn nhất

=>A không có giá trị nhỏ nhất(1)

TH2: 2022<=x<2023

=>x-2022>=0; x-2023<0; x-2024<0

=>A=x-2022+2023-x+2024-x=-x+2025

Vì hàm số A=-x+2025 là hàm số nghịch biến trên R

nên A nhỏ nhất khi x lớn nhất

Khi 2022<=x<2023 thì x không có giá trị lớn nhất

=>A không có giá trị nhỏ nhất(2)

TH3: 2023<=x<2024

=>x-2022>0; x-2023>=0; x-2024<0

=>A=x-2022+x-2023+2024-x=x-2021

Vì hàm số A=x-2021 là hàm số đồng biến trên R

nên A nhỏ nhất khi x nhỏ nhất

Khi 2023<=x<2024 thì \(x_{\min}=2023\)

=>A min=2023-2021=2(3)

TH4: x>=2024

=>x-2022>0; x-2023>0; x-2024>=0

=>A=x-2022+x-2023+x-2024=3x-6069

Vì hàm số A=3x-6069 là hàm số đồng biến trên R

nên A nhỏ nhất khi x nhỏ nhất

Khi x>=2024 thì \(x_{\min}=2024\)

=>\(A_{\min}=3\cdot2024-6069=6072-6069=3\) (4)

Từ (1),(2),(3),(4) suy ra \(A_{\min}=3\) khi x=2023

Ta có: \(P=\frac{|x-2022|+|x-2023|+|x-2024|+2022}{|x-2022|+|x-2023|+|x-2024|}\)

\(=1+\frac{2022}{|x-2022|+|x-2023|+|x-2024|}=1+\frac{2022}{A}\)

\(A\ge3\forall x\)

=>\(\frac{2022}{A}\le\frac{2022}{3}=674\forall x\)

=>\(1+\frac{2022}{A}\le1+674=675\forall x\)

=>P<=675∀x

Dấu '=' xảy ra khi x=2023

Lời giải:
Ta có:
$(x+y+z)(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})=2023.\frac{2024}{2023}$

$\Leftrightarrow 1+\frac{x}{y}+\frac{x}{z}+\frac{y}{x}+1+\frac{y}{z}+\frac{z}{x}+\frac{z}{y}+1=2024$

$\Leftrightarrow 3+\frac{x+z}{y}+\frac{y+z}{x}+\frac{x+y}{z}=2024$

$\Leftrightarrow 3+B=2024$

$\Leftrightarrow B=2021$