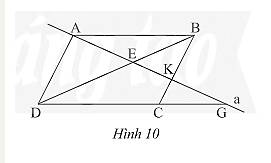
a) Vì \(ABCD\) là hình bình hành nên \(AB//CD;AD//BC\)

\( \Rightarrow AB//DG;AB//CG;BK//AD;KC//AD\)

Xét tam giác \(DEG\) có \(AB//DG\), theo hệ quả của định lí Thales ta có:

\(\frac{{AE}}{{EG}} = \frac{{EB}}{{ED}}\) (1)

Xét tam giác \(ADE\) có \(BK//AD\), theo hệ quả của định lí Thales ta có:

\(\frac{{EK}}{{AE}} = \frac{{EB}}{{ED}}\) (2)

Từ (1) và (2) suy ra, \(\frac{{AE}}{{EG}} = \frac{{EK}}{{AE}} \Rightarrow A{E^2} = EG.EK\) (điều phải chứng minh).

b) Xét tam giác \(AED\) có:

\(AD//BK \Rightarrow \frac{{AE}}{{AK}} = \frac{{DE}}{{DB}}\)(3)

Xét tam giác \(AEB\) có

\(AB//BK \Rightarrow \frac{{AE}}{{AG}} = \frac{{BE}}{{BD}}\) (4)

Từ (3) và (4) ta được:

\(\frac{{AE}}{{AK}} + \frac{{AE}}{{AG}} = \frac{{DE}}{{BD}} + \frac{{BE}}{{BD}} = \frac{{BD}}{{BD}} = 1\)

Ta có: \(\frac{{AE}}{{AK}} + \frac{{AE}}{{AG}} = 1 \Rightarrow \frac{1}{{AE}} = \frac{1}{{AK}} + \frac{1}{{AG}}\) (chia cả hai vế cho \(AE\)) (điều phải chứng minh).

Ai tk mình đi mình bị âm nè!

Ai tk mình mình tk lại!!!

ahihi

trả lời giúp đi ạ 

Do AB song song Cd 

=> Áp dụng định lí Ta - lét được \(\frac{AB}{DG}=\frac{AE}{EG}=\frac{BE}{DE}\)

=> AB . EG = DG . AE

Do AD song song BK nên áp dụng định lí Ta lét được

\(\frac{AE}{AK}=\frac{DE}{BD}\)

Do AB sog song với CG nên áp dụng định lí Ta lét được

\(\frac{AE}{AG}=\frac{BE}{BD}\)

=> \(\frac{AE}{AK}+\frac{AE}{AG}=\frac{BE}{BD}+\frac{DE}{BD}=1\)

=>\(\frac{1}{AE}=\frac{1}{AK}+\frac{1}{AG}\)

Ta có \(\frac{BK}{AD}=\frac{AB}{DG}=\frac{BE}{DE}\)

=>\(BK.DG=AB.AD\left(KHÔNG\right)DOI\)

bó tay .com

bo tay luon

b)

AB // DG suy ra AE / AG = BE / BD

AD // BC suy ra AE / AK = DE / BD

Suy ra AE / AG + AE / AK = BE /BD + DE / BD = BD / BD = 1

Chia 2 vế cho AE

1 / AG + 1 / AK = 1/  AE

a) AB // CG suy ra AE / EG = BE / ED

AD // BC suy ra EK / AE = BE / ED

Suy ra AE / EG = EK / AE

Suy ra AE^2 = EK.EG

a) Vì ABCD là hình bình hành ( gt )

Và K thuộc BC nên

AD // BK Theo hệ quả của định lý Ta-let ta có :

\(\frac{EK}{AE}=\frac{EB}{ED}=\frac{AE}{EG}\Rightarrow\frac{EK}{AE}=\frac{AF}{EG}\Rightarrow AE^2=EK.EG\)

b) Ta có :

\(\frac{AE}{EK}-\frac{DE}{DB};\frac{AE}{AG}=\frac{BE}{BD}\)nên

\(\frac{AE}{AK}+\frac{AE}{AG}-\frac{BE}{BD}+\frac{DE}{DB}-\frac{BD}{BD}-1\Rightarrow\frac{1}{AE}=\frac{1}{AK}+\frac{1}{AG}\)

c) bạn tự làm tiếp mỏi tay quá

Giải nốt bài của Pác Hiếu:3

Đặt \(AB=a',AD=b\)

Áp dụng Đ/L Thales vào tam giác ABK,ta có:

\(\frac{BK}{KC}=\frac{AB}{CG}\Rightarrow\frac{a'}{CG}=\frac{BK}{KC}\left(1\right)\)

Áp dụng Đ/L Thales vào tam giác ADG,ta có:

\(\frac{CG}{DG}=\frac{CK}{AD}\Rightarrow\frac{CG}{DG}=\frac{CK}{b}\left(2\right)\)

Nhân vế theo vế của (1);(2) ta có:

\(\frac{BK}{b}=\frac{a'}{DG}\Rightarrow BK\cdot DG=a'b\)  không đổi.

Bài giải:

Chiều rộng hình chữ nhật là:

        12 : 4 = 3 ( dm)

Chu vi mảnh tấm bìa đó  là:

        ( 12 + 3 ) x 2 = 30 ( dm)

                 Đáp số: 30dm.