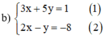
Từ (2) ta rút ra được y = 2x + 8 (*)

Thế (*) vào phương trình (1) ta được :

3x + 5(2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.

Thay x = - 3 vào (*) ta được y = 2.(-3) + 8 = 2.

Vậy hệ phương trình có nghiệm duy nhất (-3 ; 2).

Phép chia hết xảy ra khi \(\left\{{}\begin{matrix}n+1\le3\\n+3\le5\end{matrix}\right.\Leftrightarrow n\le2\)

Cách 1

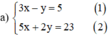
Từ (1) ta rút ra được y = 3x – 5 (*)

Thế (*) vào phương trình (2) ta được :

5x + 2(3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.

Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.

Vậy hệ phương trình có nghiệm duy nhất (3 ; 4).

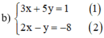
Từ (2) ta rút ra được y = 2x + 8 (*)

Thế (*) vào phương trình (1) ta được :

3x + 5(2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.

Thay x = - 3 vào (*) ta được y = 2.(-3) + 8 = 2.

Vậy hệ phương trình có nghiệm duy nhất (-3 ; 2).

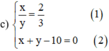
Từ (1) ta rút ra được x = 2 3 y  (*)

Thế (*) vào phương trình (2) ta được :

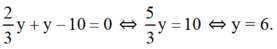
Thay y = 6 vào (*) ta được x = 4.

Vậy hệ phương trình có nghiệm duy nhất (x ; y) = (4 ; 6).

Cách 2

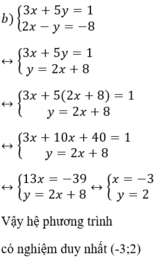
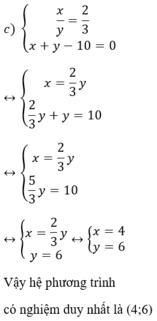
Kiến thức áp dụng

+ Giải hệ phương trình 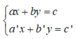 ta làm như sau:

Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).

Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .

Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.

+ Nếu xuất hiện phương trình dạng 0x = a (hoặc 0y = a) thì ta kết luận hệ phương trình vô nghiệm nếu a ≠ 0 hoặc hệ có vô số nghiệm nếu a = 0.

http://lovelove.xtreemhost.com/nguhaykhong.html?i=1

\(pkkikkkkkk\min\limits_{kkkkk\max\limits_{ }kkkk\lim\limits_{\rightarrow}kkkk\sqrt{ }kkk\sqrt{ }\sqrt{ }\sqrt{ }\sqrt{ }\sqrt{ }\sqrt{ }\sqrt{ }\sqrt{ }\sqrt{ }k\sqrt{ }k\sqrt{ }\sqrt{ }\sqrt{ }k\sqrt{ }\sqrt{ }k\sqrt{ }k\sqrt{ }k\sqrt{ }\sqrt{ }\sqrt{ }\sqrt{ }k\sqrt{ }\sqrt{ }\sqrt{ }\sqrt{ }}\)

12x-21=5y

do 12,21 chia hết cho 3 => 5y chia hết cho 3 => y=3k

\(\dfrac{1}{2}\left(6x-2y\right)\left(3x+y\right)=\dfrac{1}{2}.2\left(3x-y\right)\left(3x+y\right)=9x^2-y^2\)

\(\left(\dfrac{2}{3}z-\dfrac{2}{5}x\right)\left(\dfrac{1}{3}z+\dfrac{1}{5}x\right).\dfrac{1}{2}=\left(\dfrac{1}{3}z-\dfrac{1}{5}x\right)\left(\dfrac{1}{3}z+\dfrac{1}{5}z\right).2.\dfrac{1}{2}=\dfrac{1}{9}z^2-\dfrac{1}{25}x^2\)

\(\left(5y-3x\right).\dfrac{1}{4}\left(12x+20y\right)=\left(5y-3x\right)\left(5y+3x\right).4.\dfrac{1}{4}=25y^2-9x^2\)

\(\left(\dfrac{3}{4}y-\dfrac{1}{2}x\right)\left(x+\dfrac{3}{2}y\right)=\left(\dfrac{3}{2}y-x\right)\left(\dfrac{3}{2}y+x\right)=\dfrac{9}{4}y^2-x^2\)

\(\left(a+b+c\right)\left(a+b+c\right)=\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ac\)

\(\left(x-y+z\right)\left(x+y-z\right)=x^2-\left(y-z\right)^2=x^2-y^2-z^2+2yz\)

a: \(\dfrac{1}{2}\left(6x-2y\right)\left(3x+y\right)=\left(3x-y\right)\cdot\left(3x+y\right)=9x^2-y^2\)

b: \(\left(\dfrac{2}{3}z-\dfrac{2}{5}x\right)\left(\dfrac{1}{3}z+\dfrac{1}{5}x\right)\cdot\dfrac{1}{2}\)

\(=\left(\dfrac{1}{3}z-\dfrac{1}{5}x\right)\left(\dfrac{1}{3}z+\dfrac{1}{5}x\right)\)

\(=\dfrac{1}{9}z^2-\dfrac{1}{25}x^2\)

c: \(\left(5y-3x\right)\cdot\dfrac{1}{4}\cdot\left(12x+20y\right)\)

\(=\left(5y-3x\right)\left(5y+3x\right)\)

\(=25y^2-9x^2\)

d: \(\left(\dfrac{3}{4}y-\dfrac{1}{2}x\right)\left(\dfrac{3}{2}y+x\right)\cdot2\)

\(=\left(\dfrac{3}{2}y-x\right)\left(\dfrac{3}{2}y+x\right)\)

\(=\dfrac{9}{4}y^2-x^2\)

e: \(\left(a+b+c\right)\left(a+b-c\right)\)

\(=\left(a+b\right)^2-c^2\)

\(=a^2+2ab+b^2-c^2\)

Ta có : \(\frac{12x^2+12x+11}{4x^2+4x+3}=\frac{5y^2-10y+9}{y^2-2y+2}\)

\(\Leftrightarrow\frac{3\left(4x^2+4x+3\right)+2}{4x^2+4x+3}=\frac{5\left(y^2-2y+2\right)-1}{y^2-2y+2}\)

\(\Leftrightarrow3+\frac{2}{4x^2+4x+3}=5-\frac{1}{y^2-2y+2}\)

Do \(\frac{2}{4x^2+4x+3}=\frac{2}{\left(2x+1\right)^2+2}\le\frac{2}{2}=1\) \(\Rightarrow3+\frac{2}{4x^2+4x+3}\le4\left(1\right)\)

\(\frac{1}{y^2-2y+2}=\frac{1}{\left(y-1\right)^2+1}\le\frac{1}{1}=1\) \(\Rightarrow5-\frac{1}{y^2-2y+2}\ge5-1=4\left(2\right)\)

Từ ( 1 ) ; ( 2 ) \(\Rightarrow VT=VP=4\)

Dấu " = " xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}2x+1=0\\y-1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-\frac{1}{2}\\y=1\end{matrix}\right.\)

Vậy ....