Từ 1 điểm m ở ngoài (O) kẻ tiếp tuyến n là tiếp điểm. Gọi K là trung điểm MN, kẻ tiếp tuyến KI với đường tròn O (I là tiếp điểm).
a) CM R\(\Delta\)MNI là tam giác vuông.
b) Vẽ đường kính NJ của (O). CM 3 điểm M,I,J thẳng hàng.

Những câu hỏi liên quan
Từ 1 điểm m ở ngoài (O) kẻ tiếp tuyến n là tiếp điểm. Gọi K là trung điểm MN, kẻ tiếp tuyến KI với đường tròn O (I là tiếp điểm).
a) CM RDeltaMNI là tam giác vuông.
b) Vẽ đường kính NJ của (O). CM 3 điểm M,I,J thẳng hàng.
Đọc tiếp
Từ 1 điểm m ở ngoài (O) kẻ tiếp tuyến n là tiếp điểm. Gọi K là trung điểm MN, kẻ tiếp tuyến KI với đường tròn O (I là tiếp điểm).
a) CM R\(\Delta\)MNI là tam giác vuông.
b) Vẽ đường kính NJ của (O). CM 3 điểm M,I,J thẳng hàng.
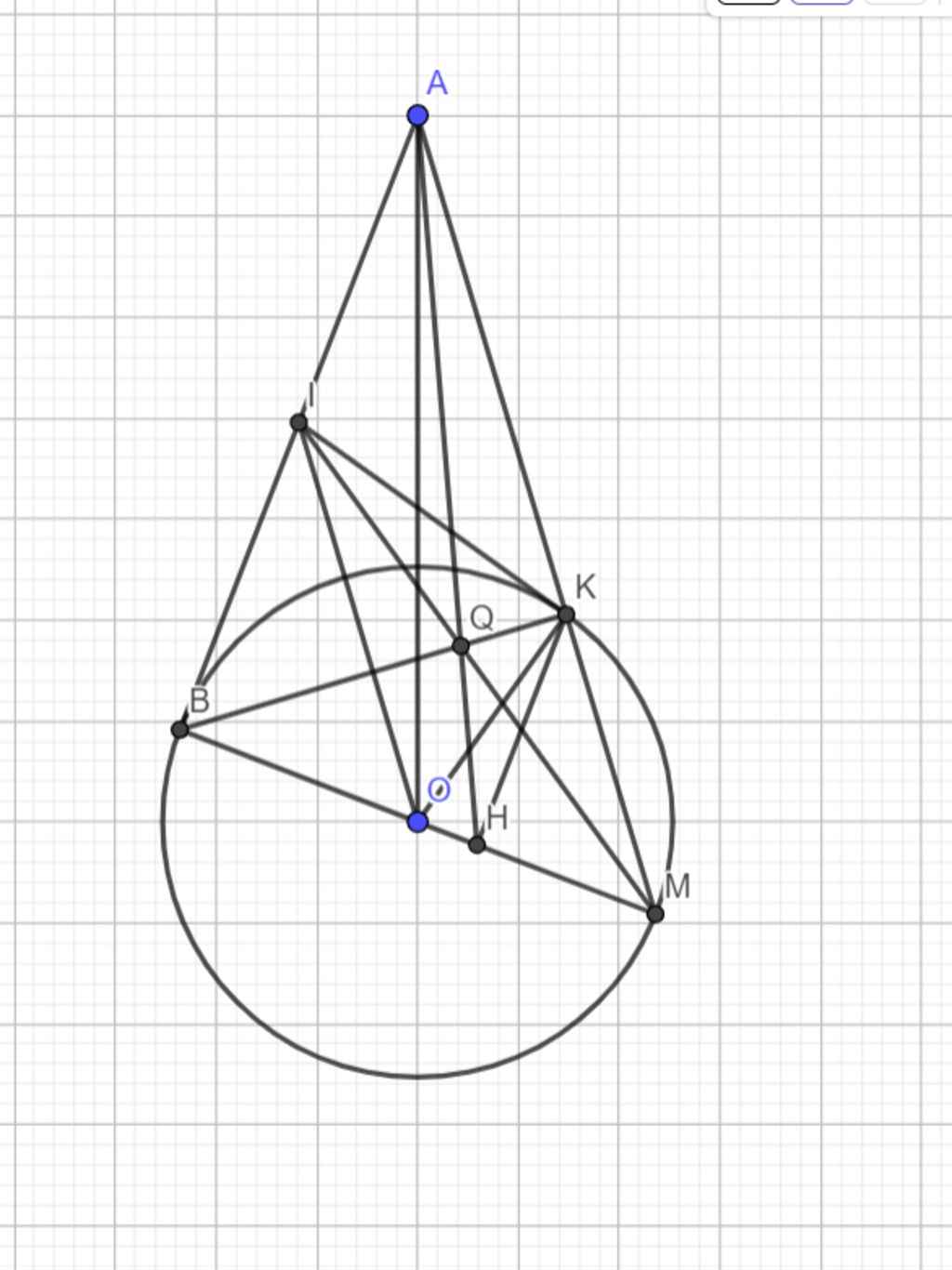
Từ một điểm ở ngoài đường tròn (O) kẻ tiếp tuyến AB với đường tròn (O) , (B là tiếp điểm ) . Gọi I là trung điểm của đoạn AB , kẻ tiếp tuyến IM với đường tròn (O) , (M là tiếp điểm )
a, CMR : Tam gTam ABM là tam giác vuông
b, vẽ đường kính BC của đường tròn (O). CM : 3 điểm A,M,C thẳng hàng
c , biết AB =8 cm, AC=10cm .tính độ dài đoạn thẳng AM
Từ một điểm A ở ngoài đường tròn (O;R), kẻ tiếp tuyến AB với đường trong (B là tiếp điểm). Gọi I là trung điểm của đoạn thẳng AB, kẻ tiếp tuyến IM (M là tiếp điểm) với đường tròn (O).
a) Chứng minh rằng : tam giác AIM cân.
b) Gọi K là giao điểm của OI và BM. Chứng minh rằng: AM =2.IK.
c) Tính OI, biết R=4cm, BM=6cm.
help tui với
a: Xét (O) có
IB,IM là tiếp tuyến
nên IB=IM=IA
=>ΔIMA cân tại I
b: IB=IM
OB=OM
Do đó: OI là trung trực của BM
=>OI vuông góc với BM
=>K là trung điểm của BM
Xét ΔBMA có BK/BM=BI/BA
nên KI//MA và KI=1/2MA
=>AM=2KI
c: BK=BM/2=3cm
\(OK=\sqrt{4^2-3^2}=\sqrt{7}\left(cm\right)\)
\(OK\cdot OI=OB^2\)
=>OI*căn 7=6^2=36
=>\(OI=\dfrac{36}{\sqrt{7}}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho đường tròn (O;R). Từ điểm A nằm ngoài đường tròn vẽ tiếp tuyến AB với(O) ( với B là tiếp tuyến ). Kẻ đường kính BM của đường tròn tâm O, AM cắt (O) tại K ( K ≠ M )a, Chứng minh tam giác BMK vuông, từ đó chứng minh AB2 AM.AKb, Gọi I là trung điểm của AB Chứng minh IK là tiếp tuyến của (O).
Đọc tiếp
Cho đường tròn (O;R). Từ điểm A nằm ngoài đường tròn vẽ tiếp tuyến AB với(O) ( với B là tiếp tuyến ). Kẻ đường kính BM của đường tròn tâm O, AM cắt (O) tại K ( K ≠ M )
a, Chứng minh tam giác BMK vuông, từ đó chứng minh AB2 =AM.AK
b, Gọi I là trung điểm của AB> Chứng minh IK là tiếp tuyến của (O).
a) Ta có \(I\) là trung điểm \(AB,O\) là trung điểm \(BM\)
\(\rightarrow IO\) là đường trung bình \(\Delta ABM\rightarrow OI\text{/ / }AM\rightarrow OI\text{/ / }KM\)
Vì \(BM\) là đường kính của \(O\)\(\rightarrow BK\text{⊥}KM\rightarrow OI\text{⊥}BK\)
\(\rightarrow B,K\) đối xứng qua \(OI\)
\(\rightarrow\widehat{IKO=\widehat{IBO}=90^o}\)
\(\rightarrow IK\) là tiếp tuyền của \(O\)
Biết mỗi làm câu A
Đúng 0
Bình luận (0)
a, ^BKM = 900 ( góc nt chắn nửa đường tròn )
Xét tam giác BMK có : ^BKM = 900
Vậy tam giác BMK vuông tại K
Vì AB là tiếp tuyến đường tròn (O) => ^ABO = 900
Xét tam giác ABM vuông tại B có BK là đường cao
\(AB^2=AK.AM\)( hệ thức lượng )
b, Ta có : ^BKM = 900 ( góc nt chắn nửa đường tròn )
=> ^BKA = 900
Xét tam giác BKA vuông tại K, có I là trung điểm AB
=> IK = IA = IB
Xét tam giác IKO và tam giác IBO có :
IK = IB ( cmt )
IO _ chung
OK = OB = R
Vậy tam giác IKO = tam giác IBO ( c.c.c )
=> ^IKO = ^IBO = 900 ( 2 góc tương ứng )
Xét (O) có : K thuộc IK; K thuộc (O)
=> IK là tiếp tuyến đường tròn (O)
Đúng 1
Bình luận (4)
(2 điểm) Từ 1 điểm A ở ngoài đường tròn (O), kẻ tiếp tuyến AB với đường tròn (O)
( B là tiếp điểm). Gọi I là trung điểm của đoạn thẳng AB, kẻ tiếp tuyến IM với đường tròn (O) ( M là tiếp điểm).
a)Chứng minh IA = IM.
b)Chứng minh Tam giác ABM là tam giác vuông tại M.
c)Vẽ đường kính BC của đường tròn (O). Chứng minh 3 điểm A, M, C thẳng hàng.
a: Xét (O) có
IM là tiếp tuyến
IB là tiếp tuyến
Do đó: IM=IB
mà IA=BI
nên IA=IM
b: Xét ΔABM có
MI là đường trung tuyến
MI=AB/2
Do đó: ΔMAB vuông tại M
c: Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó: ΔBMC vuông tại M
hay BM⊥CM
mà BM⊥AM
và CM,AM có điểm chung là M
nên A,M,C thẳng hàng
Đúng 1
Bình luận (0)
Từ điểm A ở ngoài đường tròn [O;R] vẽ hai tiếp tuyến AB;AC với đường tròn [B,C là tiếp điểm ]. Gọi H là chân đường vuông góc kẻ từ B đến đường kính CD.
a cm 4 điểm A,B,C,O cùng thuộc 1 đường tròn
b cm BD //OA
c i là giao điểm BH và AD. Cm i là trung điểm bh
Giúp em phần c với ạ!
c: IH vuông góc CD
AC vuông góc CD
DO đó: IH//AC
Xét ΔDCA có IH//AC
nên \(\dfrac{IH}{AC}=\dfrac{DH}{DC}\)
=>\(IH=\dfrac{AC\cdot DH}{DC}\)
Xét ΔACO vuông tại C và ΔBHD vuông tại H có
\(\widehat{AOC}=\widehat{BDH}\left(=\widehat{AOB}\right)\)
Do đó: ΔACO đồng dạng với ΔBHD
=>\(\dfrac{AC}{BH}=\dfrac{CO}{HD}\)
=>\(BH=\dfrac{AC\cdot HD}{CO}\)
\(\dfrac{BH}{IH}=\dfrac{DO}{OC}=2\)
=>BH=2IH
=>I là trung điểm của BH
Đúng 0
Bình luận (0)
Giải giúp mình các bài này với ạ!1) Từ điểm A nằm ngoài đường tròn tâm O, vẽ tiếp tuyến AB (B là tiếp điểm). Lấy điểm C thuộc đường tròn tâm (O) khác điểm B sao cho AB ACa. CM : Tam giác OAB tam giác OACb. CM : AC là tiếp tuyến của đường tròn tâm Oc. Gọi I là giao điểm của OA và BC. Tính AB biết bán kính (R) 5cm, BC 8cm2) Lấy 2 điểm A và B thuộc đường tròn tâm O (3 điểm A, B, O không thẳng hàng). Tiếp tuyến của O tại A cắt tia phân giác của góc AOB tại C.a. So sánh tam giác OAC và tam giác O...
Đọc tiếp
Giải giúp mình các bài này với ạ!
1) Từ điểm A nằm ngoài đường tròn tâm O, vẽ tiếp tuyến AB (B là tiếp điểm). Lấy điểm C thuộc đường tròn tâm (O) khác điểm B sao cho AB = AC
a. CM : Tam giác OAB = tam giác OAC
b. CM : AC là tiếp tuyến của đường tròn tâm O
c. Gọi I là giao điểm của OA và BC. Tính AB biết bán kính (R) = 5cm, BC = 8cm
2) Lấy 2 điểm A và B thuộc đường tròn tâm O (3 điểm A, B, O không thẳng hàng). Tiếp tuyến của O tại A cắt tia phân giác của góc AOB tại C.
a. So sánh tam giác OAC và tam giác OBC.
b. CM : BC là tiếp tuyến của đường tròn tâm O
3) Cho đường tròn tâm O, bán kính R. Lấy điểm A cách O một khoảng = 2R. Từ A vẽ 2 tiếp tuyến AB, AC (B,C là tiếp điểm). OA cắt đường tròn tâm O tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.
a. CM : OK // AB
b. CM : tam giác OAK là tam giác cân
c. CM : KI là tiếp tuyến của đường tròn tâm O.
Cho điểm A cố định ở bên ngoài đường trong tâm O, kẻ các tiếp tuyến AM, AN vs đường tròn (M, N là các tiếp điểm). Vẽ cát tuyến ABC vs đường tròn (O) (B nằm giữa A và C). Gọi I là trung điểm của BC. a. CM tứ giác AMON nội tiếp đường tròn b.Gọi k là giao điểm của MN và BC. CM AK.AI=AB.AC
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: ΔOBC cân tại O có OI là trung tuyến
nên OI vuông góc BC
Xét (O) có
AM,AN là tiếp tuyến
=>AM=AN
mà OM=ON
nên OA là trung trực của MN
=>OA vuông góc MN tại H
Xét ΔAHK vuông tại H và ΔAIO vuông tại I có
góc HAK chung
=>ΔAHK đồng dạng vớiΔAIO
=>AH/AI=AK/AO
=>AH*AO=AK*AI=AB*AC
Đúng 0
Bình luận (0)
Cho (O;R). Từ 1 điểm A ở ngoài đường tròn tâm O, vẽ các tiếp tuyến AB, AC với (O) có B, C là tiếp điểm. Gọi H là giao điểm của AO và dây BC. Kẻ đường kính BD. a, CM 4 điểm A, B, O, C cùng thuộc 1 đường tròn. b, Tiếp tuyến của (O) tại D cắt BC tại E. CM tam giác ACD đồng dạng vs tam giác OCE. Giúp mk phần b nhaa *-*
a: Xét tứ giácc ABOC có
góc OBA+góc OCA=180 độ
nen ABOC là tứ giác nội tiếp
b: Xét ΔCAO vuông tại C và ΔCDE vuông tại C có
góc CAO=góc CDE
Do đó: ΔCAO đồng dạng vơi ΔCDE
=>CA/CD=CO/CE
=>CA/CO=CD/CE
Xét ΔCAD và ΔCOE có
CA/CO=CD/CE
góc ACD=góc OCE
Do đo: ΔCAD đồng dạng với ΔCOE
Đúng 0
Bình luận (0)