1 tổ chuyên môn gồm 7 thầy và 5 cô. Chọn ngẫu nhiên 5 người để lập hội đồng thi. Tính xác suất: A: 5 người được chọn có ít nhất 3 cô. B: 5 người được chọn có đúng 3 thầy. C: 5 người được chọn có cả thầy và cô.

Những câu hỏi liên quan
Một tổ chuyên môn gồm 7 thầy và 5 cô giáo, trong đó thầy An và cô Bình là vợ chồng. Chọn ngẫu nhiên 5 người để lập hội đồng chấm thi vấn đáp. Có bao nhiêu cách lập sao cho hội đồng có 3 thầy, 2 cô và nhất thiết phải có thầy An hoặc cô Bình nhưng không có cả hai. A: 140 B: 250 C: 200 D: 120
Đọc tiếp
Một tổ chuyên môn gồm 7 thầy và 5 cô giáo, trong đó thầy An và cô Bình là vợ chồng. Chọn ngẫu nhiên 5 người để lập hội đồng chấm thi vấn đáp. Có bao nhiêu cách lập sao cho hội đồng có 3 thầy, 2 cô và nhất thiết phải có thầy An hoặc cô Bình nhưng không có cả hai.
A: 140
B: 250
C: 200
D: 120
TH1. hội đồng gồm 3 thầy, 2 cô trong đó có thầy An nhưng không có cô Bình.
Khi đó ta cần chọn 2 trong 6 thầy còn lại (trừ thầy An) rồi chọn 2 trong 4 cô (trừ cô Bình)
Có C 6 2 . C 4 2 = 60
TH2. hội đồng gồm 3 thầy, 2 cô trong đó có cô Bình nhưng không có thầy An.
Khi đó ta cần chọn 3 trong 6 thầy còn lại (trừ thầy An) rồi chọn 1 trong 4 cô (trừ cô Bình)
Có C 6 3 . C 4 1 = 80
Vậy, có 60+80=140 cách lập hội đồng coi thi.
Chọn A.
Đúng 0
Bình luận (0)
1 tổ có 8 nữ, 9 nam chọn ngẫu nhiên 1 nhóm 5 người . tính xác suất để
a trong 5 người chọn được có đúng 3 nam
b trong 5 người chọn đc có nhiều nhất 1 nữ
Không gian mẫu: \(C_{17}^5\)
a. Số cách chọn sao cho có đúng 3 nam (nghĩa là chọn 3 nam từ 9 nam và 2 nữ từ 8 nữ):
\(n_A=C_9^3.C_8^2\)
Xác suất: \(P_A=\dfrac{C_9^3.C_8^2}{C_{17}^5}=...\)
b. Chọn nhiều nhất 1 nữ nghĩa là ta có 2 TH có thể xảy ra: có 1 nữ và 4 nam hoặc cả 5 đều nam
Số cách chọn: \(n_B=C_8^1.C_4^9+C_9^5\)
Xác suất: \(P_B=\dfrac{C_8^1.C_9^4+C_9^5}{C_{17}^5}=...\)
Đúng 2
Bình luận (0)
Một đội ngũ giáo viên gồm 8 thầy giáo dạy toán, 5 cô giáo dạy vật lý và 3 cô giáo dạy hóa học. Sở giáo dục cần chọn ra 4 người để chấm bài thi THPT quốc gia, tính xác suất trong 4 người được chọn phải có cô giáo và có đủ ba bộ môn A.
5
9
B.
3
7
C.
4
7
D.
4
9
Đọc tiếp
Một đội ngũ giáo viên gồm 8 thầy giáo dạy toán, 5 cô giáo dạy vật lý và 3 cô giáo dạy hóa học. Sở giáo dục cần chọn ra 4 người để chấm bài thi THPT quốc gia, tính xác suất trong 4 người được chọn phải có cô giáo và có đủ ba bộ môn
A. 5 9
B. 3 7
C. 4 7
D. 4 9
Một đội ngũ giáo viên gồm 8 thầy giáo dạy toán, 5 cô giáo dạy vật lý và 3 cô giáo dạy hóa học. Sở giáo dục cần chọn ra 4 người để chấm bài thi THPT quốc gia, tính xác suất trong 4 người được chọn phải có cô giáo và có đủ ba bộ môn A. B. C. D.
Đọc tiếp
Một đội ngũ giáo viên gồm 8 thầy giáo dạy toán, 5 cô giáo dạy vật lý và 3 cô giáo dạy hóa học. Sở giáo dục cần chọn ra 4 người để chấm bài thi THPT quốc gia, tính xác suất trong 4 người được chọn phải có cô giáo và có đủ ba bộ môn
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án B
Ta có: chọn ra 4 thầy cô từ 16 thầy cô có ![]() (cách chọn)
(cách chọn)
+ Để chọn được 4 giáo viên phải có cô giáo và đủ ba bộ môn, vậy có các trường hợp sau:
* Trường hợp 1: chọn 2 thầy toán, 1 cô lý, 1 cô hóa có ![]() (cách chọn)
(cách chọn)
* Trường hợp 2: chọn 1 thầy toán, 2 cô lý, 1 cô hóa có ![]() (cách chọn)
(cách chọn)
* Trường hợp 3: chọn 1 thầy toán, 1 cô lý, 2 cô hóa có ![]() (cách chọn)
(cách chọn)
Vậy xác suất để chọn được 4 người phải có cô giáo và có đủ ba bộ môn là
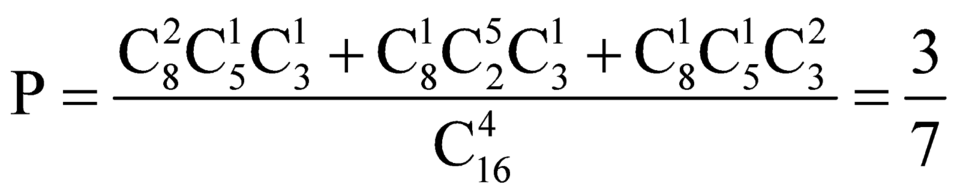
Đúng 0
Bình luận (0)
Tổ toán của một trường THPT có 4 thầy giáo và 10 cô giáo. Tổ chọn ngẫu nhiên 2 giáo viên để đi tập huấn. Tính xác suất để 2 giáo viên được chọn gồm 1 thầy giáo và 1 cô giáo.
A
.
45
91
B
.
10
91
C
.
40
91
D
.
20
91
Đọc tiếp
Tổ toán của một trường THPT có 4 thầy giáo và 10 cô giáo. Tổ chọn ngẫu nhiên 2 giáo viên để đi tập huấn. Tính xác suất để 2 giáo viên được chọn gồm 1 thầy giáo và 1 cô giáo.
A . 45 91
B . 10 91
C . 40 91
D . 20 91
Chọn C
Gọi biến cố A: “2 giáo viên tập huấn gồm 1 thầy giáo và 1 cô giáo”.
Suy ra ![]() .
.
Vậy 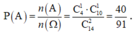 .
.
Đúng 0
Bình luận (0)
Một tổ gồm 7 nam và 3 nữ. Chọn ngẫu nhiên hai người. Xác suất để trong hai người được chọn có ít nhất một nữ là:
A. \(\frac{7}{{15}}\)
B. \(\frac{8}{{15}}\)
C. \(\frac{1}{{15}}\)
D. \(\frac{2}{{15}}\)
Số cách chọn 2 bạn bất kì trong 10 bạn đó là \(C_{10}^2\)
Cách 1:
Trường hợp 1: Hai bạn được chọn gồm 1 nam và 1 nữ
Có 7 cách chọn một bạn nam
Có 3 cách chọn một bạn nữ
=> Có 3.7 =21 cách chọn
Trường hợp 2: Hai bạn được chọn đều là nữ
Số cách chọn 2 trong 3 bạn nữ là: \(C_3^2\)
=> Xác suất để trong hai người được chọn có ít nhất một nữ là: \(\frac{{21 + C_3^2}}{{C_{10}^2}} = \frac{8}{{15}}\)
Chọn B.
Cách 2:
Gọi A là biến cố: “trong hai người được chọn có ít nhất một nữ”
Biến cố đối \(\overline A \): “trong hai người được không có bạn nữ nào” hay “hai người được chọn đều là nam”
Ta có: Số cách chọn 2 trong 7 bạn nam là \(n(\overline A ) = C_7^2\)
\(\begin{array}{l} \Rightarrow P(\overline A ) = \frac{{C_7^2}}{{C_{10}^2}} = \frac{{21}}{{45}} = \frac{7}{{15}}\\ \Rightarrow P(A) = 1 - P(\overline A ) = 1 - \frac{7}{{15}} = \frac{8}{{15}}\end{array}\)
Chọn B.
Đúng 0
Bình luận (0)
Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho hai người được chọn có ít nhất một nữ.
Đọc tiếp
Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho hai người được chọn có ít nhất một nữ.
![]()
![]()
![]()
![]()
Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho hai người được chọn có ít nhất một nữ. A.
7
15
B.
8
15
C.
1
5
D.
1
15
Đọc tiếp
Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho hai người được chọn có ít nhất một nữ.
A. 7 15
B. 8 15
C. 1 5
D. 1 15
Chọn B.
Phương pháp
Tính xác suất theo định nghĩa P A = n A n Ω với n(A) là số phần tử của biến cố A, n Ω là số phấn tử
của không gian mẫu.
Cách giải:
Số phần tử của không gian mẫu n Ω = C 20 2
Gọi A là biến cố “Hai người được chọn có it nhất một nữ” thì A là biến cố hai người được chọn không có nữ nào, tức là ta chọn 2 người trong số 7 nam.
Khi đó n A = C 7 2 ⇒ n A = C 10 2 - C 7 2
Xác suất để hai người được chọn có it nhất một nữ là P = C 10 2 - C 7 2 C 10 2 = 8 15
Đúng 0
Bình luận (0)
Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn có ít nhất một nữ A.
1
15
B.
8
15
C.
7
15
D.
1
15
Đọc tiếp
Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn có ít nhất một nữ
A. 1 15
B. 8 15
C. 7 15
D. 1 15









