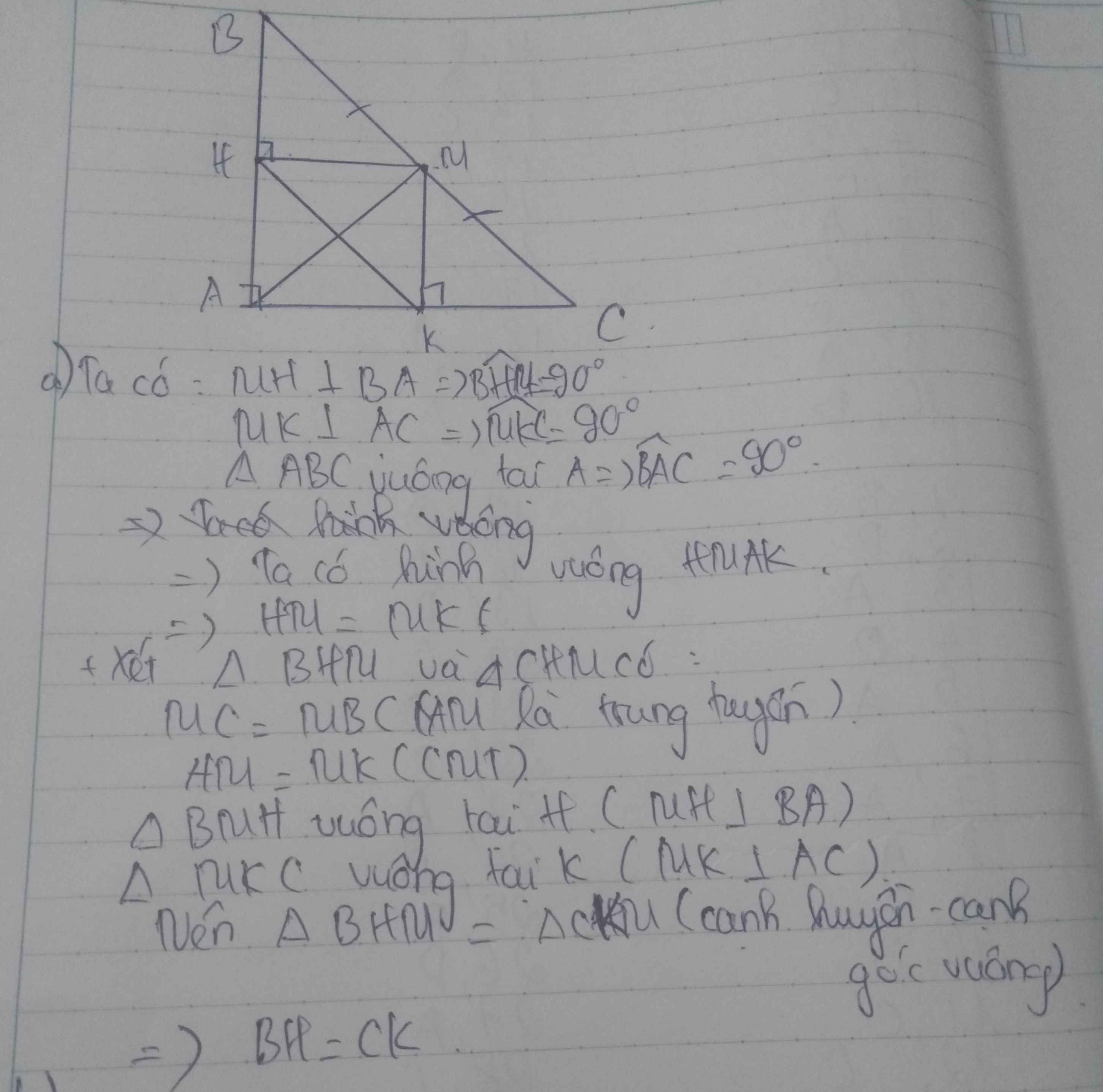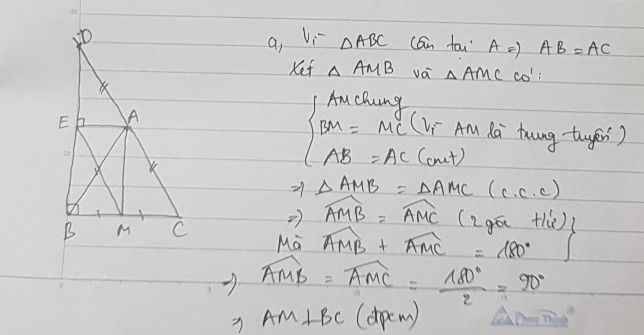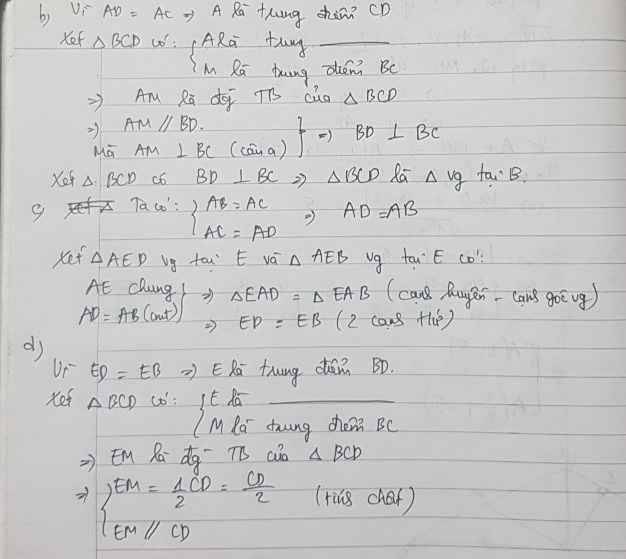cho tam giác abc vuông tại a, vẽ trung tuyến am, truung trực cd,

Những câu hỏi liên quan
cho tam giác abc vuông tại a trung tuyến am vẽ mh vuông góc với ab tại h mk vuông góc ac tại k
a chứng minh BH=CK
b chứng minh am là đường trung trực của hk
$BH=\frac{AB}{2}; CK=\frac{AC}{2}$ nên nếu $BH=CK$ thì $AB=AC$. Điều này không có trong điều kiện đề bài.
Bạn xem lại đề.
Đúng 0
Bình luận (0)
Sửa đề: ΔABC vuông cân tại A
a) Xét ΔABC có
M là trung điểm của BC(gt)
MH//AC
Do đó: H là trung điểm của AB
hay \(BH=\dfrac{AB}{2}\)(1)
Xét ΔABC có
M là trung điểm của BC(gt)
MK//AB
Do đó: K là trung điểm của AC
hay \(CK=\dfrac{AC}{2}\)(2)
Ta có: ΔABC vuông cân tại A(gt)
nên AB=AC(3)
Từ (1), (2) và (3) suy ra BH=CK
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại A có các đường trung tuyến BE và CD . Chứng minh rằng BE bằng CD
Bài 2: Cho tam giác ABC có đường trung tuyến BE và CD, biết BE = CD . Chứng minh rằng tam giác ABC cân tại A
Bài 3: Cho tam giác ABC chứng minh rằng a) Nếu tam giác ABC vuông góc tại A , có trung tuyến AM =1/2 BC
b) Nếu trung tuyến AM =1/2 BC thì tam giác ABC vuông góc tại A
cho tam giác ABC cân tại A vẽ trung tuyến AM . Từ M kẻ ME vuông góc với AB tại E , kẻ MF vuông góc với AC tại F
a, chứng minh tam giác BEM = tam giác CFM
b, chứng minh AM là đường trung trực của EF
a./ \(\Delta BEM=\Delta CFM\)vì:
góc BEM = góc CFM ( = 90o )góc EBM = góc FCM (2 góc bằng nhau của tam giác cân ABC tại A)=> góc EMB = góc FMC ( = 180o - 2 góc bằng nhau)MB = MC (vì AM là trung tuyến).b./ => ME = MF (cạnh tương ứng của 2 tam giác bằng nhau) => M nằm trên trung trực của EF (vì cách đều 2 đầu của EF) (1)
\(\Delta BEM=\Delta CFM\)=> BE = CF => AE = AF ( vì cùng bằng AB - BE = AC - CF)
=> A nằm trên trung trực của EF (vì cách đều 2 đầu của EF) (2)
Từ (1) (2) => AM là trung trực của EF.
Đúng 0
Bình luận (0)
Câu 10: Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc Với AC tại F.
a) Chứng minh ![]()
b) Chứng minh AM là trung trực của EF.
b) ta có tam giác ABC cân
=> \(\widehat{B}=\widehat{C}=180-\widehat{A}\) (1)
mà AM là trung tuyến => AM cx là phân giác và AM cx là đường cao (t/c tam giác cân)
=>\(\widehat{A1}=\widehat{A2}\)
xét tam giác AEM và tam giác AfM
có AM chung
\(\widehat{E}=\widehat{F}\)=90o
\(\widehat{A1}=\widehat{A2}\)
=> tam giác AEM =tam giác AFM (CH-GN)
=> AE =AC (2 cạnh tương ứng)
=> tam giác AEF cân ở \(\widehat{A}\)
=> \(\widehat{E}=\widehat{F}=180-\widehat{A}\) (2)
từ 1 và 2 =>\(\widehat{E}=\widehat{B}\) mà 2 góc ở vt đồng vị
=> EF // BC
mà AM ⊥ BC
=> EF ⊥ AM
=> AM là trung trực của EF (t/c tam giác cân)
Đúng 0
Bình luận (1)
b) Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
MB=MC(M là trung điểm của BC)
\(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
Do đó: ΔEMB=ΔFMC(cạnh huyền-góc nhọn)
Suy ra: ME=MF(hai cạnh tương ứng) và EB=FC(Hai cạnh tương ứng)
Ta có: AE+EB=AB(E nằm giữa A và B)
AF+FC=AC(F nằm giữa A và C)
mà EB=FC(cmt)
và AB=AC(ΔBAC cân tại A)
nên AE=AF
Ta có: AE=AF(cmt)
nên A nằm trên đường trung trực của EF(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: ME=MF(cmt)
nên M nằm trên đường trung trực của EF(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của EF(Đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có góc B = 60o. Vẽ trung tuyến AM. Kéo dài AM một đoạn MD=MA.
a/ Chứng minh CD vuông góc với CA
b/ Chứng minh ta giác ABM là tam giác đều
a, Có: AM là trung tuyến ΔABC
\(\Rightarrow\) M là trung điểm BC
\(\Rightarrow MB=MC\)
Xét ΔABM và ΔCDM có:
\(MB=MC\left(cmt\right)\)
\(\widehat{AMB}=\widehat{CMD}\left(đ^2\right)\)
\(MA=MD\)
\(\Rightarrow\) ΔABM = ΔCDM ( c.g.c )
\(\Rightarrow\widehat{BAM}=\widehat{DCM}\left(2gtu\right)\)
\(\Rightarrow AB//CD\)
Mà \(BA⊥AC\)
\(\Rightarrow DC⊥AC\)
b, Có: ΔABM = ΔCDM ( cmt )
\(\Rightarrow\left\{{}\begin{matrix}BA=DC\left(2ctu\right)\\\widehat{ABM}=\widehat{CDM}\left(2gtu\right)\end{matrix}\right.\)
Xét ΔABC và ΔCDA có:
\(\widehat{ABM}=\widehat{CDM}\left(cmt\right)\)
\(AB=CD\left(cmt\right)\)
\(\widehat{BAC}=\widehat{DCA}\left(=90^o\right)\)
\(\Rightarrow\) ΔABC = ΔCDA ( g.c.g )
\(\Rightarrow BC=DA\left(2ctu\right)\)
Có: M là trung điểm BC
M là trung điểm AD ( MA = MD )
Mà \(BC=AD\)
\(\Rightarrow MA=MB\)
\(\Rightarrow\) ΔABM cân tại M
Mà \(\widehat{ABM=60^o}\)
\(\Rightarrow\) ΔABM là tam giác đều.
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, có BC=10 cm, trung tuyến BI và AM giao nhau tại G, vẽ CD vuông góc tia BI tại D. Tính AG
AM=BC/2=5cm
Xét ΔABC có
AM,BI là trung tuyến
AM cắt BI tại G
=>G là trọng tâm
=>AG=2/3AM=2/3*5=10/3cm
Đúng 0
Bình luận (0)
cho tam giác ABC , kẻ trung tuyến AM. Ở phía ngoài tam giác ABC vẽ các tam giác vuông cân tại A là ABE và ACG .Chứng minh :
a) AB//CD(D thuộc tia đối tia MA sao cho MD=MA)
b) AM VUÔNG GÓC EG
Cho tam giác ABC vuông tại A, có góc B bằng 60 độ, vẽ đường cao AH và đường trung tuyến AM, đường tròn tâm O đường kính MC cắt AC tại D
a) Chứng minh tam giác MCD vuông
b) Chứng minh AM là đường trung trực của HD
c) Chứng minh HD là tiếp tuyến của (O)
Cho tam giác ABC cân tại A trung tuyến AM D thuộc tia đối của AC sao cho AD=AC vẽ AE vuông góc BD a) c/m AM vuông góc BC b) c/m tam giác BDC vuông ở B c) c/m EB=ED d) EM//CD
a: ΔABC cân tại A có AM là trung tuyến
nên AM vuông góc BC
b: Xét ΔDBC có
BA là trung tuyến
BA=CD/2
=>ΔDBC vuông tại B
c: ΔABD cân tại A có AE là đường cao
nên E là trung điểm của BD
d: Xét ΔDBC có BE/BD=BM/BC
nên EM//DC
Đúng 0
Bình luận (0)