hai đường thẳng xx phẩy và yy phẩy cắt nhau tại O sao cho gó xOy = 50 độ . tính số đo góc xoy phẩy

Những câu hỏi liên quan
cho đường thẳng xx phẩy cắt đường thẳng yy phẩy tại điểm O. biết xoy và xoy phẩy là 2 góc kề bù xoy phẩy =1/4 xoy .tìm số đo các góc được tạo bởi 2 đường thẳng xx phẩy cắt yy phẩy
cho hai đường thẳng xx phẩy và yy phẩy song song với nhau.Đường thẳng zz phẩy cắt hai đường thẳng xx phẩy và yy phẩy lần lượt tại Avà B.Biết góc xAB=50 độ
a/hãy vẽ hình
b/chỉ ra các cặp góc bằng nhau?vì sao?
c/tính góc ABy và góc z phẩy By phẩy
cho 2 đường thẳng xx phẩy và yy phẩy cắt nhau tại O cho biết goc xOy phẩy = 48 độ
Tìm số đo các góc xOy, x phẩy Oy, góc xOy phẩy
gọi OA là tia phân giác của góc xOy phẩy
gọi Ob là tia phân giác của góc xOy phẩy
chứng tỏ rằng góc AOB=90 độ
a/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 90 độ . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
b/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 30 độ . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
Cho 2 đường thẳng xx phẩy và yy phẩy cắt nhau tại O sao cho góc xoy=45 độ.Tính các góc khác góc bẹt còn lại trên trên hình. KHÔNG CẦN VẼ HÌNH
\(\widehat{x'Oy'}=45^o;\widehat{x'Oy}=\widehat{xOy'}=180^o-45^o=135^o\)
Đúng 0
Bình luận (0)
Bài làm
~ Mik vẽ hình thì mới làm được ~
Ta có: \(\widehat{xOy}=\widehat{x'Oy'}\)( Hai góc đối đỉnh )
Mà \(\widehat{xOy}=45^0\)
=> \(\widehat{x'Oy'}=45^0\)
Lại có: \(\widehat{x'Oy}+\widehat{xOy}=180^0\)( Hai góc kề bù )
=> \(\widehat{x'Oy}=180^0-\widehat{xOy}\)
hay \(\widehat{x'Oy}=180^0-45^0\)
=> \(\widehat{x'Oy}=135^0\)
Mà \(\widehat{x'Oy}\)là góc đối với \(\widehat{xOy'}\)
Do đó: \(\widehat{xOy'}=135^0\)
Vậy \(\widehat{x'Oy'}=45^0\)
\(\widehat{x'Oy}=135^0\)
\(\widehat{xOy'}=135^0\)
# Chúc bạn học tốt #
Đúng 0
Bình luận (0)
Vẽ hai đường thẳng xx' và yy' cắt nhau tại O sao cho xOy=60o . Tính số đo góc xOy' , x'Oy', x'Oy ?
Vì xOy và xOy' là 2 góc kề bù
=> xOy + xOy' = 180*
Thay xOy = 60*
=> xOy' = 180* - 60*
xOy' = 120*
Vì xx' và yy' cắt nhau tại O
=> xOy và x'Oy' là 2 góc đối đỉnh mà xOy = 60*
=> xOy = x'Oy' = 60*
Vì x'Oy là góc đối đỉnh của xOy' mà xOy' = 120*
=> x'Oy = 120*
Tính rõ rồi nha bạn, nếu cần chứng minh 2 góc đối đỉnh, lm đầy đủ hơn nữa thì bảo mik, cn như này là cx đc điểm tối đa òi
Đúng 1
Bình luận (0)
Ta có:
Do \(\widehat{xOy}\) và \(\widehat{xOy'}\) là 2 góc kề bù
\(\Rightarrow\)\(\widehat{xOy}\) + \(\widehat{xOy'}\) = 180o
\(\Rightarrow\)60o + \(\widehat{xOy'}\) = 180o
\(\Rightarrow\)\(\widehat{xOy'}\) = 180o - 60o = 120o
Vậy \(\widehat{xOy'}\)= 120o
Ta có:
Do \(\widehat{xOy}\)và góc \(\widehat{x'Oy'}\) là 2 góc đối đỉnh
\(\Rightarrow\)\(\widehat{xOy}=\widehat{x'Oy'}=60^o\)
Ta có:
Do \(\widehat{xOy}\) và \(\widehat{x'Oy}\) là 2 góc kề bù
\(\Rightarrow\widehat{xOy}+\widehat{x'Oy}=180^o\)
\(\Rightarrow60^o+\widehat{x'Oy}=180^o\)
\(\Rightarrow\widehat{x'Oy}=180^o-60^o=120^o\)
Vậy \(\widehat{x'Oy=120^o}\)
Hoặc bạn có thể giải bằng cách này thì ngắn gọn hơn
Ta có:
Do \(\widehat{xOy'}\) và \(\widehat{x'Oy}\) là hai góc đối đỉnh
\(\Rightarrow\widehat{xOy'}=\widehat{x'Oy}=120^o\)
Vậy \(\widehat{x'Oy}=120^o\)
Đúng 0
Bình luận (0)
cho 2 đường thẳng xx' và yy' cắt nhau tại O. góc xOy có số đo là 100 độ. tính số đo các góc tạo thành bởi 2 đường thẳng xx' và yy'?
Ta có :
`@)` `\hat{x'Oy'} = \hat{xOy} = 100^@` (hai góc đối đỉnh)
`@)` `\hat{xOy + \hat{xOy'} = 180^@`
hay `100 +` `\hat{xOy'} = 180^@`
`⇒\hat{xOy'} = 180^@ - 100^@ = 80^@`
`@)` `\hat{x'Oy} = \hat{xOy'} = 80^@` (hai góc đối đỉnh)
Đúng 5
Bình luận (0)
Ta có :
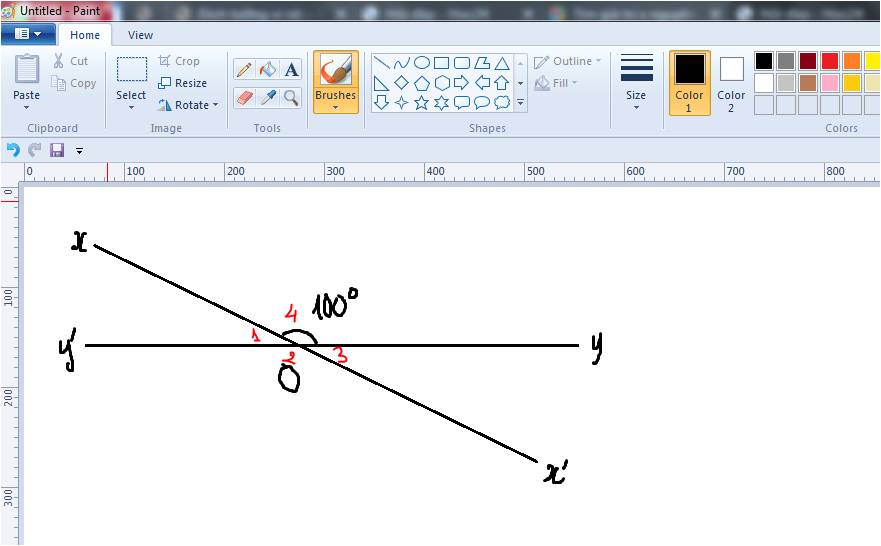
\(\widehat{O_1}=180^o-\widehat{O_4}=180^o-100^o=80^o\)
\(\widehat{O_2}=\widehat{O_4}=100^o\) (đối đỉnh)
\(\widehat{O_3}=\widehat{O_1}=80^o\) (đối đỉnh)
Đúng 4
Bình luận (0)
cho 2 đường thẳng xx' và yy' cắt nhau tại O. góc xOy có số đo là 100 độ. tính số đo các góc tạo thành bởi 2 đường thẳng xx' và yy'?
a/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 900 . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
b/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 300 . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
a ) Ta có : xOy + yOx ' = 180 ( kề bù )
\(\Rightarrow\) 90 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 90 = 90
Lại có : xOy + y ' Ox = 180 ( kề bù )
\(\Rightarrow\) 90 + y ' Ox = 180
\(\Rightarrow\) y ' Ox = 180 - 90 = 90
Ta thấy : xOy ' + y ' Ox ' = 180 ( kề bù )
\(\Rightarrow\) 90 + y ' Ox ' = 180
\(\Rightarrow\) y ' Ox ' = 180 - 90 = 90
b ) Ta có : xOy + yOx ' = 180 ( kề bù )
\(\Rightarrow\) 30 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 30 = 150
Lại có : xOy + yOx '= 180 ( kề bù )
\(\Rightarrow\) 30 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 30 = 150
Ta thấy : x ' Oy + y ' Ox ' = 180 ( kề bù )
\(\Rightarrow\) 150 + y ' Ox ' = 180
⇒ y ' Ox ' = 180 - 150 = 3
Bài làm lại :
a ) \(\widehat{xOy}+\widehat{y'Oy}=180^o\)( KB )
\(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-90^o=90^o\)( Đối đỉnh )
Vậy \(\widehat{xOy}'=\widehat{y'Ox}=90^o\)( Đối đỉnh )
b ) \(\widehat{xOy}+\widehat{x'Oy}=180^o\)( KB )
\(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-30^o=150^o\)
Vậy \(\widehat{xOy}=\widehat{x'Oy'}=30^o\)( Đối đỉnh )
\(\widehat{yOx'}=\widehat{y'Ox}=150^o\)( Đối đỉnh )
















