Cho Tam giác ABC có M trung điểm BC biểu diễn đồ thị CM và AB và AC véctơ

Những câu hỏi liên quan
Cho tam giác đều ABC cạnh a. Trên ba cạnh AB, BC, CA lần lượt lấy các điểm M, N, P sao cho véctơ BM = 1/2véctơ BA, véctơ BN = 1/3véctơ BC, véctơ AP = 5/8véctơ AC
a) Tính tích véctơ AB x véctơ CA
b) Biểu thị hai véctơ MP, AN theo hai véctơ AB, AC. Chứng minh MP vuông góc AN
Cho tam giác đều ABC cạnh a. Trên ba cạnh AB, BC, CA lần lượt lấy các điểm M, N, P sao cho véctơ BM = 1/2véctơ BA, véctơ BN = 1/3véctơ BC, véctơ AP = 5/8véctơ AC
a) Tính tích véctơ AB x véctơ CA
b) Biểu thị hai véctơ MP, AN theo hai véctơ AB, AC. Chứng minh MP vuông góc AN
Cho tam giác đều ABC cạnh a. Trên ba cạnh AB, BC, CA lần lượt lấy các điểm M, N, P sao cho véctơ BM = 1/2véctơ BA, véctơ BN = 1/3véctơ BC, véctơ AP = 5/8véctơ AC
a) Tính tích véctơ AB x véctơ CA
b) Biểu thị hai véctơ MP, AN theo hai véctơ AB, AC. Chứng minh MP vuông góc AN
Ai làm được mình cho kb facebook hi <3
1 ) cho tam giác ABC có AB=AC . trên các cạnh AB,AC lần lượt lấy các điểm E và F sao cho AE = AF
cm : AF // BC
2) cho tam giác ABC có M và N lần lượt là trung điểm của AB , AC
cm : MN // BC và MN = 1 phần 3 BC
cho tam giác ABC có góc A=90 độ;AB<AC. gọi M là trung điểm của BC trên tia đối của tia MA lấy E sao cho MA=ME.
a) cm AB=EC VÀ AB // EC
b) cm tam giác ACE vuông tại C
c)cm tam giác ABC và TAM GIÁC CEA
D) CM AM=1/2 BC
E) CM AC=BE VÀ AC // BC
F)TRÊN BE lấy K, trên AClấy H sao cho BK=CH. CM 3 ĐIỂM K,M,H THẲNG HÀNG
a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMEC
=>AB=EC
Ta có: ΔMAB=ΔMEC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE
b: Ta có: AB//CE
AB\(\perp\)AC
Do đó: CE\(\perp\)CA
=>ΔCAE vuông tại C
c: Xét ΔABC vuông tại A và ΔCEA vuông tại C có
CA chung
AB=CE
Do đó: ΔABC=ΔCEA
d: ta có: ΔABC=ΔCEA
=>BC=EA
mà \(AM=\dfrac{1}{2}EA\)
nên \(AM=\dfrac{1}{2}BC\)
e: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BE
f: Xét ΔMHC và ΔMKB có
MB=MC
\(\widehat{MBK}=\widehat{MCH}\)
BK=CH
Do đó: ΔMHC=ΔMKB
=>\(\widehat{HMC}=\widehat{KMB}\)
mà \(\widehat{KMB}+\widehat{KMC}=180^0\)(hai góc kề bù)
nên \(\widehat{HMC}+\widehat{KMC}=180^0\)
=>K,M,H thẳng hàng
Đúng 2
Bình luận (0)
a) Ta có M là trung điểm của BC, vậy BM = MC. Vì MA = ME, nên ta có MA = ME = MC. Do đó, tam giác MEC là tam giác đều.
Vì BM = MC và tam giác MEC là tam giác đều, nên ta có AB = EC và AB // EC.
b) Vì tam giác ABC là tam giác vuông tại A, nên góc BAC = 90 độ.
Vì AB // EC, nên góc BAC = góc ECA.
Vậy tam giác ACE cũng là tam giác vuông tại C.
c) Tam giác ABC và tam giác CEA có cạnh chung AC và góc AEC = góc BAC = 90 độ (vì tam giác ABC là tam giác vuông tại A).
Vậy theo trường hợp góc - cạnh - góc, ta có tam giác ABC và tam giác CEA là hai tam giác đồng dạng.
d) Ta đã biết M là trung điểm của BC, vậy BM = MC.
Vì MA = ME, nên MA = MC/2.
Do đó, AM = 1/2 BC.
e) Ta đã biết AB = EC và AB // EC.
Vì MA = ME, nên MA = MC.
Vậy theo trường hợp cạnh - góc - cạnh, ta có tam giác MAC và tam giác MEC là hai tam giác đồng dạng.
Vậy AC = BE và AC // BC.
f) Trên BE lấy K, trên AC lấy H sao cho BK = CH.
Vì M là trung điểm của BC, nên MK = MC/2.
Vì tam giác MEC là tam giác đều, nên góc MCE = 60 độ.
Vậy góc MCK = 60 độ.
Vì BK = CH, nên góc BKC = góc CHB.
Vậy góc BKC = góc CHB = 60 độ.
Vậy tam giác BKC và tam giác CHB là hai tam giác đều.
Vậy 3 điểm K, M, H thẳng hàng.
Đúng 1
Bình luận (0)
Giải giúp mik vs ạ
Thank you ♥️
Cho tam giác ABC có AB = 12cm, AC = 16 cm, BC = 20 cm. 1. Tam giác ABC là tam giác gì? 2. Lấy M, N lần lượt trên AB, AC sao cho AM = 3cm, AN = 4cm. CMR: MN // BC 3. Gọi I là trung điểm BC. G là giao điểm của AI và MN. CMR: G là trung điểm MN
Cho tam giác ABC có AB 2, AC 4,
A
^
60
°
. M và N lần lượt là trung điểm của AB và AC. Biểu thức
B
N
→
.
C
M
→
bằng A.5 B. -5 C. 7 D. -7
Đọc tiếp
Cho tam giác ABC có AB = 2, AC = 4, A ^ = 60 ° . M và N lần lượt là trung điểm của AB và AC. Biểu thức B N → . C M → bằng
A.5
B. -5
C. 7
D. -7
A B → . A C → = A B . A C . cos A = 2.4. cos 60 ° = 2.4. 1 2 = 4 , A B → 2 = 4 , A C → 2 = 16
B N → . C M → = A N → − A B → . A M → − A C → = 1 2 A C → − A B → . 1 2 A B → − A C →
= 1 4 A C → . A B → − 1 2 A B → 2 − 1 2 A C → 2 + A C → . A B → = 5 4 A C → . A B → − 1 2 A B → 2 − 1 2 A C → 2
= 5 4 .4 − 1 2 .4 − 1 2 .16 = − 5
Chọn B
Đúng 0
Bình luận (0)
Bài 1. Cho tam giác ABC có AB cm 16 , BC cm 20 và AC cm 12 . a) Chứng minh : ABC vuông tại A . b) Gọi M là trung điểm của BC . KẻMFAC tại F . Chứng minh :FA FC . c) Gọi E là trung điểm của AB . Chứng minh : ME AB và tính độdài ME . Bài 2. Cho hình thang ABCD có hai đáy là AB và CD . Gọi E, F, K lần lượt là trung điểm các cạnh AD, BC, BD . a) Chứng minh: EK // AB ; KF // AB và E, F, K thẳng hàng. b) Gọi I là giao điểm EF và AC . Chứng minh : IA IC . c) Chứng minh : IE KF và KE IF. d) Ch...
Đọc tiếp
Bài 1. Cho tam giác ABC có AB cm 16 , BC cm 20 và AC cm 12 . a) Chứng minh : ABC vuông tại A . b) Gọi M là trung điểm của BC . KẻMFAC tại F . Chứng minh :FA = FC . c) Gọi E là trung điểm của AB . Chứng minh : ME AB và tính độdài ME . Bài 2. Cho hình thang ABCD có hai đáy là AB và CD . Gọi E, F, K lần lượt là trung điểm các cạnh AD, BC, BD . a) Chứng minh: EK // AB ; KF // AB và E, F, K thẳng hàng. b) Gọi I là giao điểm EF và AC . Chứng minh : IA = IC . c) Chứng minh : IE = KF và KE = IF. d) Cho biết AB 6 cm ; CD 10 cm . Tính IK.
cho tam giác abc vuông cân tại a có ab=8 cm, ac=6 cm, gọi M là trung điểm của BC. a) cmr: ac và đường tròn ( M;4 cm) tiếp xúc nhau B) cmr: ab và đường tròn tâm (M;4 cm) cắt nhau tại 2 điểm D, E. tính ad và be
Cho tam giác ABC có M là trung điểm AC, N là trung điểm BC và AB = a. Tính độ dài vecto \(\overrightarrow {CM} - \overrightarrow {NB} \).
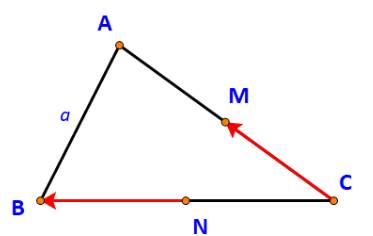
Ta có: \(\overrightarrow {NB} \) và \(\overrightarrow {NC} \) là hai vecto đối nhau (do N là trung điểm của BC)
\( \Rightarrow \overrightarrow {NC} = - \overrightarrow {NB} \)
Do đó: \(\overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {CM} + \overrightarrow {NC} = \overrightarrow {NC} + \overrightarrow {CM} \)(tính chất giáo hoán)
\( \Rightarrow \overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {NM} \Leftrightarrow \;|\overrightarrow {CM} - \overrightarrow {NB} |\, = \;|\overrightarrow {NM} | = NM.\)
Vì: M, N lần lượt là trung điểm của AC, BC nên \(MN = \frac{1}{2}AB = \frac{a}{2}.\)
Vậy \(\;|\overrightarrow {CM} - \overrightarrow {NB} |\, = \frac{a}{2}.\)
Đúng 0
Bình luận (0)















