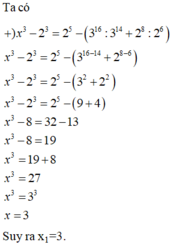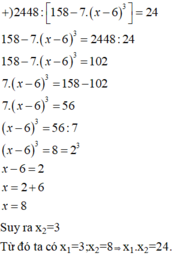x2.x3=28:23

Những câu hỏi liên quan
Cho
x
1
là số thỏa mãn
x
3
-
2
3
2
5
-
3
16
:
3
14
+
2
8
:
2
6
và
x
2
là số thỏa m...
Đọc tiếp
Cho x 1 là số thỏa mãn x 3 - 2 3 = 2 5 - 3 16 : 3 14 + 2 8 : 2 6 và x 2 là số thỏa mãn 2448 : 158 - 7 . x - 6 3 = 24 . Tính x 1 . x 2
A. 3
B. 11
C. 8
D. 24
Bài 1: Khai triển các hằng đẳng thức.
1,(x+1)2
2,(2x+1)2
3, (2x+y)2
4, (2x+3)2
5, ( 3x+2y)2
6, (2x2+1)2
7, (x3+1)2
8, (x2+y3)2
9, ( x2+2y2)2
10, (1/2x+1/3y)2
1) \(\left(x+1\right)^2=x^2+2x+1\)
2) \(\left(2x+1\right)^2=4x^2+4x+1\)
3) \(\left(2x+y\right)^2=4x^2+4xy+y^2\)
4) \(\left(2x+3\right)^2=4x^2+12x+9\)
5) \(\left(3x+2y\right)^2=9x^2+12xy+4y^2\)
6) \(\left(2x^2+1\right)^2=4x^4+4x^2+1\)
7) \(\left(x^3+1\right)^2=x^6+2x^3+1\)
8) \(\left(x^2+y^3\right)^2=x^4+2x^2y^3+y^6\)
9) \(\left(x^2+2y^2\right)^2=x^4+4x^2y^2+4y^4\)
10) \(\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^2=\dfrac{1}{4}x^2+\dfrac{1}{3}xy+\dfrac{1}{9}y^2\)
Đúng 1
Bình luận (0)
Giải các phương trình sau:a)
1
−
x
2
+
x
+
2
2
2
x
x
−
3
−
7
;
b)
2
−
x...
Đọc tiếp
Giải các phương trình sau:
a) 1 − x 2 + x + 2 2 = 2 x x − 3 − 7 ;
b) 2 − x 3 − x − 4 3 = 8 x − 3 2 ;
c) 3 x − 1 4 + 6 x − 2 8 = 1 − 3 x 6 ;
d) x + 2 3 − x 5 12 = 1 + 1 − 9 − 2 x 12 5 .
a) Triển khai hằng đẳng thức và rút gọn được 8x + 12 = 0
Từ đó tìm được x = - 3 2
b) Sử dụng hằng đẳng thức, biến đổi phương trình về dạng: (x - 3)(2 x 2 - 4x) = 0
Sưe dụng phương pháp giải PT tích tìm được x ∈ {0; 2; 3}
c) Quy đồng khử mẫu ta được 48x - 16 = 0
Từ đó tìm được x = 1 3
d) Quy đồng khử mẫu ta được 3x + 6 = 2x + 63
Từ đó tìm được x = 57.
Đúng 0
Bình luận (0)
1. Tìm x ∈ N sao cho:
a) (x - 140) : 7 = 33 - 23 . 3
b) x3 . x2 = 28 : 23
c) (x + 2) . (x - 4) = 0
d) 3x-3 - 32 = 2 . 32
2. Tìm x ∈ N sao cho:
a) 9 : (x + 2)
b) (x + 17) : (x + 3)
Giúp mình với, mình cân gấp!
a) (x - 140) : 7 = 33 - 23 . 3
(x - 140) : 7 = 27 - 8 . 3 = 27 - 24 = 3
x - 140 = 3 x 7 = 21
x = 21 + 140 = 161
b) x3 . x2 = 28 : 23
x5 = 25
=> x = 2
c) (x + 2) . ( x - 4) = 0
x = -2 hoặc 4
d) 3x-3 - 32 = 2 . 32 =
3x-3 - 9 = 2 . 9 = 18
3x-3 = 18 + 9 = 27
3x-3 = 33
=> x - 3 = 3
x = 3 + 3 = 6
Đúng 1
Bình luận (1)
2.
a) 9 : ( x + 2 )
9 ⋮ 1 ; 9 ⋮ 3 ; 9 ⋮ 9
=> x = -1 ; 1 ; 7
Đúng 1
Bình luận (1)
Rút gọn biểu thức x3(x+2) – x(x3 + 23) – 2x(x2 – 22)
Ta có:
x3(x+2) – x(x3 + 23) – 2x(x2 – 22)
= x3 . x + x3 . 2 – (x . x3 + x . 23) – ( 2x . x2 – 2x . 22)
= x4 + 2x3 – (x4 + 8x ) – (2x3 – 8x)
= x4 + 2x3 – x4 – 8x – 2x3 + 8x
= (x4 – x4) + (2x3 – 2x3) + (-8x + 8x)
= 0
Đúng 0
Bình luận (0)
123 - 23 x 1 x3 x2
Số cần tìm là :
123 - 23 * 1 * 3 * 2 = - 15
Đ / S : -15
Ai tích mình mình tích lại
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình :
x
3
−
4
3
(
x
2
+
4
)
2
3
+
4...
Đọc tiếp
Giải phương trình : x 3 − 4 3 = ( x 2 + 4 ) 2 3 + 4 2 .
ĐK: x > 4 3
Đặt: x 3 − 4 = u 2 x 2 + 4 3 = v ( v > 1 ) ⇒ v 3 − 4 = x 2
Khi đó phương trình (1) ⇔ u 2 3 = v 2 + 4 2 hay u 3 − 4 = v 2 (4)
Từ (2), (3), (4) ta có hệ phương trình:
x 3 − 4 = u 2 v 3 − 4 = x 2 u 3 − 4 = v 2 ⇒ x 3 − v 3 = u 2 − x 2 ( 5 ) u 3 − x 3 = v 2 − u 2 ( 6 )
Vì x, u, v > 1 nên giả sử x ≥ v thì từ (5) ⇒ u ≥ x
Có u ≥ x nên từ (6) ⇒ v ≥ u
Do đó: x ≥ v ≥ u ≥ x ⇒ x = v = u
Mặt khác, nếu x < v thì tương tự ta có x < v < u < x (vô lí)
Vì x = u nên:
x 3 − 4 = x 2 ⇔ x − 2 x 2 + x + 2 = 0 ⇔ x = 2 (thỏa mãn)
Vậy phương trình (1) có nghiệm duy nhất x = 2.
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:
1) x2 - y2 - 2x + 1
2) x3 - 2x2 - x + 2
3) x2 - 2x2 - x + 2
1: =(x-1-y)(x-1+y)
3: =(x-1)(x+1)(x-2)
Đúng 1
Bình luận (0)
Giải phương trình :
1) √x2+x+2 + 1/x= 13-7x/2
2) x2 + 3x = √1-x + 1/4
3) ( x+3)√48-x2-8x= 28-x/ x+3
4) √-x2-2x +48= 28-x/x+3
5) 3x2 + 2(x-1)√2x2-3x +1= 5x + 2
6) 4x2 +(8x - 4)√x -1 = 3x+2√2x2 +5x-3
7) x3/ √16-x2 + x2 -16 = 0
Một vật tham gia đồng thời ba dao động điều hoà cùng phương:
x
1
2
cos
ω
t
c
m
,
x
2
2
cos
ω
t
+
φ
2
c
m...
Đọc tiếp
Một vật tham gia đồng thời ba dao động điều hoà cùng phương: x 1 = 2 cos ω t c m , x 2 = 2 cos ω t + φ 2 c m và x 3 = 2 cos ω t + φ 3 c m v ớ i φ 3 ≠ φ 2 và 0 ≤ φ 3 , φ 2 ≤ π Dao động tổng hợp của x 1 v à x 2 có biên độ là 2 cm, dao động tổng hợp của x 1 v à x 3 có biên độ là 2 3 c m . Độ lệch pha giữa hai dao động x 2 v à x 3 là
A. 5 π / 6
B. π / 3
C. π / 2
D. 2 π / 3
Hướng dẫn: Chọn đáp án B

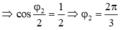
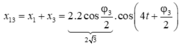
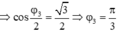
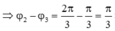
=> Chọn B
Chú ý: Khi cho biết A, j1, j2 tìm điều kiện để A1 max hoặc A2 max ta viết lại hệ thức:
![]()
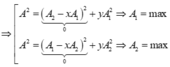
Đúng 0
Bình luận (0)