Cho tam giác ABC vuông tại A có góc C=30 độ.Trên cạnh BC lấy điểm M sao cho BM=BA.Chứng minh rằng:
a)Tam giác ABM đều. b) AM=BC/2.
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có góc C=30°. Trên cạnh BC lấy 2 điểm M và N sao cho BM=BA
a, Tính số đo góc B cm tam giác AMB đều
b, Tính góc MAC. Tam giác AMC là tam giác gì vì sao
c, chứng minh AM=1/2
Cho tam giác cân ABC(BA=BC),B=80 độ.Trên nửa mặt phẳng chứa điểm A có bờ là BC vẽ tia Bx sao cho CBx=10 độ.Trên tia Bx lấy E sao cho AE=AB.Trong tam giác ABE dựng tam giác đều MBE.
a, Chứng minh tam giác ABM=tam giác AEM
b, tính số đo góc BEC
c,chứng minh CE vuông góc với BM
Bài 4. Cho tam giác ABC vuông tại A có C = 30 deg Trên cạnh BC lấy điểm M sao cho BM = BA. Chứng minh rằng: a) tâm giác AMB đều. b) AM = (BC)/2 c) Kẻ phân giác của góc AMC cắt Ac tại D. CM:AB//MD.
a: Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-30^0=60^0\)
Xét ΔBAM có BA=BM và \(\widehat{ABM}=60^0\)
nên ΔBAM đều
b: Ta có: ΔMAB đều
=>\(\widehat{MAB}=60^0\)
Ta có: \(\widehat{MAB}+\widehat{MAC}=\widehat{BAC}\)
=>\(\widehat{MAC}+60^0=90^0\)
=>\(\widehat{MAC}=30^0\)
Xét ΔMAC có \(\widehat{MAC}=\widehat{MCA}\left(=30^0\right)\)
nên ΔMAC cân tại M
=>MA=MC
mà MB=MA
nên MB=MC
=>M là trung điểm của BC
=>\(AM=MB=\dfrac{1}{2}BC\)
c: Ta có: ΔMAC cân tại M
mà MD là đường phân giác
nên MD\(\perp\)AC
Ta có: MD\(\perp\)AC
AB\(\perp\)AC
Do đó: MD//AB
Đúng 3
Bình luận (0)
Cho tam giác ABC có BA<BC và góc B=60 độ
a) Trên BC lấy điểm M sao cho BM=BA.Chứng minh tam giác ABM đều
b) Tia phân giác góc B cắt Ac tại D. Chứng minh tam BAD=BMD
c) Tia MD cắt tia BA tại H, chứng minh tam giác DHC cân
Cho tam giác ABC có BA<BC và góc B=60 độ
a) Trên BC lấy điểm M sao cho BM=BA.Chứng minh tam giác ABM đều
b) Tia phân giác góc B cắt Ac tại D. Chứng minh tam BAD=BMD
c) Tia MD cắt tia BA tại H, chứng minh tam giác DHC cân
Ta có BA=BM (gt)
^B=60 độ
=>ΔABM là Δ đều
Đúng 1
Bình luận (0)
xét ΔBAD và ΔBMD
có AB=BM
^ABD=^MBD
BD chnsg
suy ra ΔBAD =ΔBMD
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có C=30°.Tia phân giác góc B cắt AC tại D.Trên cạnh BC lấy điểm M sao cho BM=BA
a) CM : tam giác ABD=tam giác MBD
b) CM: tam giác ABM là tam giác đều
c) CM : tam giác AMC là tam giác cân
d) Trên tia đối của tia AB lấy điểm E sao cho AB=AE. CM: AM//AC
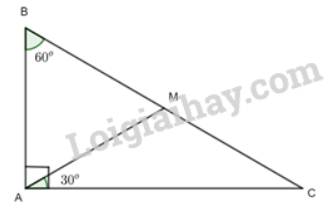
Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng:
a) Tam giác CAM cân tại M;
b) Tam giác BAM là tam giác đều;
c) M là trung điểm của đoạn thẳng BC.
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Do đó, MB = MC. Mà M nằm giữa B và C
=> M là trung điểm của BC.
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=AC=10cm,góc BAC=60 độ.Trên tia BC lấy điểm N,trên tia CB lấy điểm M sao cho BM=BC=BN.Kẻ BE vuông góc AM tại E và CF vuông góc AN tại F.Gọi I là giao điểm BE và CF.
a)Chứng minh tam giác BIC đều.
b)Tính AF biết IF=16cm
Trên tia BC lấy điểm N,trên tia BC lấy điểm M sao cho BM=BC=BN là sao hả bạn
xem lại đề bài nhé làm sao lại bằng BC được ??
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,có góc C =30 độ.trên cạnh BC lấy điểm D sao cho BD=BA a,CM.tam giác ABD là tam giác đều b.qua D kẻ DE vuông góc với BC. E thuộc AC.CM BE là phân giác của góc ABC
