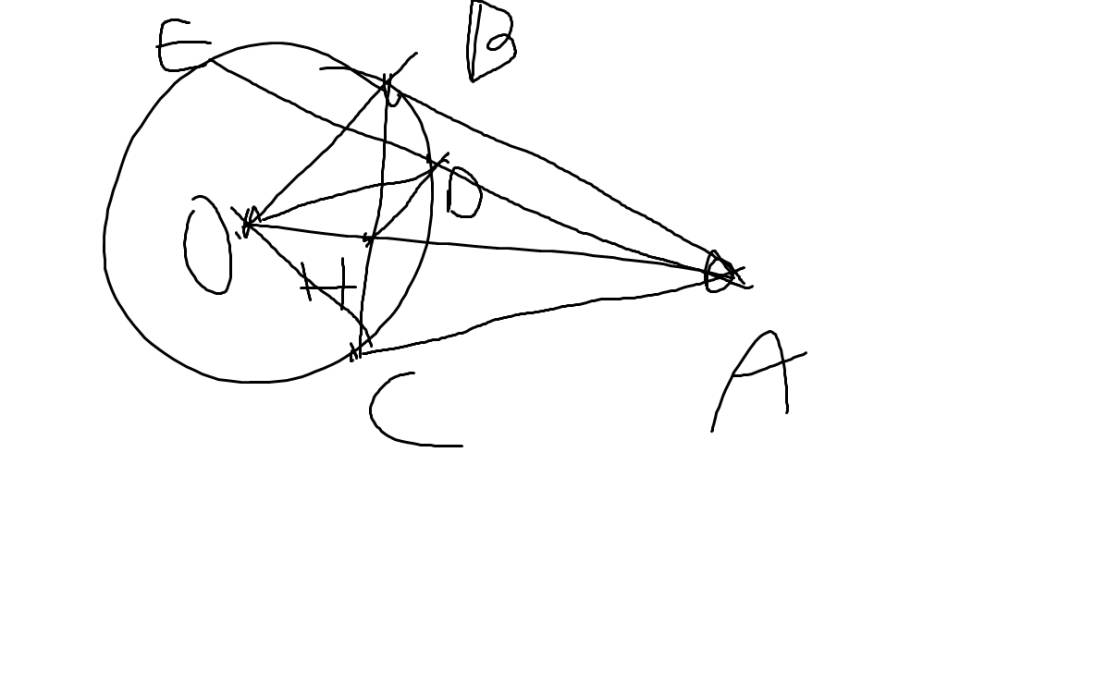
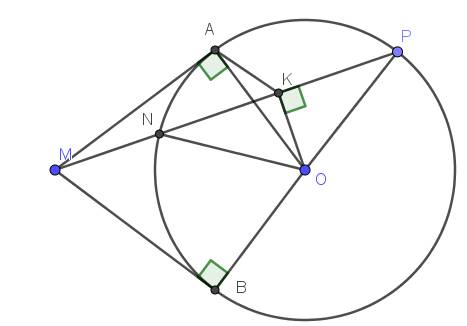
từ điểm A ở ngoài đường tròn (O;R) kẻ hai tiếp tuyến AB, AC vẽ đường kính CD. C/m BD//OA (bằng 2 cách) Giúp minh bài này với

Những câu hỏi liên quan
cho đường tròn (O;R) và đường thẳng a ở ngoài đường thẳng a ở ngoài đường tròn. Gọi OH là khoảng cách từ tâm O đếna và M là một điểm chuyển động trên a. Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (O) , (A,B là 2 tiếp điểm). Gọi D là giao điểm của AB với OH.CMR D là điểm cố định
Trả lời :
Bn Nguyễn Tũn bảo dễ ẹt thì làm đi.
- Hok tốt !
^_^
dễ ẹc thì lm cho mk coi đi
mk ko bt lm
Cho đường tròn O từ điểm A bên ngoài đường tròn, kẽ tiếp tuyến AB, AC đường thẳng qua C // AB cắt đường tròn ở D, AD cắt đường tròn O ở M, CM cắt AB ở N a, góc BAD = góc ACN b, AN2 = NM* NC
a: góc ACN=1/2*sđ cung MC
góc BAD=góc MDC=1/2*sđ cung MC
=>góc ACN=góc BAD
b: Xét ΔNAM và ΔNCA có
góc NAM=góc NCA
góc N chung
=>ΔNAM đồng dạng với ΔNCA
=>NA/NC=NM/NA
=>NA^2=NM*NC
Đúng 0
Bình luận (0)
Từ một điểm a ở bên ngoài đường tròn tâm O,kẻ hai tiếp tuyến AB,AC với đường tròn này
cho đường tròn(o;r), từ điểm a ở bên ngoài đường tròn kẻ 2 tiếp tuyến ab, ac với đường tròn(o) (b,c là tiếp điểm) từ b kẻ đường thẳng song song ac cắt đường tròn(o) tại d(d khác b), đường thẳng ad cắt đường tròn (o) tại e( e khác d) a) chứng minh tứ giác aboc nội tiếp b) chứng minh ab²= ae×ad c) giả sử oa=2r. Tính góc bec và diện tích obac d) so sánh góc cea và góc bec
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 1
Bình luận (0)
Cho đường tròn (O). Từ điểm A bên ngoài đường tròn vẽ 2 tiếp tuyến AB ,AC với đường tròn (B,C là các tiếp điểm).Đường thẳng kẻ qua C song song với AB cắt đường tròn (O) ở D ,AD cắt (O) ở M ,CM cắt AB ở N. Chứng minh:
a) Góc BAD=góc ACN
b)\(^{AN^{ }2}\)=NM.NC
C)N là trung điểm của AB.
Từ điểm A ở bên ngoài đường tròn (O), kẻ 2 tiếp tuyến AB và AC đến đường tròn (O) (B, C là tiếp điểm). Kẻ cát tuyến ADE vs đường tròn (O) (D nằm giữa A và E).
a) Cm: 4 điểm A, B, O, C cùng thuộc một đường tròn
b) Cm OA ⊥ BC tại H và OD² = OH × OA. Từ đó suy ra tam giác OHD đồng dạng vs tam giác ODA.
Giải và vẽ hình giúp mình vớiii !! :(
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,C,O cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
mà OB=OD
nên \(OD^2=OH\cdot OA\)
=>\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
Xét ΔODA và ΔOHD có
\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
\(\widehat{DOA}\) chung
Do đó: ΔODA đồng dạng với ΔOHD
Đúng 1
Bình luận (0)
Từ điểm A ở ngoài đường tròn (O), kẻ 2 tiếp tuyến AB, AC đến đường tròn (O) (B, C là tiếp điểm). Kẻ cát tuyến ADE với đường tròn (O) (D nằm giữa A và E).
a) Cm: 4 điểm A, B, O, C cùng thuộc một đường tròn
b) Cm OA ⊥ BC tại H và OD² = OH × OA. Từ đó suy ra tam giác OHD đồng dạng với tam giác ODA.
--> Cần hình vẽ ạ! (Bài giải e làm r)
Từ điểm M ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến MA, MB và cát tuyến MNP tới
đường tròn (O); gọi K là trung điểm của NP. Chứng minh rằng: 5 điểm M, A, O, K, B cùng thuộc
1 đường tròn
Lời giải:
Vì $MA,MB$ là tiếp tuyến của $O$ nên $MA\perp OA, MB\perp OB$
$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$
Xét tứ giác $MAOB$ có $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$. Mà 2 góc này đối nhau nên $MAOB$ là tứ giác nội tiếp.
$\Rightarrow M, A,O,B$ cùng thuộc 1 đường tròn (1)
Mặt khác:
Tam giác $ONP$ cân tại $O$ (do $ON=OP=R$) nên trung tuyến $OK$ đồng thời là đường cao.
$\Rightarrow \widehat{MKO}=90^0$
Xét tứ giác $MAKO$ có $\widehat{MAO}=\widehat{MKO}=90^0$. Mà 2 góc này cùng nhìn cạnh $MO$ nên $MAKO$ là tứ giác nội tiếp.
$\Rightarrow M,A,K,O$ cùng thuộc 1 đường tròn (2)
Từ $(1); (2)\Rightarrow M, A, O, K,B$ cùng thuộc 1 đường tròn.
Đúng 0
Bình luận (0)
Từ điểm M ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến MA, MB và cát tuyến MNP tới
đường tròn (O); gọi K là trung điểm của NP. Chứng minh rằng: 5 điểm M, A, O, K, B cùng thuộc
1 đường tròn
Lời giải:
Vì $MA,MB$ là tiếp tuyến của $O$ nên $MA\perp OA, MB\perp OB$
$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$
Xét tứ giác $MAOB$ có $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$. Mà 2 góc này đối nhau nên $MAOB$ là tứ giác nội tiếp.
$\Rightarrow M, A,O,B$ cùng thuộc 1 đường tròn (1)
Mặt khác:
Tam giác $ONP$ cân tại $O$ (do $ON=OP=R$) nên trung tuyến $OK$ đồng thời là đường cao.
$\Rightarrow \widehat{MKO}=90^0$
Xét tứ giác $MAKO$ có $\widehat{MAO}=\widehat{MKO}=90^0$. Mà 2 góc này cùng nhìn cạnh $MO$ nên $MAKO$ là tứ giác nội tiếp.
$\Rightarrow M,A,K,O$ cùng thuộc 1 đường tròn (2)
Từ $(1); (2)\Rightarrow M, A, O, K,B$ cùng thuộc 1 đường tròn.
Đúng 1
Bình luận (0)
Bài 6: (2,5 điểm) Từ điểm A ở ngoài đường tròn (O; R) kẻ tiếp tuyến AB (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). Đoạn AC cắt đường tròn (O) tại điểm D (khác C). a) Chứng minh tam giác BDC vuông và . AC A * B ^ 2 A * O ^ 2 - R ^ 2
b) Qua B kẻ đường thẳng d vuông góc với AO tại H. Đường thẳng d cắt đường tròn (O) tại E (khác B). Gọi F là điểm đối xứng của H qua O. Chứng minh tứ giác CEHF là hình chữ nhật và AE là tiếp tuyến của đường tròn (O; R)
c) Tia CH cắt đường tròn (O) tại G....
Đọc tiếp
Bài 6: (2,5 điểm) Từ điểm A ở ngoài đường tròn (O; R) kẻ tiếp tuyến AB (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). Đoạn AC cắt đường tròn (O) tại điểm D (khác C). a) Chứng minh tam giác BDC vuông và . AC = A * B ^ 2 = A * O ^ 2 - R ^ 2 b) Qua B kẻ đường thẳng d vuông góc với AO tại H. Đường thẳng d cắt đường tròn (O) tại E (khác B). Gọi F là điểm đối xứng của H qua O. Chứng minh tứ giác CEHF là hình chữ nhật và AE là tiếp tuyến của đường tròn (O; R) c) Tia CH cắt đường tròn (O) tại G. Chứng minh HA .HO=HG.HC. Suy ra góc GAB bằng góc EAD
a:
Sửa đề: \(AD\cdot AC=AB^2=AO^2-R^2\)
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)DC tại D
=>BD\(\perp\)CA tại D
Xét ΔBCA vuông tại B có BD là đường cao
nên \(AD\cdot AC=AB^2\left(1\right)\)
Xét ΔOBA vuông tại B có \(OB^2+BA^2=OA^2\)
=>\(BA^2+R^2=OA^2\)
=>\(BA^2=OA^2-R^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AC=AB^2=OA^2-R^2\)
b: ΔOBE cân tại O
mà OH là đường cao
nên H là trung điểm của BE
Xét ΔBCE có
O,H lần lượt là trung điểm của BC,BE
=>OH là đường trung bình của ΔBCE
=>OH//CE và OH=1/2CE
OH//CE
F\(\in\)OH
Do đó: HF//CE
\(OH=\dfrac{1}{2}CE\)
\(OH=\dfrac{1}{2}FH\)
Do đó: CE=FH
Xét tứ giác CEHF có
CE//HF
CE=HF
Do đó: CEHF là hình bình hành
Hình bình hành CEHF có \(\widehat{FHE}=90^0\)
nên CEHF là hình chữ nhật
ΔOBE cân tại O
mà OH là đường cao
nên OH là phân giác của góc BOE
Xét ΔOBA và ΔOEA có
OB=OE
\(\widehat{BOA}=\widehat{EOA}\)
OA chung
Do đó: ΔOBA=ΔOEA
=>\(\widehat{OBA}=\widehat{OEA}=90^0\)
=>AE là tiếp tuyến của (O)
c: Xét (O) có
ΔBGC nội tiếp
BC là đường kính
Do đó: ΔBGC vuông tại G
=>GB\(\perp\)GC tại G
Xét ΔHEC vuông tại E và ΔHGB vuông tại G có
\(\widehat{EHC}=\widehat{GHB}\)
Do đó: ΔHEC đồng dạng với ΔHGB
=>\(\dfrac{HE}{HG}=\dfrac{HC}{HB}\)
=>\(HE\cdot HB=HG\cdot HC\)
=>\(HG\cdot HC=HB^2\left(3\right)\)
Xét ΔBOA vuông tại B có BH là đường cao
nên \(HO\cdot HA=HB^2\left(4\right)\)
Từ (3) và (4) suy ra \(HG\cdot HC=HO\cdot HA\)
Đúng 1
Bình luận (0)