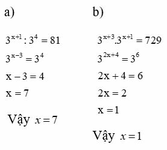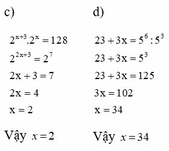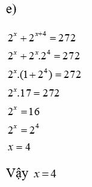3.3x-1-5=22

Những câu hỏi liên quan
bài 1: Tìm x biếta) 2.x+(-5)-18b) 3.3x−2x−281c) 64-4.(5-x)40
Đọc tiếp
bài 1: Tìm x biết
a) 2.x+(-5)=-18
b) 3.3=81
c) 64-4.(5-x)=40
a: =>2x=-18+5=-13
=>x=-13/2
b: =>3^x-1=81
=>x-1=4
=>x=5
c: =>4(5-x)=24
=>5-x=6
=>x=-1
Đúng 0
Bình luận (0)
2/3.3x+1 - 7.3x = -405
\(\dfrac{2}{3}\cdot3^{x+1}-7\cdot3^x=-405\)
\(\Rightarrow3^x\cdot\left(\dfrac{2}{3}\cdot3-7\right)=-405\)
\(\Rightarrow3^x\cdot\left(2-7\right)=-405\)
\(\Rightarrow3^x\cdot-5=-405\)
\(\Rightarrow3^x=-405:-5\)
\(\Rightarrow3^x=81\)
\(\Rightarrow3^x=3^4\)
\(\Rightarrow x=4\)
Vậy: \(x=4\)
Đúng 1
Bình luận (0)
\(\Leftrightarrow3\cdot\dfrac{2}{3}\cdot3^x-7\cdot3^x=-405\)
=>\(-5\cdot3^x=-405\)
=>3^x=81
=>x=4
Đúng 1
Bình luận (0)
75%.(7/3x+2/3x-5/4)=1
1/4+1/3.3x=5
7/3-(5/4x+1tren 1/2)=2/5
giup mình với
Tìm x nguyên để
B= 2x+3.3x-5 là số dương
Help me
Mk đang cần gấp
\(B=2x+3.3x-5\)
\(=2x+9x-5\)
\(=11x-5\)
\(\)Để \(B\ge0\Leftrightarrow11x-5\ge0\)
\(\Leftrightarrow11x\ge5\)
\(\Leftrightarrow x\ge\frac{5}{11}\)
Mà : x \(\in Z\) nên : \(x\ge0\) thì : \(B=2x+3.3x-5\ge0\)
Vậy : \(x\ge0\) thỏa mãn đề bài.
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên m để phương trình
9
.
3
2
x
-
m
4
x
2
+
2
x
+
1
4
+
3
m...
Đọc tiếp
Có bao nhiêu số nguyên m để phương trình 9 . 3 2 x - m 4 x 2 + 2 x + 1 4 + 3 m + 3 . 3 x + 1 = 0 có đúng 3 nghiệm phân biệt?
A. Vô số
B. 3
C. 1
D. 2
Tìm
x
∈
N
, biết.a)
3
x
+
1
:
3
4
81
b)
3
x
+
3
.
3
x
+
1
729
c)
2
x...
Đọc tiếp
Tìm x ∈ N , biết.
a) 3 x + 1 : 3 4 = 81
b) 3 x + 3 . 3 x + 1 = 729
c) 2 x + 3 . 2 x = 128
d) 23 + 3 x = 5 6 : 5 3
e) 2 x + 2 x + 4 = 272
Tìm x
∈
N, biết.a,
3
x
+
1
:
3
4
81
b,
3
x
+
3
.
3...
Đọc tiếp
Tìm x ∈ N, biết.
a, 3 x + 1 : 3 4 = 81
b, 3 x + 3 . 3 x + 1 = 729
c, 2 x + 3 . 2 x = 128
d, 23 + 3 x = 5 6 : 5 3
e, 2 x + 2 x + 4 = 272
a, 3 x + 1 : 3 4 = 81
3 x - 3 = 3 4
x – 3 = 4
x = 7
Vậy x = 7
b, 3 x + 3 . 3 x + 1 = 729
3 2 x + 4 = 3 6
2x + 4 = 6
x = 1
Vậy x = 1
c, 2 x + 3 . 2 x = 128
2 2 x + 3 = 2 7
2x + 3 = 7
x = 2
Vậy x = 2
d, 23 + 3 x = 5 6 : 5 3
23 + 3 x = 5 3
23 + 3x = 125
3x = 102
x = 34
Vậy x = 34
e, 2 x + 2 x + 4 = 272
2 x + 2 x . 2 4 = 272
2 x ( 1 + 2 4 ) = 272
2 x . 17 = 272
2 x = 16
2 x = 2 4
x = 4
Vậy x = 4
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của m để phương trình
9
.
3
2
x
-
m
4
x
2
+
2
x
+
1
4
+
3
m...
Đọc tiếp
Có bao nhiêu giá trị nguyên của m để phương trình 9 . 3 2 x - m 4 x 2 + 2 x + 1 4 + 3 m + 3 . 3 x + 1 =0 có đúng 3 nghiệm thực phân biệt
A. Vô số
B. 3
C. 1
D. 2
Ta có
9 . 3 2 x - m ( 4 x 2 + 2 x + 1 4 + 3 m + 3 ) . 3 x + 1 = 0 ⇔ 3 x + 1 + 1 3 x + 1 - m 3 4 x + 1 + 3 m + 3 = 0 1
Đặt t=x+1, phương trình (1) thành
3 t + 1 3 t - m 3 4 x + 1 + 3 m + 3 = 0 2
Bài toán trở thành tìm số giá trị nguyên của m để phương trình (2) có đúng 3 nghiệm thực phân biệt.
Nhận xét: Nếu t 0 là một nghiệm của phương trình (2) thì - t 0 cũng là một nghiệm của phương trình (2). Do đó điều kiện cần để phương trình (2) có đúng 3 nghiệm thực phân biệt là phương trình (2) có nghiệm t=0.
Với t=0 thay vào phương trình (2) ta có
- m 2 - m + 2 = 0 ⇔ [ m = 1 m = - 2
Thử lại:
+) Với m=-2 phương trình (2) thành 3 t + 1 3 t + 2 3 4 t - 3 = 0
Ta có 3 t + 1 3 t ≥ 2 , ∀ t ∈ ℝ và 2 3 4 t - 3 = 0 , ∀ t ∈ ℝ suy ra 3 t + 1 3 t + 2 3 4 t - 3 = 0 ≥ 0 , ∀ t ∈ ℝ
Dấu bằng xảy ra khi t=0, hay phương trình (2) có nghiệm duy nhất t=0 nên loại m=-2
+) Với m=1 phương trình (2) thành 3 t + 1 3 t + 1 3 4 t + 6 = 0 ( 3 )
Dễ thấy phương trình (3) có 3 nghiệm t=-1,t=0,t=1
Ta chứng minh phương trình (3) chỉ có 3 nghiệm t=-1,t=0,t=1.Vì t là nghiệm thì -t cũng là nghiệm phương trình (3) nên ta chỉ xét phương trình (3) trên [ 0 ; + ∞ )
Trên tập [ 0 ; + ∞ ) ,(3) ⇔ 3 t + 1 3 t + 1 3 4 t + 6 = 0
Xét hàm f ' ( x ) = 3 t + 1 3 t + 1 3 4 t + 6 trên [ 0 ; + ∞ )
Ta có
f ' ( t ) = 3 t ln 3 - 3 - t . ln 3 - 2 3 t , f ' ' ( t ) = 3 t ln 2 3 + 3 - t . ln 2 3 + 1 3 . t 3 > 0 , ∀ t > 0
Suy ra f '(t) đồng biến trên ( 0 ; + ∞ ) ⇒ f ' ( t ) = 0 có tối đa 1 nghiệm t > 0 ⇒ f ( t ) = 0 có tối đa 2 nghiệm t ∈ [ 0 ; + ∞ ) . Suy ra trên [ 0 ; + ∞ ) , phương trình (3) có 2 nghiệm t=0, t=1
Do đó trên tập ℝ , phương trình (3) có đúng 3 nghiệm t=-1,t=0,t=1. Vậy chọn m=1
Chú ý: Đối với bài toán trắc nghiệm này, sau khi loại được m=-2 ta có thể kết luận đáp án C do đề không có phương án nào là không tồn tại m.
Chọn đáp án C.
Đúng 0
Bình luận (0)
Giải các bất phương trình sau:
4
x
2
+
3
.
3
x
+
x
.
3
x
2
x
2
.
3
x...
Đọc tiếp
Giải các bất phương trình sau: 4 x 2 + 3 . 3 x + x . 3 x < 2 x 2 . 3 x + 2 x + 6
Ta có bất phương trình đã cho tương đương với
4 x 2 + 3 . 3 x + x . 3 x - 2 x 2 . 3 x - 2 x - 6 < 0
⇔ 3 + x - 2 x 2 3 x − 2(x − 2 x 2 + 3) < 0
⇔(−2 x 2 + x + 3)( 3 x − 2) < 0
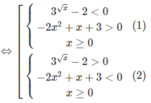
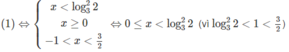
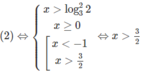
Vậy nghiệm của bất phương trình là x > 3/2 hoặc
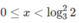
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của m để phương trình
9
.
x
2
x
-
m
4
x
2
+
2
x
+
1
4
+
3
m...
Đọc tiếp
Có bao nhiêu giá trị nguyên của m để phương trình 9 . x 2 x - m 4 x 2 + 2 x + 1 4 + 3 m + 3 . 3 x + 1 = 0 có đúng 3 nghiệm thực phân biệt
A. Vô số
B. 3
C. 1
D. 2