Cho 4 điểm A,B,C,D bất kì .Hãy xác định số đường thẳng vẽ đc từ 4 điểm trên

Những câu hỏi liên quan
Cho 4 điểm A,B,C,D bất kì. Hãy xác định số đường thẳng vẽ được từ 4 điểm đó
cho 4 điểm a,b,c,d trong đó ko có 3 điểm nào thẳng hàng qua hai điểm bất kì vẽ đc 1 đường thẳng hỏi có bao nhiêu đg thẳng đc tạo thành? số đg thẳng này thay đổi ntn nếu trg 4 điểm đó có 3 điểm thẳng hàng
a) vẽ theo diễn đạt sau
+vẽ dường thẳng bất kì
+trên đường thẳng xác định điểm A,B,C,D
+lấy e ko thuộc đường thẳng
b)kể tên +các bộ ba điểm thẳng hàng
+các bộ ba điểm ko thẳng hàng
+các đường thẳng đi qua 2 trong 4 điểm A,B,C,D
a) ________________________
b)_____A____________B___________________C___________________D__________________
c)_____A____________B___________________C___________________D__________________ .E
d)ABC ; BCD; ACD ;
dường thẳng AB ( AC;AD;BC;BD;CD)
Đúng 0
Bình luận (0)
Cho A là một điểm bất kì nằm ngoài đường thẳng d. Xác định khoảng cách từ A đến đường thẳng d
Chỉ cần vẽ đường cao kẻ từ A xuống d
Đúng 0
Bình luận (0)
Cho (O;R) vẽ 1 đường thẳng d ko cắt (O) trên đường thẳng d lấy một điểm A bất kì từ A kẻ các tiếp tuyến AB AC với đường tròn (B,C là các tiếp điểm)
CM A,B,O,C thẳng hàng
Gọi I là trung điểm của OA.
Có AB,AC là tiếp tuyến của (O;R)
=> OB⊥AB; OC⊥CA
Xét △ABO vuông tại B có BI là đường trung tuyến
=> BI = IO =IA (1)
Xét △ACO vuông tại C có CI là đường trung tuyến
=> CI =IO =IA (2)
Từ (1) và (2) => IB = IC=IA = IO
=> A,B,O,C cùng nằm trên một đường tròn.
Đúng 0
Bình luận (0)
Cho trước một số điểm trong đó không có ba điểm bất kì nào thẳng hàng. Hỏi vẽ được bao nhiêu đường thẳng nếu số điểm cho trước là: a) 4 điểm A, B, C, D;b) 5 điểmA, B, C, D, E;c) n điểm
n
∈
N
;
n
≥
2
?
Đọc tiếp
Cho trước một số điểm trong đó không có ba điểm bất kì nào thẳng hàng. Hỏi vẽ được bao nhiêu đường thẳng nếu số điểm cho trước là:
a) 4 điểm A, B, C, D;
b) 5 điểmA, B, C, D, E;
c) n điểm n ∈ N ; n ≥ 2 ?
a) Với 4 điểm A, B, C, D cho trước trong đó không có ba điểm bất kì nào thẳng hàng thì có thể vẽ được 6 đường thẳng là: AB , AC , AD , BC , BD , CD .
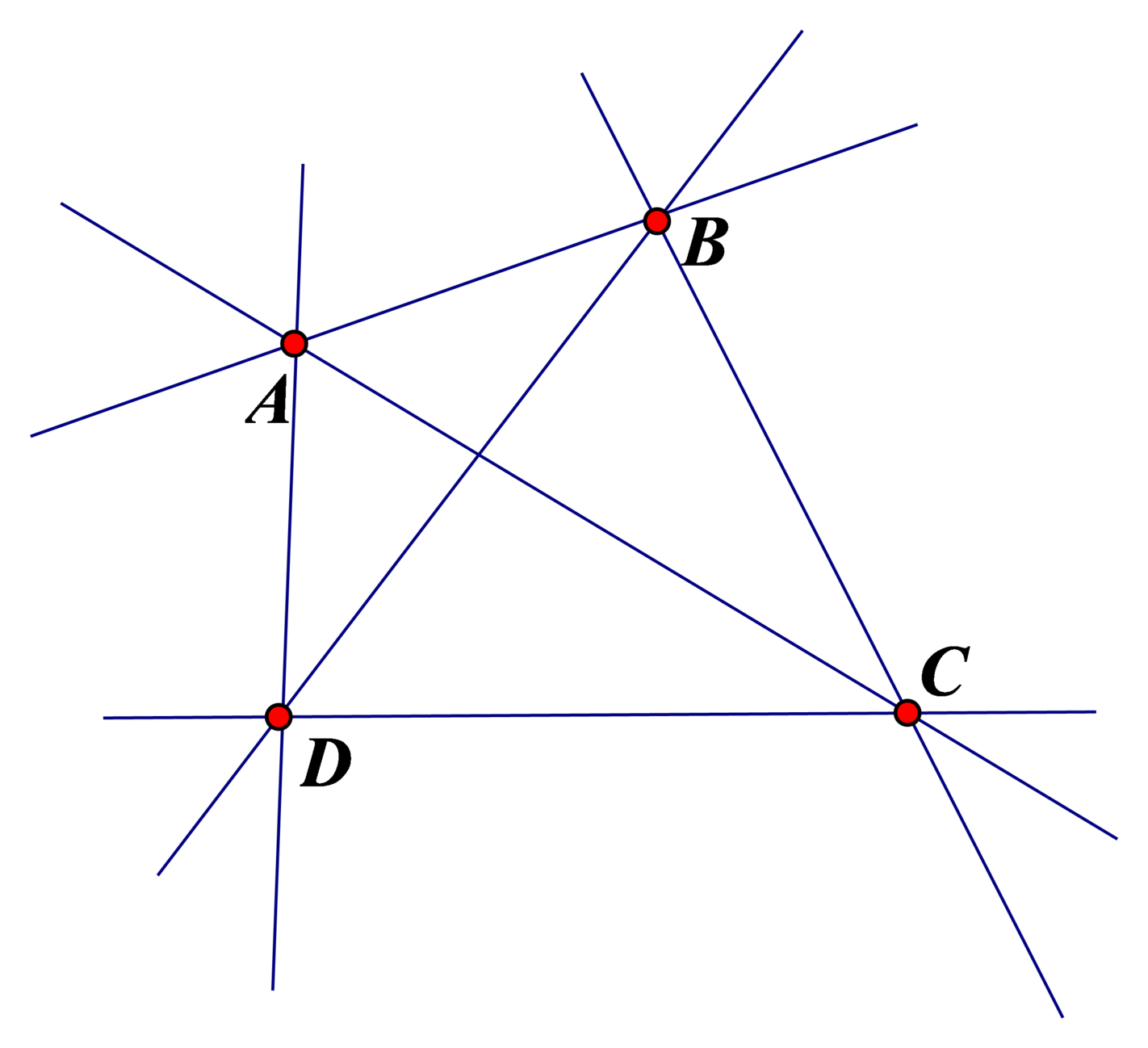
b) Với 5 điểm A, B, C, D, E cho trước trong đó không có ba điểm bất kì nào thẳng hàng thì có thể vẽ được 10 đường thẳng là: AB , AC , AD , AE , BC , BD , BE , CD , CE , DE .
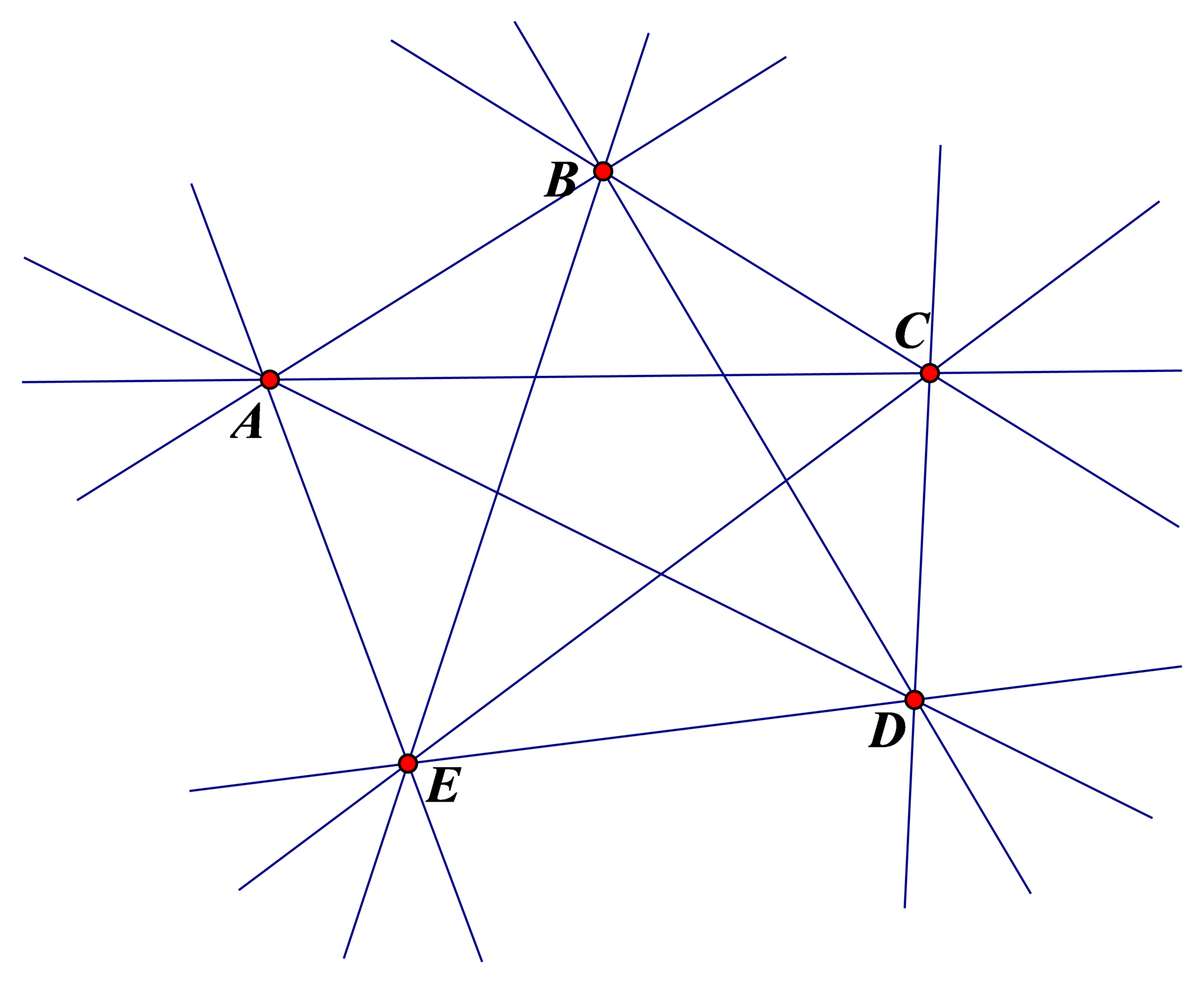
c) Chọn một trong số n điểm đã cho rồi nối điểm đó với n-1 điểm còn lại ta được n-1 đường thẳng.
Làm như vậy với tất cả n điểm ta được n(n-1) đường thẳng. Nhưng mỗi đường thẳng được tính hai lần, do đó ta vẽ được n . n − 1 2 đường thẳng.
Đúng 0
Bình luận (0)
cho hàm số y = ( 2m - 1 ) *
a) tìm m biết điểm A ( 2 ; 4 ) thuộc đồ thị hàm số trên. viết công thức xác định hàm số trên
b) Hãy vẽ đồ thị hàm số trên
c) Đánh dấu ác điểm B(-2;-4), C(-3;0),D(0;2), E(-1/2;-1) trên cùng mặt phẳng tọa độ Õy
d) Hãy chỉ ra các điểm nào cùng thuộc đường thẳng OA
Cho đường thẳng xy. Từ một điểm O trên đường thẳng xy, ta vẽ hai tia Oz và Ot như Hình 2.
a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB.
b) Đoạn thẳng AB có cắt đường thẳng xy hay không?

a)

b) Đoạn thẳng AB cắt đường thẳng xy
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R và đường thẳng d cố định không cắt đường tròn . Từ điểm A bất kì trên đường thẳng d kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm) . Từ B kẻ đường thẳng vuông góc với OH tại H , trên tia đối của tia HB lấy điểm C sao cho HCHB.A,Chứng minh điểm C thuộc (O;R) và AC là tiếp tuyến của đường tròn (O)B,Từ O kẻ đường thẳng vuông góc với đường thẳng d tại I , OI cắt BC tại IC. Chứng minh OH.OAOI.OKR^2
Đọc tiếp
Cho đường tròn tâm O bán kính R và đường thẳng d cố định không cắt đường tròn . Từ điểm A bất kì trên đường thẳng d kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm) . Từ B kẻ đường thẳng vuông góc với OH tại H , trên tia đối của tia HB lấy điểm C sao cho HC=HB.
A,Chứng minh điểm C thuộc (O;R) và AC là tiếp tuyến của đường tròn (O)
B,Từ O kẻ đường thẳng vuông góc với đường thẳng d tại I , OI cắt BC tại IC. Chứng minh OH.OA=OI.OK=R^2

















