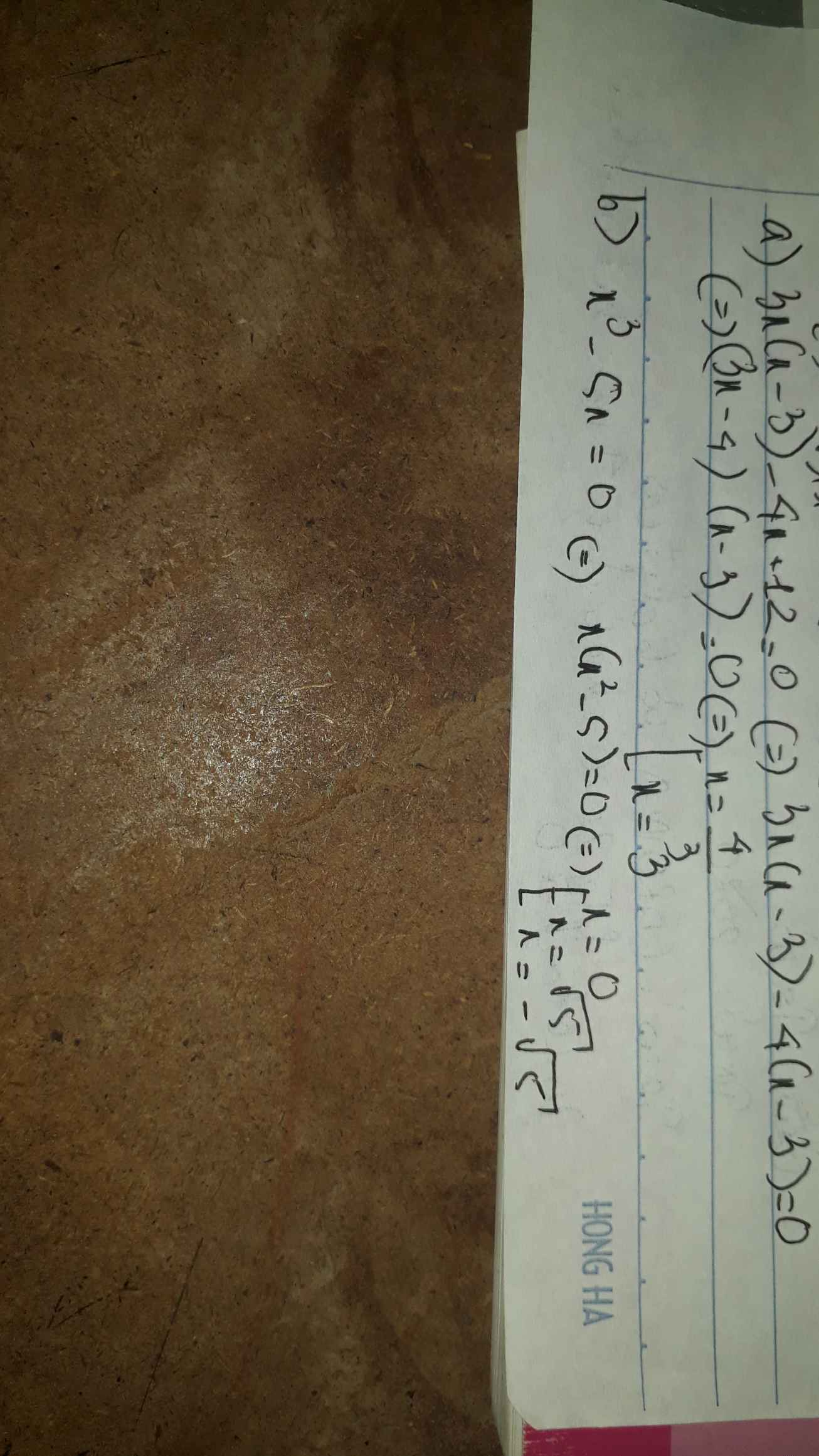a) Ta có: \(x^2-2x+1=0\)

\(\Leftrightarrow\left(x-1\right)^2=0\)

\(\Leftrightarrow x-1=0\)hay x=1

Vậy: S={1}

c) Ta có: \(x+x^4=0\)

\(\Leftrightarrow x\left(x^3+1\right)=0\)

\(\Leftrightarrow x\left(x+1\right)\left(x^2-x+1\right)=0\)

mà \(x^2-x+1>0\forall x\)

nên x(x+1)=0

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)

Vậy: S={0;-1}

a: \(x^3-4x^2-x+4=0\)

=>\(\left(x^3-4x^2\right)-\left(x-4\right)=0\)

=>\(x^2\left(x-4\right)-\left(x-4\right)=0\)

=>\(\left(x-4\right)\left(x^2-1\right)=0\)

=>\(\left[{}\begin{matrix}x-4=0\\x^2-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x^2=1\end{matrix}\right.\Leftrightarrow x\in\left\{2;1;-1\right\}\)

b: Sửa đề: \(x^3+3x^2+3x+1=0\)

=>\(x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3=0\)

=>\(\left(x+1\right)^3=0\)

=>x+1=0

=>x=-1

c: \(x^3+3x^2-4x-12=0\)

=>\(\left(x^3+3x^2\right)-\left(4x+12\right)=0\)

=>\(x^2\cdot\left(x+3\right)-4\left(x+3\right)=0\)

=>\(\left(x+3\right)\left(x^2-4\right)=0\)

=>\(\left(x+3\right)\left(x-2\right)\left(x+2\right)=0\)

=>\(\left[{}\begin{matrix}x+3=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\\x=-2\end{matrix}\right.\)

d: \(\left(x-2\right)^2-4x+8=0\)

=>\(\left(x-2\right)^2-\left(4x-8\right)=0\)

=>\(\left(x-2\right)^2-4\left(x-2\right)=0\)

=>\(\left(x-2\right)\left(x-2-4\right)=0\)

=>(x-2)(x-6)=0

=>\(\left[{}\begin{matrix}x-2=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=6\end{matrix}\right.\)

b: \(3x^2-2x-1=0\)

=>\(3x^2-3x+x-1=0\)

=>\(\left(x-1\right)\left(3x+1\right)=0\)

=>\(\left[{}\begin{matrix}x-1=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)

a: Bạn ghi lại đề đi bạn

\(a,x^3+3x^2=4x+12\)

\(x^2\left(x+3\right)=4\left(x+3\right)\)

\(\Rightarrow\left(x+3\right)\left(x^2-4\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x+3=0\\x^2-4=0\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=-3\\x=\pm2\end{cases}}\)

\(b,49x^2=\left(3x+2\right)^2\)

\(7x=3x+2\)

\(\Rightarrow7x-3x=2\)

\(\Rightarrow4x=2\)

\(\Rightarrow x=\frac{1}{2}\)

các câu còn lại tương tự nha

\(a,x^3+3x^2=4x+12\)

\(x^3+3x^2-4x-12=0\)

\(\Rightarrow x^2\left(x+3\right)-4\left(x+3\right)=0\)

\(\Rightarrow\left(x+3\right)\left(x^2-4\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x+3=0\\\left(x+2\right)\left(x-2\right)=0\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=-3\\x=\pm2\end{cases}}\)

\(b,49x^2=\left(3x+2\right)^2\)

\(\Rightarrow\left(7x\right)^2=\left(3x+2\right)^2\)

\(\Rightarrow7x=3x+2\)

\(\Rightarrow7x-3x=2\)

\(\Rightarrow4x=2\)

\(\Rightarrow x=\frac{1}{2}\)

\(c,3x^2\left(x-5\right)+12\left(5-x\right)=0\)

\(3x^2\left(x-5\right)-12\left(x-5\right)=0\)

\(\left(x-5\right)\left(3x^2-12\right)=0\)

\(\Rightarrow3.\left(x-5\right)\left(x^2-4\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x-5=0\\x^2-4=0\end{cases}\Rightarrow\orbr{\begin{cases}x=5\\x=\pm2\end{cases}}}\)

\(d,x^2\left(x-5\right)+45-9x=0\)

\(x^2\left(x-5\right)+9\left(5-x\right)=0\)

\(x^2\left(x-5\right)-9\left(x-5\right)=0\)

\(\left(x-5\right)\left(x^2-9\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x-5=0\\x^2-9=0\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=5\\x=\pm3\end{cases}}\)

a, <=> (x-1)^3 + x^2(x-1)=0

<=> (x-1)(x^2-2x+1+x^2)=0

<=> (x-1)(2x^2-2x+1)=0

=> x=1

2x^2-2x+1=0 (*)

giải (*):

2x^2-2x+1=0

<=> (x-1)^2 + x^2 > 0

=> * vô nghiệm

=> Pt có nghiệm là 1.

b, x^2+x-12=0

<=> (x-3)(x+4)=0

=> x=3 hoặc x = -4

vậy....

c, 6x^2-11x-10=0

<=> (x-5/2)(6x+4)=0

=> x=5/2 hoặc x= -2/3.

vậy...

giúp mình với ;-;

ghi này chả hiểu j bn ak

ghi rõ ra coi

tui chịu,???

a) \(2x^3+3x^2-8x-12=0\)

\(\Leftrightarrow\left(2x^3-8x\right)+\left(3x^2-12\right)=0\)

\(\Leftrightarrow2x\left(x^2-4\right)+3\left(x^2-4\right)=0\)

\(\Leftrightarrow\left(x^2-4\right)\left(2x+3\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(2x+3\right)=0\)

\(\Leftrightarrow\)\(x-2=0\)

hoặc \(x+2=0\)

hoặc \(2x+3=0\)

\(\Leftrightarrow\)\(x=2\)

hoặc \(x=-2\)

hoặc \(x=-\frac{3}{2}\)

Vậy tập nghiệm của phương trình là \(S=\left\{2;-2;-\frac{3}{2}\right\}\)

b) \(x^3-4x^2-x+4=0\)

\(\Leftrightarrow x^2\left(x-4\right)-\left(x-4\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x^2-1\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x-1\right)\left(x+1\right)=0\)

\(\Leftrightarrow\)\(x-4=0\)

hoặc \(x-1=0\)

hoặc \(x+1=0\)

\(\Leftrightarrow\)\(x=4\)

hoặc \(x=1\)

hoặc \(x=-1\)

Vậy tập nghiệm của phương trình là \(S=\left\{4;1;-1\right\}\)

c) \(x^3-x^2-x-2=0\)

\(\Leftrightarrow x^3-2x^2+x^2-2x+x-2=0\)

\(\Leftrightarrow x^2\left(x-2\right)+x\left(x-2\right)+\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^2+x+1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x^2+x+1=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=2\left(tm\right)\\\left(x+\frac{1}{2}\right)^2+\frac{3}{4}=0\left(ktm\right)\end{cases}}\)

Vậy tập nghiệm của phương trình là \(S=\left\{2\right\}\)

d) \(x^4-3x^3+3x^2-x=0\)

\(\Leftrightarrow x\left(x^3-3x^2+3x-1\right)=0\)

\(\Leftrightarrow x\left(x-1\right)^3=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-1=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=1\end{cases}}\)

Vậy tập nghiệm của phương trình là \(S=\left\{0;1\right\}\)

e) \(\left(x+1\right)\left(x^2-2x+3\right)=x^3+1\)

\(\Leftrightarrow\left(x+1\right)\left(x^2-2x+3\right)=\left(x+1\right)\left(x^2-x+1\right)\)

\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x^2-2x+3=x^2-x+1\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=-1\\x=2\end{cases}}\)

Vậy tập nghiệm của phương trình là \(S=\left\{-1;2\right\}\)

g) \(x^3+3x^2+3x+1=4x+4\)

\(\Leftrightarrow\left(x+1\right)^3=4\left(x+1\right)\)

\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\\left(x+1\right)^2=4\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=-1\\x+1=\pm2\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=-1\\x=-3\end{cases}}\)  hoặc   \(x=1\)

Vậy tập nghiệm của phương trình là \(S=\left\{-1;1;-3\right\}\)

b) \(x^3-4x^2-x+4=0\)

\(\Leftrightarrow x^2\left(x-4\right)-\left(x-4\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x^2-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-4=0\\x^2-1=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=\pm1\end{cases}}\)

c) \(x^3-x^2-x-2=0\)

\(\Leftrightarrow x^3-2x^2+x^2-2x+x-2=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^2+x+1\right)=0\)

\(\Leftrightarrow x=2\) ( Do \(x^2+x+1>0\) )

a) \(2x^3+3x^2-8x-12=0\)

\(\Leftrightarrow x^2\left(2x+3\right)-4\left(2x+3\right)=0\)

\(\Leftrightarrow\left(2x+3\right)\left(x^2-4\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}2x+3=0\\x^2-4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{3}{2}\\x=\pm2\end{cases}}\)

\(a,=3x-9-4x+12=-x+3=0\)

\(\Leftrightarrow x=3\)

Vậy ..

\(b,=\left(x+2\right)\left(x+2-x+2\right)=4\left(x+2\right)=0\)

\(\Leftrightarrow x+2=0\)

\(\Leftrightarrow x=-2\)

Vậy ..

\(c,=x^3-3x^2+3x-1=\left(x-1\right)^3=0\)

\(\Leftrightarrow x=1\)

Vậy ..

\(d,\Leftrightarrow x\left(x-2\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)

Vậy ..

\(e,=\left(2x-3-5\right)\left(2x-3+5\right)=\left(2x-8\right)\left(2x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{8}{2}=4\\x=-\dfrac{2}{2}=-1\end{matrix}\right.\)

Vậy ...

a) Ta có: 3(x-3)-4x+12=0

\(\Leftrightarrow3\left(x-3\right)-4\left(x-3\right)=0\)

\(\Leftrightarrow x-3=0\)

hay x=3

Vậy: S={3}

b) Ta có: \(\left(x+2\right)^2-\left(x+2\right)\left(x-2\right)=0\)

\(\Leftrightarrow x^2+4x+4-x^2+4=0\)

\(\Leftrightarrow4x=-8\)

hay x=-2

Vậy: S={-2}

c) Ta có: \(x^3+3x=3x^2+1\)

\(\Leftrightarrow x^3-3x^2+3x-1=0\)

\(\Leftrightarrow x-1=0\)

hay x=1

Vậy: S={1}

d) Ta có: \(\dfrac{2}{3}x\left(x^2-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)

Vậy: S={0;2;-2}

a) 3.(x-3)-4x+12=0

=> 3x - 9 - 4x + 12 = 0

=> -x + 3 = 0

=> x = 3

b) (x+2)^2-(x+2).(x-2) =0

\(\Rightarrow\left(x+2\right)^2-x^2+4=0\)

\(\Rightarrow x^2+4x+4-x^2+4=0\)

=> 4x + 8 = 0

=> x = -2

c) x^3+3x=3x^2+1

\(\Rightarrow x^3+3x-3x^2-1=0\)

\(\Rightarrow\left(x-1\right)^3=0\)

=> x = 1

d) \(\dfrac{2}{3}x\left(x^2-4\right)=0\)

\(\Rightarrow\dfrac{2}{3}x\left(x-2\right)\left(x+2\right)=0\)

=> x = 0 hoặc x = 2 hoặc x = -2

e) \(\left(2x-3\right)^2-5^2=0\)

\(\Rightarrow\left(2x-8\right)\left(2x+2\right)=0\)

=> x = 4 hoăc x = -1