ddddddddddddddddddddd

sorry thằng em nó lam nhé 

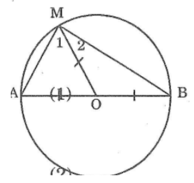
Nối OM, ta có:

OA = OM (bán kính đường tròn tâm O)

Nên ΔOAM cân tại O

⇒∠A =∠M1(tính chất tam giác cân)(1)

OM = OB (bán kính đường tròn tâm O)

Suy ra: ΔOBM cân tại O

⇒∠B =∠M2(tính chất tam giác cân) (2)

Trong ΔAMB ta có:

∠A + ∠AMB + ∠B = 180º (tổng ba góc trong tam giác)

⇒∠A +∠B +∠M1+∠M2 =180 (3)

Từ (1), (2) và (3) suy ra: 2(∠M1 + ∠M2)=180o

Vậy: ∠M1+∠M2=90o hay ∠(AMB) =90o

(h.141)\(\Delta AOM\) cân \(\Rightarrow\)\(\widehat{A}=\widehat{M1}\)

\(\Delta BOM\) cân \(\Rightarrow\)\(\widehat{B}=\widehat{M2}\)

Suy ra \(\widehat{M1}+\widehat{M2}=\widehat{A}+\widehat{B}\)do đó

\(\widehat{AMB}=\widehat{A}+\widehat{B}\).Ta lại có:

\(\widehat{AMB}+\widehat{A}+\widehat{B}=180^0\) nên

\(\widehat{AMB}=90^0\)

(h.141)

cân

Suy ra do đó

.Ta lại có:

nên

vì M thuộc đường tròn tâm C đường kính AB nen ta có CA=CM=CB=R

vậy tam giác CAM cân tại C và tam giác CBM cân tại C

vì tam giác CAM cân tại C nên ta có góc CMA = góc CAM = (180-góc ACM):2

vì tam giác CBM cân tại C nên ta có góc CBM= góc CMB= (180-góc BCM):2

ta lại có góc AMB= góc AMC + góc BMC=\(\frac{180-gócACM}{2}\frac{ }{ }\)+\(\frac{180-gócBCM}{2}\frac{ }{ }\)=\(\frac{180+180-gócACM-gócBCM}{2}\frac{ }{ }\)=\(\frac{360-gócACB}{2}\frac{ }{ }\)=\(\frac{360-180}{2}\frac{ }{ }\)=90 độ

Giải thích các bước giải:

MO là t.p.g. của AMBˆAMB^

⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450

⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân

=> OA = AM = MB = BO

=> OAMB là h.thoi có AMBˆ=900AMB^=900

=> OAMB là h.v.

b)

PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ

=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)

=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)

=MA+MB=MA+MB

=2OA=2OA

=2R=2R

c)

OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^

⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)

OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^

⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)

Cộng theo vế của (1) và (2), ta có:

COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^

⇒POQˆ=450

Giải thích các bước giải:

MO là t.p.g. của AMBˆAMB^

⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450

⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân

=> OA = AM = MB = BO

=> OAMB là h.thoi có AMBˆ=900AMB^=900

=> OAMB là h.v.

b)

PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ

=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)

=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)

=MA+MB=MA+MB

=2OA=2OA

=2R=2R

c)

OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^

⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)

OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^

⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)

Cộng theo vế của (1) và (2), ta có:

COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^

⇒POQˆ=450vv

Bài 7:

a: Xét ΔOAM vuông tại A có 

\(\cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{1}{2}\)

nên \(\widehat{AOM}=60^0\)

b: Xét tứ giác OAMB có 

\(\widehat{OAM}+\widehat{OBM}=180^0\)

Do đó: OAMB là tứ giác nội tiếp

Suy ra: \(\widehat{AOB}=180^0-36^0=144^0\)

a: Đề bài này chưa đủ dữ kiện để tính góc OAC nha bạn 

ΔOAC cân tại O

mà OD là đường trung tuyến

nên OD\(\perp\)AC và OD là phân giác của góc AOC

Xét (O) có

ΔACB nội tiếp

AB là đường kính

Do đó: ΔACB vuông tại C

=>AC\(\perp\)CB

mà OD\(\perp\)AC

nên OD//CB

b: Xét ΔOAE và ΔOCE có

OA=OC

\(\widehat{AOE}=\widehat{COE}\)

OE chung

Do đó: ΔOAE=ΔOCE

=>\(\widehat{OAE}=\widehat{OCE}=90^0\)

=>EC là tiếp tuyến của (O)