Bài 1

Quy ước: A: cao;                 a: thấp

Các kiểu gen cây thân cao : AA; Aa

                       Cây thân thấp aa

Bài2 

Vì F1 thu dc toàn quả tròn => tính trạng tròn trội hoàn toàn so với tính trạng quả bầu dục

Quy ước gen A: quả tròn.           a: quả bầu dục

P(t/c).   AA( tròn).         x.           aa( bầu dục)

Gp.       A.                                   a

F1.        Aa( quả tròn)

F1xF1.   Aa( tròn).        X.            Aa( tròn)

GF1         A,a.                           A,a

F2.       1 AA:2Aa:1aa

   Kiểu hình: 3 tròn:1 bầu dục

mình ko biết mới học lớp 4 à . mà đề lớp mấy vậy bạn ????

Bài 1

Quy ước: A: cao; a: thấp

Các kiểu gen cây thân cao : AA; Aa

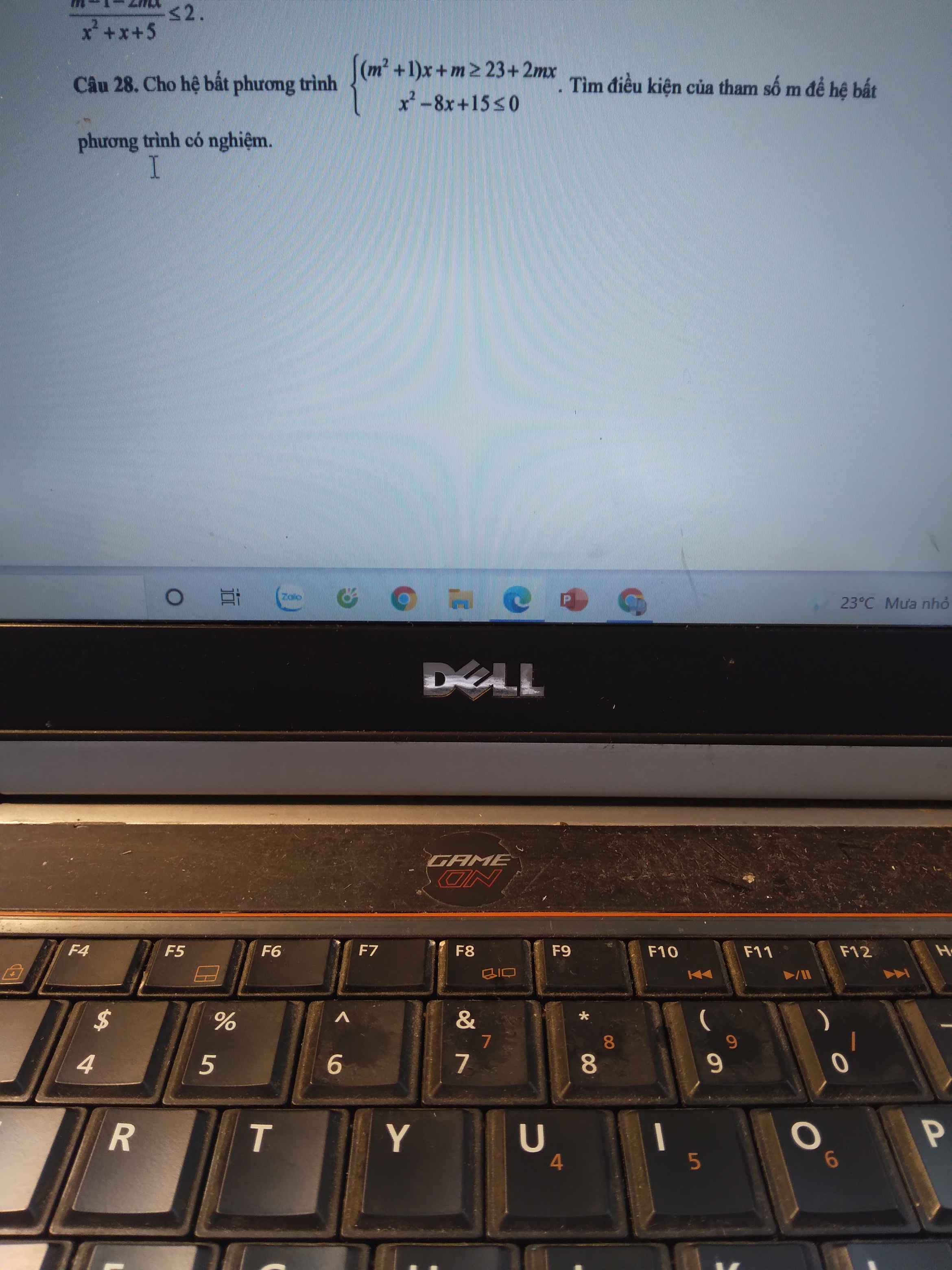
Xét BPT: \(x^2-8x+15\le0\Leftrightarrow3\le x\le5\Rightarrow D_1=\left[3;5\right]\)

Xét BPT: \(\left(m^2+1\right)x+m\ge23+2mx\)

\(\Leftrightarrow\left(m^2-2m+1\right)x\ge23-m\)

\(\Leftrightarrow\left(m-1\right)^2x\ge23-m\) (1)

- Với \(m=1\Rightarrow\left(1\right)\) trở thành \(0\ge22\) (vô lý) \(\Rightarrow\left(1\right)\) vô nghiệm (loại)

- Với \(m\ne1\Rightarrow\left(m-1\right)^2>0;\forall m\)

\(\left(1\right)\Leftrightarrow x\ge\dfrac{23-m}{\left(m-1\right)^2}\) \(\Rightarrow D_2=\left[\dfrac{23-m}{(m-1)^2};+\infty \right)\)

Hệ đã cho có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)

\(\Rightarrow\dfrac{23-m}{\left(m-1\right)^2}\le5\)

\(\Leftrightarrow23-m\le5\left(m-1\right)^2\)

\(\Leftrightarrow5m^2-9m-18\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-\dfrac{6}{5}\end{matrix}\right.\)

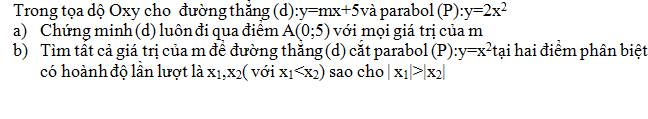
a: Thay x=0 và y=5 vào (d), ta được:

m*0+5=5

=>5=5(đúng)

=>ĐPCM

b: x1<x2; |x1|>|x2|

=>x1*x2<0

PTHĐGĐ là:

x^2-mx-5=0

Vì a*c<0

nên x1,x2 luôn trái dấu

=>Với mọi m

Câu 1:

\(\left(4x+3\right)\left(3x^2+x-2\right)\left(2x^2-3x-5\right)=0\\ \Leftrightarrow\left(4x+3\right)\left(3x-2\right)\left(x+1\right)\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=-1\\x=\dfrac{2}{3}\\x=\dfrac{5}{2}\end{matrix}\right.\\ \Leftrightarrow A=\left\{-1;-\dfrac{3}{4};\dfrac{2}{3};\dfrac{5}{2}\right\}\)

Câu 2:

\(\left(x^2-4\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=3\end{matrix}\right.\Leftrightarrow A=\left\{-2;2;3\right\}\\ \left|5x\right|-11\le0\Leftrightarrow\left|5x\right|\le11\Leftrightarrow-11\le5x\le11\\ \Leftrightarrow-\dfrac{11}{5}\le x\le\dfrac{11}{5}\\ \Leftrightarrow B=\left[-\dfrac{11}{5};\dfrac{11}{5}\right]\)

\(\Leftrightarrow A\cap B=\left\{-2;2\right\}\\ A\cup B=\left[-\dfrac{11}{5};3\right]\\ A\B=\left\{3\right\}\)

26: A

27: D

28:A

29:A

30:A

31:C

32:B

33:A

1.

a.

\(n^2+7n+1=k^2\Rightarrow4n^2+28n+4=4k^2\)

\(\Leftrightarrow\left(2n+7\right)^2-45=\left(2k\right)^2\)

\(\Leftrightarrow\left(2n-2k+7\right)\left(2n+2k+7\right)=45\)

Phương trình ước số cơ bản

b.

\(a^3b^3+b^3-3ab^2=-1\)

\(\Leftrightarrow a^3+1-\dfrac{3a}{b}=-\dfrac{1}{b^3}\)

\(\Leftrightarrow a^3+\dfrac{1}{b^3}+1-\dfrac{3a}{b}=0\)

Đặt \(\left(a;\dfrac{1}{b}\right)=\left(x;y\right)\Rightarrow x^3+y^3+1-3xy=0\)

\(\Leftrightarrow\left(x+y\right)^3+1-3xy\left(x+y\right)-3xy=0\)

\(\Leftrightarrow\left(x+y+1\right)\left(x^2+y^2+1-xy-x-y\right)=0\)

\(\Leftrightarrow x+y+1=0\)

\(\Rightarrow P=a+\dfrac{1}{b}=x+y=-1\)

2.

a.

 \(a+b+\dfrac{1}{a}+\dfrac{1}{b}=\left(\dfrac{a}{4}+\dfrac{1}{a}\right)+\left(\dfrac{b}{4}+\dfrac{1}{b}\right)+\dfrac{3}{4}\left(a+b\right)\)

\(\ge2\sqrt{\dfrac{a}{4a}}+2\sqrt{\dfrac{b}{4b}}+\dfrac{3}{4}.4=5\) (đpcm)

Dấu "=" xảy ra khi \(a=b=2\)

2.b

b.

\(\Leftrightarrow x^4+4x+4=y^4+4y+4\)

\(\Leftrightarrow\left(x+2\right)^2=y^4+4y+4\)

\(\Rightarrow y^4+4y+4\) là số chính phương

Ta có: \(y^4+4y+4>y^4\) với mọi y nguyên dương

\(y^4+4y+4\le y^4+4y^2+4=\left(y^2+2\right)^2\)

\(\Rightarrow\left(y^2\right)^2< y^4+4y+4\le\left(y^2+2\right)^2\)

\(\Rightarrow\left[{}\begin{matrix}y^4+4y+4=\left(y^2+1\right)^2\\y^4+4y+4=\left(y^2+2\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2y^2-4y-3=0\left(ktm\right)\\y^2-y=0\Rightarrow y=1\end{matrix}\right.\)

Thế vào pt ban đầu \(\Rightarrow x^2+4x=5\Rightarrow x=1\)

Vậy \(\left(x;y\right)=\left(1;1\right)\)