Hàm số bậc nhất y= căn(2*x) có hệ số a=?

Những câu hỏi liên quan
xác định hàm số bậc nhất y \(=\) ax + b, biết đồ thị hàm số có hệ số góc là -2 và cắt trục hoành tại điểm có hoành độ là 2
Hệ số góc là `-2` `=> a=-2`
Với `a=-2` ta có hàm số `y=-2x+b`
Đồ thị h/s cắt trục hoành tại điểm có hoành độ là `2` nên `y=-2x+b` đi qua điểm `(2;0)`
`0=-2*2+b`
`<=> 0 = -4+b`
`<=>b=4`
Vậy hàm số bậc nhất là : `y=-2x+4`
Đúng 3
Bình luận (0)
Hàm số bậc hai
y
f
x
a
2
+
b
x
+
c
a
≠
0
nhận giá trị bằng 1 khi x1 và đạt giá trị nhỏ nhất bằng
3
4
khi
x
1
2
thì có tích các hệ số là A. abc-1 B. abc1 C. abc-3...
Đọc tiếp
Hàm số bậc hai y = f x = a 2 + b x + c a ≠ 0 nhận giá trị bằng 1 khi x=1 và đạt giá trị nhỏ nhất bằng 3 4 khi x = 1 2 thì có tích các hệ số là
A. abc=-1
B. abc=1
C. abc=-3
D. abc=3
Cho hàm số bậc nhất y =- kx +k:^2+3 tìm k để đồ thị hàm số đồng biến trên R
Xem chi tiết
bn có thể viết rõ hơn được ko?
-kx + k^2 + 3 hay là gì?
Đúng 0
Bình luận (0)
Đề là hàm số \(y=-kx+k^2+3\) phải kh.
Đồ thị hàm số đã cho đồng biến trên R khi \(-k>0\Leftrightarrow k< 0\)
Đúng 1
Bình luận (0)
Cho hàm số bậc ba yf(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y|f(x)+m| có ba điểm cực trị là: A.
m
≤
-
1
hoặc
m
≥
3
B.
m
≤
-
3
hoặc
m
≥
1
C. m -1 hoặc m 3 D.
1
≤
m
≤
3
Đọc tiếp
Cho hàm số bậc ba y=f(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y=|f(x)+m| có ba điểm cực trị là:
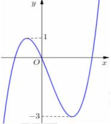
A. m ≤ - 1 hoặc m ≥ 3
B. m ≤ - 3 hoặc m ≥ 1
C. m = -1 hoặc m = 3
D. 1 ≤ m ≤ 3
tìm m để các hàm số sau là hàm bậc nhất:
a) y=(2m-1)x^2 + (m+1)x-3
b) (m^2+3m+7)x-2
Cho C=x^4-x^3+2x^2-11x-5 phân tích đa thức thành 2 tam thức bậc 2 với hệ số nguyên và các hệ số bậc cao nhất đều dấu dương
Ai giải đc giúp mk cái
Đa thức P(x) bậc 4 có hệ số bậc cao nhất là 1. Biết P(1)=0; P(3)=0; P(5)=0
Tính giá trị của biểu thức: Q= P(-2) + 7P(6)
. Ta có: P(1)= 0, P(3)= 0, P(5)= 0 => 1,3,5 là nghiệm của pt, nên P(x) chứa nhân tử: (x-1) ; (x-3) ; (x-5)
. Vì P(x) bậc 4, có hệ số bậc cao nhất là 1 nên P(x) có dạng: \(\left(x-1\right)\left(x-3\right)\left(x-5\right)\left(x-a\right)\)
. \(Q=P\left(-2\right)+7P\left(-6\right)\) = \(\left(-2-1\right)\left(-2-3\right)\left(-2-5\right)\left(-2-a\right)+7\left(6-1\right)\left(6-3\right)\left(6-5\right)\left(6-a\right)\)
\(=210+105a+630-105a\) \(=840\)
. Vậy \(Q=840\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng nếu các hệ số của pt bậc 2
x2+p1x +q1=0 và x2+p2x+q2=0
Liên hệ với nhau bởi hệ thức p1p2 >=2(q1+q2) thì ít nhất 1 trong 2 pt có nghiệm?
GIÚP MÌNH VỚI!
Giả sử 2 pt vô nghiệm. Khi đó \(p_1^2< 4q_1;p_2^2< 4q_2\Rightarrow p_1^2+p_2^2< 4\left(q_1+q_2\right)\le2p_1p_2\Leftrightarrow\left(p_1-p_2\right)^2< 0\). (vô lí)
Do đó tồn tại 1 pt có nghiệm
Đúng 1
Bình luận (0)
Cho đa thức bậc 4 : P(x) có hệ số cao nhất là 1. BIết P(1) = 0 ; P(3) = 0 ; P(5) = 0. Tính M = P(-2) + 7. P(6) + 201