Cho (0:5cm)dây AB=9,6cm Tính khoảng cách từ O đến AB

Những câu hỏi liên quan
Cho (O ; 5cm) , dây AB = 9,6cm . Tính khoảng cách từ O đến AB.
Gọi OK là khoảng cách từ O đến dây AB
Suy ra: OK\(\perp\)AB tại K và K là trung điểm của AB
Vì K là trung điểm của AB
nên \(AK=BK=\dfrac{9.6}{2}=4.8cm\)
Áp dụng định lí Pytago vào ΔOAK vuông tại K, ta được:
\(OA^2=AK^2+KO^2\)
\(\Leftrightarrow OK^2=1.96\)
hay OK=1,4cm
Đúng 1
Bình luận (0)
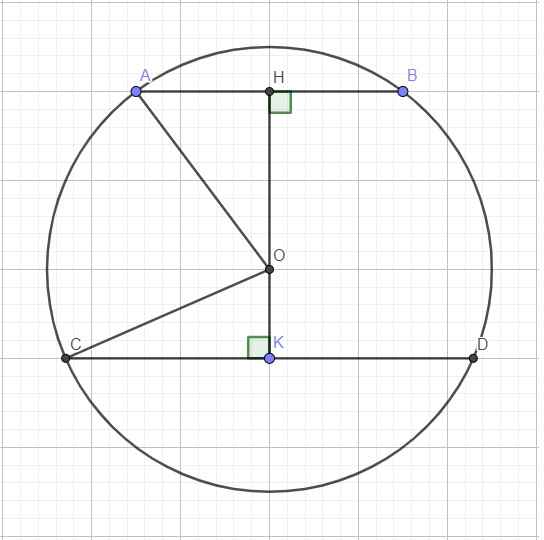
: Cho đường tròn tâm ( O; 5cm ), hai dây AB, CD song song với nhau, có độ dài lần lượt là 8cm và 9,6cm. Tính khoảng cách giữa hai dây đó, biết tâm O nằm trong phần mặt phẳng giới hạn bới hai dây AB và CD.
Từ O kẻ đường thẳng vuông góc AB và CD, cắt AB và CD lần lượt tại H và K
\(\Rightarrow\) H là trung điểm AB và K là trung điểm CD
\(\Rightarrow\left\{{}\begin{matrix}AH=\dfrac{1}{2}AB=4\\CK=\dfrac{1}{2}CD=4,8\end{matrix}\right.\)
Áp dụng định lý Pitago cho tam giác vuông OAH (với chú ý \(OA=OC=R=5\))
\(OH=\sqrt{OA^2-AH^2}=3\left(cm\right)\)
Pitago tam giác OCK:
\(OK=\sqrt{OC^2-CK^2}=1,4\left(cm\right)\)
\(\Rightarrow HK=OH+OK=4,4\left(cm\right)\)
Đúng 1
Bình luận (0)
cho A, B ϵ (O, 5cm) sao cho khoảng cách từ O đến dây AB là 3cm. tính dây AB
Tính chất đường kính và dây cung
\(\Rightarrow\left\{{}\begin{matrix}OH\perp AB\\AH=BH\end{matrix}\right.\)
Theo bài ra ta có: \(\left\{{}\begin{matrix}OH=3cm\\OA=5cm\end{matrix}\right.\)
\(AB=2AH=2\sqrt{5^2-3^2}=2.4=8cm\)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.
Tính khoảng cách từ tâm O đến dây AB.
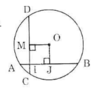
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
![]()
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
Đúng 2
Bình luận (0)
Cho đường tròn tâm o bán kính 5cm khoảng cách từ tâm o đến dây AB=4cm. Tính độ dài dây AB
 ∆OBH vuông tại H
∆OBH vuông tại H
⇒ OB² = OH² + BH² (Pytago)
⇒ BH² = OB² - OH²
= 5² - 4²
= 9
⇒ BH = 3 (cm)
Do OH ⊥ AB
⇒ H là trung điểm của AB
⇒ AB = 2BH = 2.3 = 6 (cm)
Đúng 3
Bình luận (1)
Gọi OH là khoảng cách từ tâm O đến dây AB
=>OH\(\perp\)AB tại H
=>OH=4cm
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(HA^2+4^2=5^2\)
=>\(HA^2=5^2-4^2=9\)
=>HA=3(cm)
H là trung điểm của AB
=>\(AB=2\cdot AH=6\left(cm\right)\)
Đúng 1
Bình luận (0)
(O; 3cm) dây AB=5cm, dây AC=2cm. Tính khoảng cách từ O đến mỗi dây
cho đường tròn tâm o bán kinh 3cm. hai dây cung ab và ac biết rằng ab= 5cm ac=2cm. tính khoảng cách từ o đến mỗi dây cung.
Cho đường tròn tâm O , bán kính R = 5cm , có dây AB = 8cm và M là trung điểm của AB. Tính khoảng cách từ O đến AB?
A. 3cm
B. 4cm
C. 2cm
D. 5 cm
Đáp án A
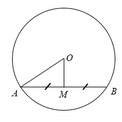
Vì M là trung điểm của AB nên ta có: 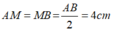
Theo quan hệ vuông góc giữa đường kính và dây ta có:
OM ⊥ AB
Áp dụng định lí Pytago vào tam giác OAM ta có:
O M 2 = O A 2 - A M 2 = 52 - 42 = 9 ⇒ O M = 3 c m
Đúng 1
Bình luận (0)
cho đường tròn tâm o bán kinh 3cm. hai dây cung ab và ac biết rằng ab= 5cm ac=2cm. tính khoảng cách từ o đến mỗi dây cung.
đường tròn (O ; 5cm ) dây AB = 4cm. Khoảng cách từ tâm O đến dây AB bằng?
Khoảng cách từ tâm O đến dây AB là \(\sqrt{5^2-2^2}=\sqrt{25-4}=\sqrt{21}\left(cm\right)\)
Đúng 0
Bình luận (0)