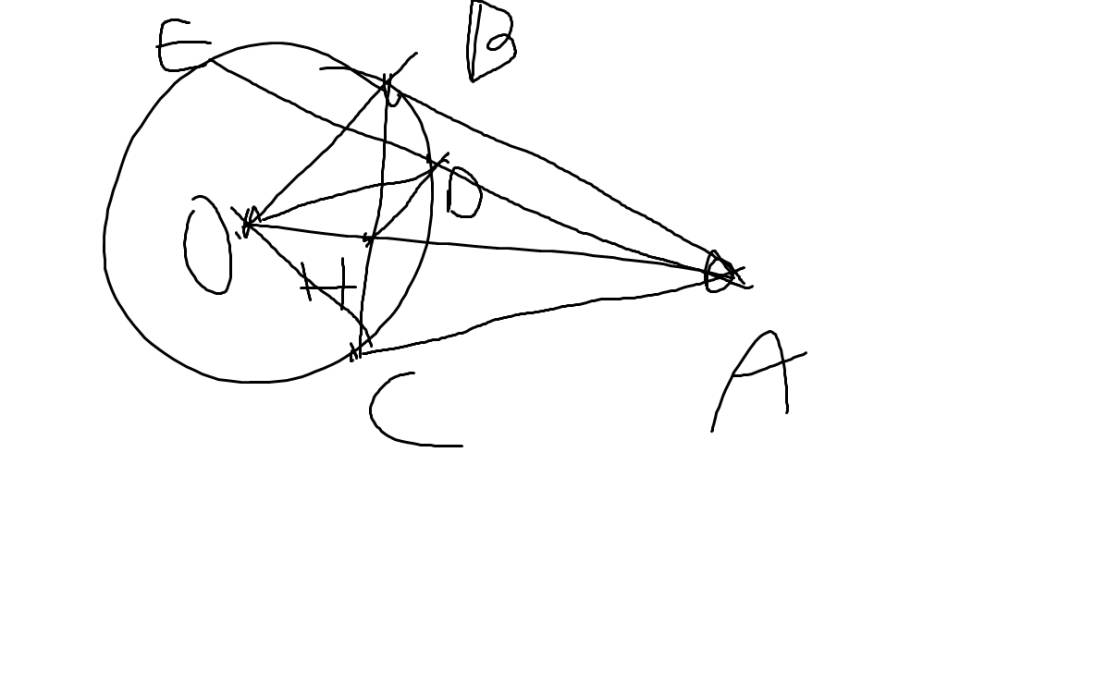
Từ điểm A ở ngoài đường tròn (O;R) kẻ 2 tiếp tuyến AB,AC (với B và C là các tiếp điểm). Kẻ \(BE\perp AC\) và \(CF\perp AB\) (\(E\in AC,F\in AB\)), BE và CF cắt nhau tại H.
a) Chứng minh tứ giác BOCH là hình thoi
b) Chứng minh 3 điểm A,H,O thẳng hàng
c) Xác định vị trí điểm A để H nằm trên (O).

Những câu hỏi liên quan
cho đường tròn (O;R) và đường thẳng a ở ngoài đường thẳng a ở ngoài đường tròn. Gọi OH là khoảng cách từ tâm O đếna và M là một điểm chuyển động trên a. Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (O) , (A,B là 2 tiếp điểm). Gọi D là giao điểm của AB với OH.CMR D là điểm cố định
Trả lời :
Bn Nguyễn Tũn bảo dễ ẹt thì làm đi.
- Hok tốt !
^_^
dễ ẹc thì lm cho mk coi đi
mk ko bt lm
Cho đường tròn O từ điểm A bên ngoài đường tròn, kẽ tiếp tuyến AB, AC đường thẳng qua C // AB cắt đường tròn ở D, AD cắt đường tròn O ở M, CM cắt AB ở N a, góc BAD = góc ACN b, AN2 = NM* NC
a: góc ACN=1/2*sđ cung MC
góc BAD=góc MDC=1/2*sđ cung MC
=>góc ACN=góc BAD
b: Xét ΔNAM và ΔNCA có
góc NAM=góc NCA
góc N chung
=>ΔNAM đồng dạng với ΔNCA
=>NA/NC=NM/NA
=>NA^2=NM*NC
Đúng 0
Bình luận (0)
Từ một điểm a ở bên ngoài đường tròn tâm O,kẻ hai tiếp tuyến AB,AC với đường tròn này
cho đường tròn(o;r), từ điểm a ở bên ngoài đường tròn kẻ 2 tiếp tuyến ab, ac với đường tròn(o) (b,c là tiếp điểm) từ b kẻ đường thẳng song song ac cắt đường tròn(o) tại d(d khác b), đường thẳng ad cắt đường tròn (o) tại e( e khác d) a) chứng minh tứ giác aboc nội tiếp b) chứng minh ab²= ae×ad c) giả sử oa=2r. Tính góc bec và diện tích obac d) so sánh góc cea và góc bec
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 1
Bình luận (0)
Cho đường tròn (O). Từ điểm A bên ngoài đường tròn vẽ 2 tiếp tuyến AB ,AC với đường tròn (B,C là các tiếp điểm).Đường thẳng kẻ qua C song song với AB cắt đường tròn (O) ở D ,AD cắt (O) ở M ,CM cắt AB ở N. Chứng minh:
a) Góc BAD=góc ACN
b)\(^{AN^{ }2}\)=NM.NC
C)N là trung điểm của AB.
Từ điểm A ở bên ngoài đường tròn (O), kẻ 2 tiếp tuyến AB và AC đến đường tròn (O) (B, C là tiếp điểm). Kẻ cát tuyến ADE vs đường tròn (O) (D nằm giữa A và E).
a) Cm: 4 điểm A, B, O, C cùng thuộc một đường tròn
b) Cm OA ⊥ BC tại H và OD² = OH × OA. Từ đó suy ra tam giác OHD đồng dạng vs tam giác ODA.
Giải và vẽ hình giúp mình vớiii !! :(
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,C,O cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
mà OB=OD
nên \(OD^2=OH\cdot OA\)
=>\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
Xét ΔODA và ΔOHD có
\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
\(\widehat{DOA}\) chung
Do đó: ΔODA đồng dạng với ΔOHD
Đúng 1
Bình luận (0)
Từ điểm A ở ngoài đường tròn (O), kẻ 2 tiếp tuyến AB, AC đến đường tròn (O) (B, C là tiếp điểm). Kẻ cát tuyến ADE với đường tròn (O) (D nằm giữa A và E).
a) Cm: 4 điểm A, B, O, C cùng thuộc một đường tròn
b) Cm OA ⊥ BC tại H và OD² = OH × OA. Từ đó suy ra tam giác OHD đồng dạng với tam giác ODA.
--> Cần hình vẽ ạ! (Bài giải e làm r)
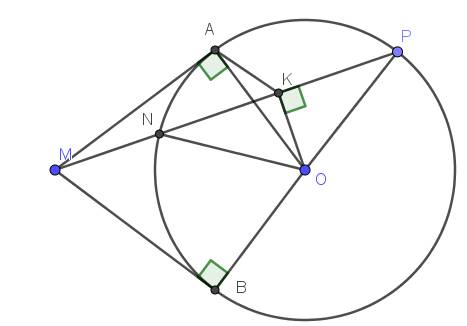
Từ điểm M ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến MA, MB và cát tuyến MNP tới
đường tròn (O); gọi K là trung điểm của NP. Chứng minh rằng: 5 điểm M, A, O, K, B cùng thuộc
1 đường tròn
Lời giải:
Vì $MA,MB$ là tiếp tuyến của $O$ nên $MA\perp OA, MB\perp OB$
$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$
Xét tứ giác $MAOB$ có $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$. Mà 2 góc này đối nhau nên $MAOB$ là tứ giác nội tiếp.
$\Rightarrow M, A,O,B$ cùng thuộc 1 đường tròn (1)
Mặt khác:
Tam giác $ONP$ cân tại $O$ (do $ON=OP=R$) nên trung tuyến $OK$ đồng thời là đường cao.
$\Rightarrow \widehat{MKO}=90^0$
Xét tứ giác $MAKO$ có $\widehat{MAO}=\widehat{MKO}=90^0$. Mà 2 góc này cùng nhìn cạnh $MO$ nên $MAKO$ là tứ giác nội tiếp.
$\Rightarrow M,A,K,O$ cùng thuộc 1 đường tròn (2)
Từ $(1); (2)\Rightarrow M, A, O, K,B$ cùng thuộc 1 đường tròn.
Đúng 0
Bình luận (0)
Từ điểm M ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến MA, MB và cát tuyến MNP tới
đường tròn (O); gọi K là trung điểm của NP. Chứng minh rằng: 5 điểm M, A, O, K, B cùng thuộc
1 đường tròn
Lời giải:
Vì $MA,MB$ là tiếp tuyến của $O$ nên $MA\perp OA, MB\perp OB$
$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$
Xét tứ giác $MAOB$ có $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$. Mà 2 góc này đối nhau nên $MAOB$ là tứ giác nội tiếp.
$\Rightarrow M, A,O,B$ cùng thuộc 1 đường tròn (1)
Mặt khác:
Tam giác $ONP$ cân tại $O$ (do $ON=OP=R$) nên trung tuyến $OK$ đồng thời là đường cao.
$\Rightarrow \widehat{MKO}=90^0$
Xét tứ giác $MAKO$ có $\widehat{MAO}=\widehat{MKO}=90^0$. Mà 2 góc này cùng nhìn cạnh $MO$ nên $MAKO$ là tứ giác nội tiếp.
$\Rightarrow M,A,K,O$ cùng thuộc 1 đường tròn (2)
Từ $(1); (2)\Rightarrow M, A, O, K,B$ cùng thuộc 1 đường tròn.
Đúng 1
Bình luận (0)
Bài 6: (2,5 điểm) Từ điểm A ở ngoài đường tròn (O; R) kẻ tiếp tuyến AB (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). Đoạn AC cắt đường tròn (O) tại điểm D (khác C). a) Chứng minh tam giác BDC vuông và . AC A * B ^ 2 A * O ^ 2 - R ^ 2
b) Qua B kẻ đường thẳng d vuông góc với AO tại H. Đường thẳng d cắt đường tròn (O) tại E (khác B). Gọi F là điểm đối xứng của H qua O. Chứng minh tứ giác CEHF là hình chữ nhật và AE là tiếp tuyến của đường tròn (O; R)
c) Tia CH cắt đường tròn (O) tại G....
Đọc tiếp
Bài 6: (2,5 điểm) Từ điểm A ở ngoài đường tròn (O; R) kẻ tiếp tuyến AB (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). Đoạn AC cắt đường tròn (O) tại điểm D (khác C). a) Chứng minh tam giác BDC vuông và . AC = A * B ^ 2 = A * O ^ 2 - R ^ 2 b) Qua B kẻ đường thẳng d vuông góc với AO tại H. Đường thẳng d cắt đường tròn (O) tại E (khác B). Gọi F là điểm đối xứng của H qua O. Chứng minh tứ giác CEHF là hình chữ nhật và AE là tiếp tuyến của đường tròn (O; R) c) Tia CH cắt đường tròn (O) tại G. Chứng minh HA .HO=HG.HC. Suy ra góc GAB bằng góc EAD
a:
Sửa đề: \(AD\cdot AC=AB^2=AO^2-R^2\)
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)DC tại D
=>BD\(\perp\)CA tại D
Xét ΔBCA vuông tại B có BD là đường cao
nên \(AD\cdot AC=AB^2\left(1\right)\)
Xét ΔOBA vuông tại B có \(OB^2+BA^2=OA^2\)
=>\(BA^2+R^2=OA^2\)
=>\(BA^2=OA^2-R^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AC=AB^2=OA^2-R^2\)
b: ΔOBE cân tại O
mà OH là đường cao
nên H là trung điểm của BE
Xét ΔBCE có
O,H lần lượt là trung điểm của BC,BE
=>OH là đường trung bình của ΔBCE
=>OH//CE và OH=1/2CE
OH//CE
F\(\in\)OH
Do đó: HF//CE
\(OH=\dfrac{1}{2}CE\)
\(OH=\dfrac{1}{2}FH\)
Do đó: CE=FH
Xét tứ giác CEHF có
CE//HF
CE=HF
Do đó: CEHF là hình bình hành
Hình bình hành CEHF có \(\widehat{FHE}=90^0\)
nên CEHF là hình chữ nhật
ΔOBE cân tại O
mà OH là đường cao
nên OH là phân giác của góc BOE
Xét ΔOBA và ΔOEA có
OB=OE
\(\widehat{BOA}=\widehat{EOA}\)
OA chung
Do đó: ΔOBA=ΔOEA
=>\(\widehat{OBA}=\widehat{OEA}=90^0\)
=>AE là tiếp tuyến của (O)
c: Xét (O) có
ΔBGC nội tiếp
BC là đường kính
Do đó: ΔBGC vuông tại G
=>GB\(\perp\)GC tại G
Xét ΔHEC vuông tại E và ΔHGB vuông tại G có
\(\widehat{EHC}=\widehat{GHB}\)
Do đó: ΔHEC đồng dạng với ΔHGB
=>\(\dfrac{HE}{HG}=\dfrac{HC}{HB}\)
=>\(HE\cdot HB=HG\cdot HC\)
=>\(HG\cdot HC=HB^2\left(3\right)\)
Xét ΔBOA vuông tại B có BH là đường cao
nên \(HO\cdot HA=HB^2\left(4\right)\)
Từ (3) và (4) suy ra \(HG\cdot HC=HO\cdot HA\)
Đúng 1
Bình luận (0)