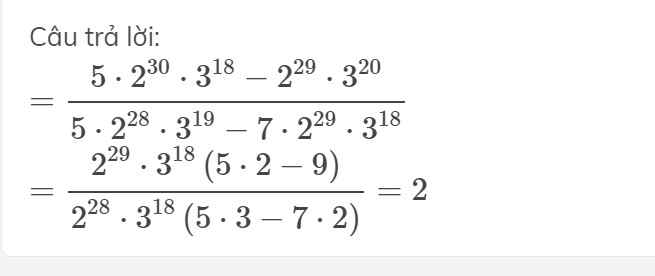\(\dfrac{-19}{2^3.3^2.5}=...\)

Những câu hỏi liên quan
rút gọn phân số ;\(\dfrac{2^3.3^4}{2^2.3^2.5}\)
\(\dfrac{2^3.3^4}{2^3.3^2.5}=\dfrac{1.3^2}{1.1.5}=\dfrac{9}{5}\)
Đúng 0
Bình luận (1)
Ta có :2^3.3^4/2^2.3^2.5=2.3^2/1.1.5=2.9/5=\(\dfrac{18}{5}\)
Đúng 0
Bình luận (0)
Tính \(A=-\frac{19}{2^3.3^2.5}+\left(-3\frac{1}{2}\right)^2:1,2-\left(-1\frac{1}{3}\right)^3:\frac{5}{6}\)
2^3.3/2^2.3^2.5
\(\frac{2^3.3}{2^2.3^2.5}=\frac{2}{3.5}=\frac{2}{15}\)
Đúng 0
Bình luận (0)
\(2^3.\frac{3}{2^2}.3^2.5=8.\frac{3}{4}.9.5=6.9.5=54.5=270\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng:
\(\dfrac{7}{1^3.2^3}+\dfrac{19}{2^3.3^3}+\dfrac{37}{3^3.4^3}+...+\dfrac{29701}{99^3.100^3}< 1\)
\(\dfrac{7}{1^3\cdot2^3}+\dfrac{19}{2^3\cdot3^3}+\dfrac{37}{3^3\cdot4^3}+...+\dfrac{29701}{99^3\cdot100^3}\\ =\dfrac{2^3-1^3}{1^3\cdot2^3}+\dfrac{3^3-2^3}{2^3\cdot3^3}+\dfrac{4^3-3^3}{3^3\cdot4^3}+...+\dfrac{100^3-99^3}{99^3\cdot100^3}\\ =\dfrac{2^3}{1^3\cdot2^3}-\dfrac{1^3}{1^3\cdot2^3}+\dfrac{3^3}{2^3\cdot3^3}-\dfrac{2^3}{2^3\cdot3^3}+...+\dfrac{100^3}{99^3\cdot100^3}-\dfrac{99^3}{99^3\cdot100^3}\\ =\dfrac{1}{1^3}-\dfrac{1}{2^3}+\dfrac{1}{2^3}-\dfrac{1}{3^3}+...+\dfrac{1}{99^3}-\dfrac{1}{100^3}\\ =1-\dfrac{1}{100^3}< 1\)
Vậy ...
Đúng 0
Bình luận (0)
Thực hiện phép tính : \(\dfrac{5.2^{30}.3^{18}-2^3.3^{20}.2^{27}}{5.2^9.2^{19}.3^{19}-7.2^{29}.3^{18}}\)
Rút gọn:
2^3.3/2^2.3^2.5
muốn rút gọn phân số đó ta làm như sau:
\(\frac{2^3\cdot3}{2^2\cdot3^2\cdot5}\)=\(\frac{2}{3\cdot5}\)=\(\frac{2}{15}\)
Đúng 0
Bình luận (0)
1.Quy đồng mẫu và so sánh:
a, -8/31 và -789/3131
b,11/2^3.3^4.5^2 và 29/2^2.5^4.5^2
c,7/39, 11/65 và 9/52
d,17/20, -19/30, 38/45, -13/18
Tính kết quả của các phép tính với lũy thừa sau : ( Dấu ( . ) là dấu nhân nhé ! )
\(3^4:3^2=..................................\)
\(3^3.3^4=....................................\)
\(5^2.5^5=.....................................\)
\(19^{14}:19^7=......................................\)
34: 32= 34- 2= 32= 9.
33. 34= 33+ 4= 37= 2187.
52. 55= 52+ 5= 57= 78125.
1914: 197= 1914- 7= 197= 893871739.
Đúng 0
Bình luận (0)
+) \(3^4:3^2=3^{4-2}=3^2\)
+) \(3^3\times3^4=3^{3+4}=3^7\)
+) \(5^2\times5^5=5^{2+5}=5^7\)
+) \(19^{14}:19^7=19^{14-7}=19^7\)
_Chúc bạn học tốt_
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) 2^3.3^4/2^2.3^2.5 ; 2^4.5^2.11^2.7/2^3.5^3.7^2.11
Ta có:
\(\frac{2^3.3^4}{2^2.3^2.5}=\frac{2.3^2}{5}=\frac{18}{5}\)
\(\frac{2^4.5^2.11^2.7}{2^3.5^3.7^2.11}=\frac{2.11}{5.7}=\frac{22}{35}\)
rút gọn: \(\frac{2^3.3^4}{2^2.3^2.5}\)
Ta có:
\(\frac{2^2.2.3^2.3^2}{2^2.3^2.5}\) =\(\frac{2.3^2}{5}\) =\(\frac{18}{5}\)
Vậy
Đúng 0
Bình luận (0)
Ta cã: \(\frac{2^3.3^4}{2^2.3^2.5}\)
\(=\frac{2^2.2.3^2.3^2}{2^2.3^2.5}\)
\(=\frac{2.3^2}{5}\)
\(=\frac{18}{5}\)
Đúng 0
Bình luận (0)