. Cho tam giác ABC vuông tại A . Vẽ AH vuông góc với BC tại H . Trên tia đối của tia HA lấy điểm M sao cho HM=HA . CHứng minh rằng :
a) tam giác AHB = tam giác MHB
b) tam giác MBC là tam giác vuông
Cho tam giác ABC , từ A kẻ AH vuông góc với BC (H thuộc BC). Trên tia đối của tia HA lấy điểm M sao cho HA = HM . Chứng minh rằng:
a) Tam giác AHC = Tam giác MHC
b) Tam giác ABC = Tam giác MBC
Mình cần gấp
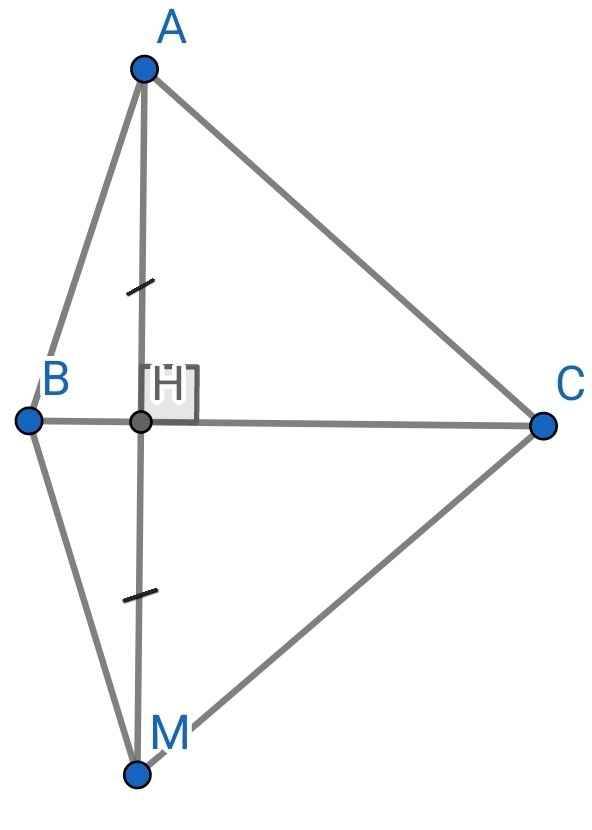 a) Xét hai tam giác vuông: ∆AHC và ∆MHC có:
a) Xét hai tam giác vuông: ∆AHC và ∆MHC có:
HC là cạnh ccung
AH = MH (gt)
⇒ ∆AHC = ∆MHC (hai cạnh góc vuông)
b) Do ∆AHC = ∆MHC (cmt)
⇒ ∠ACH = ∠MCH (hai góc tương ứng)
AC = MC (hai cạnh tương ứng)
Do ∠ACH = ∠MCH (cmt)
⇒ ∠ACB = ∠MCB
Xét ∆ABC và ∆MBC có:
AC = MC (cmt)
∠ACB = ∠MCB (cmt)
BC là cạnh chung
⇒ ∆ABC = ∆MBC (c-g-c)
Cho tam giác ABC cân tại A.Kẻ AH vuông góc BC tại H .Trên tia đối của HA lấy điểm M sao cho AH=HM. a) Chứng minh tam giác ABH=tam giác MBH. b) Trên tia đối của tia CA lấy điểm N sao cho CA=CN.Chứng minh tam giác CMN cân. c) Chứng minh AM vuông góc với MN.
a,Ta có:
\(AH\perp BC\) nên \(\widehat{AHB}\) +90 độ.
Vì M là tia đối của HA nên \(\widehat{MHB}\)= 90 độ.
Xét \(\Delta ABH\) và \(\Delta MBH\)có
AH = MH (gt)
\(\widehat{AHB}\) = \(\widehat{MHB}\) (= 90 độ )
BH : cạnh chung
\(\Rightarrow\Delta ABH=\Delta MBH\)( c.g.c )
b,Xét \(\Delta AHCv\text{à}\Delta MHC\)Ta có:
AH = HM (gt)
\(\widehat{AHC}\)= \(\widehat{MHC}\)(= 90 độ)
HC : cạnh chung
\(\Rightarrow\Delta AHC=\Delta MHC\)( c.g.c)
\(\Rightarrow\)AC=CM ( t/ứ)
Mà AC = CN (gt) và CM = AC (cmt)
nên CM = CN
\(\Rightarrow\Delta CMN\)cân
Cho tam giác ABC nhọn có AB=AC. Gọi H là trung điểm BC
a) Chứng minh tam giác AHB = tam giác AHC và AH vuông tại BC.
b) Trên tia đối của tia HA lấy điểm M sao cho HM=HA .Chứng minh tam giác AHB = tam giác MHC và MC // AB
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
Do đó: ΔABH=ΔACH
Cho tam giác ABC cân tại A vẽ AH vuông góc với BC ( H thuộc BC)
a) Chứng minh tam giác AHB bằng tam giác AHC?
b) Trên tia đối tia HA lấy điểm D sao cho HA=HD, chứng minh tam giác ACD cân tại C?
c) Chứng minh: HA < 1/2( AC + CD)
a) Xét tam giác ABC cân tại A: AH là đường cao (AH vuông góc với BC)
=> AH là đường trung tuyến (TC tam giác cân)
=> H à TĐ của BC
=> BH = HC
Xét tam giác AHB và tam giác AHC:
BH = HC (cmt)
^AHB = ^AHC (90o)
AH chung
=> tam giác AHB = tam giác AHC (ch - cgv)
b) Ta có: HA = HD (gt) => H là TĐ của AD
Xét tam giác ACD có:
CH là đường cao (CH vuông góc AD)
CH là trung tuyến (H là TĐ của AD)
=> tam giác ACD cân tại C
c) Xét tam giác ACD cân tại A có:
AD > AC + CD (Bất đẳng thức trong tam giác)
=> \(\dfrac{1}{2}AD=\dfrac{1}{2}\left(AC+CD\right)\)
Mà \(HA=\dfrac{1}{2}AD\) (H là TĐ của AD)
=> \(HA>\dfrac{1}{2}\left(AC+CD\right)\) (ĐPCM)
Cho tam giác ABC có AB = AC và AC > BC> Gọi H là trung điểm cạnh BC
a) Chứng minh : tam giác AHB = tam giác AHC
b) Trên tia đối của tia HA lấy điểm M sao cho HM = HA. CMR AB//MC
c) Từ B vẽ đường thẳng vuông góc với AC tại K, trên tia đối của tia KC lấy điểm D sao cho KD = KC. Chứng minh : Bk là tia phân giác của góc DBC
d) Trên tia đối của tia BA lấy điểm E sao cho BE = AD. Chứng minh CE = CA
a: Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
b: Xét tứ giác ABMC có
H là trung điểm của AM
H là trung điểm của BC
Do đó: ABMC là hình bình hành
Suy ra: AB//MC
Cho tam giác ABC có 3 góc nhọn, đường cao AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD.
a) Chứng minh: tam giác AHB = tam giác DHB
b) Chứng minh rằng: BC là tia phân giác của góc ABD
c) Gọi M là trung điểm của Bc. Trên tia đối của tia MA lấy điểm F sao cho MF = MA. Từ F kẻ FN vuông góc với BC (N thuộc BC). Chứng minh: HD = NF
a) Xét \(\Delta\)AHB và \(\Delta\)DHB có:
^AHB = ^DHB ( 1v )
HA = HD ( giả thiết )
MH chung
=> \(\Delta\)AHB = \(\Delta\)DHB ( c.g.c)
b) Từ (a) => ^ABH = ^DHB => BH là phân giác ^ABD
Vì \(\Delta\)ABC nhọn => H nằm trong đoạn BC
=> BC là phân giác ^ABD
c) NF vuông BC
AH vuông BC
=> NF // AH
=> ^NFM = ^HAM ( So le trong )
Lại có: ^HMA = NMF ( đối đỉnh ) và MA = MF ( giả thiết )
=> \(\Delta\)NFM = \(\Delta\)HAM ( g.c.g)
=> NF = AH ( 2)
Từ ( a) => AH = HD ( 3)
Từ (2) ; (3) => NF = HD
Cho tam giác ABC vuông góc tại A. Vẽ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD.
a, Cho BH = 4cm, HA = 3cm. Tính AB.
b, Chứng minh tam giác AHC = tam giác DHC. Từ đó chứng minh tam giác ACD cân.
c, Chứng minh tam giác BDC vuông
a: \(AB=\sqrt{BH^2+AH^2}=5\left(cm\right)\)
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
HC chung
HA=HD
Do đó:ΔAHC=ΔDHC
Suy ra: AC=DC
hay ΔACD cân tại C
c: Xét ΔBAD có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔABD cân tại B
Xét ΔBAC và ΔBDC có
BA=BD
AC=DC
BC chung
Do đó: ΔBAC=ΔBDC
Suy ra: \(\widehat{BAC}=\widehat{BDC}=90^0\)
hayΔBDC vuông tại D
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H thuộc BC)
a) Chứng minh tam giác AHB = tam giác AHC
b) Giả sử AB=AC=5cm, BC=8cm. Tính AH
c) Trên tia đối của tia HA lấy điểm M sao cho HM=HA. Chứng minh tam giác ABM cân
d) Chứng minh BM//AC
(Bạn tự vẽ hình giùm)
a/ \(\Delta AHB\)vuông và \(\Delta AHC\)vuông có: AB = AC (\(\Delta ABC\)cân tại A)
Cạnh AH chung
=> \(\Delta AHB\)vuông = \(\Delta AHC\)vuông (cạnh huyền - cạnh góc vuông) (đpcm)
b/ Ta có \(\Delta AHB\)= \(\Delta AHC\) (cm câu a) => HB = HC (hai cạnh tương ứng) => H là trung điểm của BC
=> BH = \(\frac{BC}{2}\)= \(\frac{8}{2}\)= 4 (cm)
Ta có \(\Delta AHB\)vuông tại H => AH2 + HB2 = AB2 (định lí Pitago)
=> AH2 = AB2 - HB2
=> AH2 = 52 - 42
=> AH2 = 25 - 16
=> AH2 = 9
=> AH = \(\sqrt{9}\)
=> AH = 3
c/ \(\Delta AHB\)vuông tại H và \(\Delta MHB\)vuông tại H có: AH = MH (gt)
Cạnh HB chung
=> \(\Delta AHB\)vuông = \(\Delta MHB\)vuông (cạnh huyền - cạnh góc vuông) => AB = MB (hai cạnh tương ứng)
=> \(\Delta ABM\)cân tại B (đpcm)
d/ Ta có \(\Delta AHB\)= \(\Delta AHC\)(cm câu a) => \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng) (1)
Ta có \(\Delta AHB\)= \(\Delta MHB\)(cm câu c) => \(\widehat{M}=\widehat{BAH}\)(hai góc tương ứng) (2)
Từ (1) và (2) => \(\widehat{M}=\widehat{CAH}\)ở vị trí so le trong => BM // AC (đpcm)
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H
a/ Chứng minh :tam giác AHB = tam giác AHCvà AH là tia phân giác của góc BAC
b/ Từ H kẻ HM vuông góc với AB, HN vuông góc với AC ,AH cắt MN tại K. Chứng minh AH vuông góc với MN
c/ Trên tia đối của tia HM lấy P sao cho H là trung điểm của MP, NP cắt BC tại E, NH cắt ME tại Q. Chứng minh: P, Q, K thẳng hàng.
a,Ta có: tam giác ABC cân tại A
=>AB=AC
Xét tam giác AHB và tam giác AHC có:
góc AHB=góc AHC=90 độ
AB=AC(cmt)
AH chung
=>tam giác AHB=tam giác AHC(cạnh huyền-cạnh góc vuông)
=>góc BAH=góc CAH(2 góc tương ứng)
=>AH là tia phân giác của góc BAC
(bít lm mỗi câu a, thông cảm)