cho tam giác nhọn ABC, trực tâm H. Gọi K là điểm đối xứng với H qua BC. chứng minh BAH=BCK

Những câu hỏi liên quan
Cho tam giác nhọn ABC có ∠ A = 60 0 , trực tâm H. Gọi M là điểm đối xứng với H qua BC. Chứng minh ∆ BHC = ∆ BMC
Vì M đối xứng với H qua trục BC
⇒ BC là đường trung trực của HM
⇒ BH = BM (t/chất đường trung trực)
CH = CM (t/chất đường trung trực)
Xét tam giác BHC và tam giác BMC có:
BC chung
BH= BM ( chứng minh trên)
CH = CM (chứng minh trên)
Suy ra: ∆ BHC = ∆ BMC (c.c.c)
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có trực tâm H. Gọi I là trung điểm BC và K đối xứng với H qua I. Chứng minh bốn điểm A, B, C, K cùng thuộc một đường tròn.
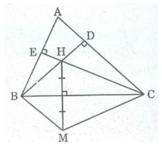
Cho tam giác ABC nhọn (AB<AC), trực tâm H. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M. Gọi I là điểm đối xứng với H qua BC.
a) Chứng minh tứ giác BIKC là hình thang cân.
b) BK cắt HI tại G. Tìm điều kiện của tam giác ABC để tứ giác GHCK là hình thang cân.
a) Giao điểm của AH và BC là E. Dễ thấy: \(\Delta\)BHM = \(\Delta\)CKM (c.g.c) => ^HBM = ^KCM
=> ^HBC = ^KCB. Do H đối xứng với I qua BC => ^HBC = ^IBC => ^KCB = ^IBC (1)
Xét \(\Delta\)HIK: E là trung điểm IH; M là trung điểm của HK => EK là đường trung bình \(\Delta\)HIK
=> EM // IK hay IK // BC => Tứ giác BIKC là hình thang (2)
Từ (1) & (2) => Tứ giác BIKC là hình thang cân (đpcm).
b) Dễ c/m tứ giác BHCK là hình bình hành (Do có tâm đối xứng) => HC // BK
Hay HC // GK => Tứ giác GHCK là hình thang
Để tứ giác GHCK là hình thang cân thì ^GHC = ^KCH
<=> ^HAC + ^HCA = ^HCB + ^HBC <=> ^HCA = ^HCB ( Vì ^HAC = ^HBC, cùng phụ ^ACB)
<=> CH là phân giác ^ACB. Mà CH cũng là đường cao của \(\Delta\)ABC => \(\Delta\)ABC cân tại C
Vậy khi \(\Delta\)ABC cân tại C thì tứ giác GHCK là hình thang cân.
Đúng 0
Bình luận (0)
cho tam giác abc nhọn .vẽ các đường cao bd ce gọi h là trực tâm của tam giác abc .a)chưng minh tứ giác bedc nội tiếp. b) gọi m là điểm đối xứng h qua bc chứng minh tứ giác abmc nội tiếp. c) gọi n là điểm đối xứng của h qua trung điểm I của bc chứng minh abnc nội tiếp
a: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
b: góc HBC+góc HCB=90 độ-góc ABC+90 độ-góc ACB
=góc BAC
=>góc BHC=180 độ-góc BAC
=>góc BHC+góc BAC=180 độ
H đối xứng M qua BC
=>BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
=>ΔBHC=ΔBMC
=>góc BMC=góc BHC
=>góc BMC+góc BAC=180 độ
=>ABMC nội tiếp
c: Xét tứ giác BHCN có
BC cắt HN tại trung điểm của mỗi đường
=>BHCN là hìnhbình hành
=>góc BHC=góc BNC
=>góc BNC+góc bAC=180 độ
=>ABNC nội tiếp
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, H là trực tâm và E là trung điểm của BC. Gọi I là điểm đối xứng với H qua E. H a) Chứng minh tứ giác BHCI là hình bình hành. b) Chứng minh: BỊ AB c ) Gọi O là giao điểm của các đường trung trực của tam giác ABC . Chứng minh A đối xứng với I qua O
a: Xét tứ giác BHCI có
E là trung điểm của BC
E là trung điểm của HI
Do đó: BHCI là hình bình hành
Đúng 0
Bình luận (0)
Bài 1.Cho tam giác nhọn ABC, trực tâm H. Gọi K là điểm đối xứng với H qua BC.
a) Chứng minh hai tam giác BHC và BKC bằng nhau.
b) Cho góc BAC=70 độ. Tính số đo góc BKC
a) Ta có:
K đối xứng với H qua BC
⇒ BC là trung trực của HK
⇒ BH=BK; CH=CK
Xét ΔBHC và ΔBKC có:
BH=BK (cmt)
CH=CK (cmt)
BC: cạnh chung
Do đó ΔBHC = ΔBKC(c.c.c)
b) Ta có:
ˆBHK = ˆBAH + ˆABH (góc ngoài của ΔABH)
ˆCHK = ˆCAH+ ˆACH (góc ngoài của ΔACH)
⇒ ˆBHC = ˆBHK + ˆCHK
= ˆBAH + ˆABH + ˆCAH + ˆACH
= ˆBAC + ˆABH + ˆACH
Ta lại có:
ˆBAC+ˆABH = 90o (BH⊥AC)
ˆBAC+ˆACH = 90o (CH⊥AB)
⇒2ˆBAC+ˆABH+ˆACH=180o
⇒ˆABH+ ˆACH = 180o− 2ˆBAC
Do đó:
ˆBHC =ˆBAC+ 180o− 2ˆBAC= 180o− ˆBAC= 180o−70o = 110o
Mặt khác:
ˆBHC = ˆBKC (ΔBHC = ΔBKC)
⇒ˆBKC=110
Đúng 2
Bình luận (0)
Cho tam giác ABC nhọn, trực tâm H. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M
a/ Tứ giác BHCK là hình gì? Vì sao?
b/ Chứng minh tam giác ABK vuông
Giúp mik với mik cần gấp lắm làm ơn
Vẽ hình không chuẩn => không chắc câu a lắm nha!
Đúng 1
Bình luận (0)
Cho tam giác ABC, O là giao của 3 đường trung trực, H là trực tâm của tam giác M là trung điểm của BC. Gọi K là điểm đối xứng của H qua M. Chứng minh A và K đối xứng với nhau qua O
Giúp mình nha
tam giác abc nhọn. h là trực tâm của tam giác. k đối xứng với h qua bc. chứng minh: tam giác bhc=tam giác bkc



















