Đưa thừa số ra ngoài dấu căn
a) \(\sqrt{-9b^3}\) với b ≤ 0
b) \(\sqrt{24a^4b^8}\) với a,b ∈ R

Những câu hỏi liên quan
B1 . Đưa thừa số ra ngoài dấu căn : a. √5a² ( với a ≤ 0) b. √9b³ ( với b ≤ 0 ) c. √72a²b⁴ ( với a < 0 ) d . √24a⁴b⁸ ( a , b € R ) Giúp mình với ạ
a: \(\sqrt{5a^2}=\left|a\sqrt{5}\right|=-a\sqrt{5}\left(a< =0\right)\)
c: A=\(\sqrt{72a^2b^4}=\sqrt{36a^2b^4\cdot2}=6\sqrt{2}\cdot b^2\cdot\left|a\right|\)
mà a<0
nên \(A=-6\sqrt{2}\cdot ab^2\)
d: \(\sqrt{24a^4b^8}=\sqrt{4a^4b^8\cdot6}=2a^2b^4\cdot\sqrt{6}\)
Đúng 1
Bình luận (0)
Đưa thừa số ra ngoài dấu căn
a.
\(\left(\sqrt{28}-5\sqrt{35}+7\sqrt{112}\right)2\sqrt{7}\)
b. \(\left(\sqrt{72}-3\sqrt{24}+5\sqrt{8}\right)\sqrt{2}+4\sqrt{27}\)
a) \(\left(\sqrt{28}-5\sqrt{35}+7\sqrt{112}\right)2\sqrt{7}=2\sqrt{196}-10\sqrt{245}+14\sqrt{784}\)
\(=28-10\sqrt{49.5}+392=420-70\sqrt{5}\)
b) \(\left(\sqrt{72}-3\sqrt{24}+5\sqrt{8}\right)\sqrt{2}+4\sqrt{27}=\sqrt{144}-3\sqrt{48}+5\sqrt{16}+4\sqrt{9.3}\)
\(=12-3\sqrt{16.3}+20+12\sqrt{3}=32-12\sqrt{3}+12\sqrt{3}=32\)
Đúng 2
Bình luận (0)
Khử mẫu của biểu thức dưới dấu căn bậc hai
a) \(\sqrt{\dfrac{5x^3}{49y}}\)
với x ≥ 0, y >0
b) 7xy\(\sqrt{\dfrac{-3}{xy}}\)
với x<0, y>0
baif1 so sánh số hữa tỉ a phần b [a,b thuoc z , b khác o ] với số 0 khi a,b cùng dấu và khi a,b khác dấu.
+ Nếu a và b cùng dấu thì a/b dương => a/b > 0
+ Nếu a và b khác dấu thì a/b âm => a/b < 0
Đúng 0
Bình luận (0)
RÚT GỌN BIỂU THỨC Afrac{a-b}{sqrt{a}-sqrt{b}}-frac{sqrt{a^3}-sqrt{b^3}}{a-b}(với a_ 0, b_ 0, a#b)Bleft(frac{sqrt{x^3}+sqrt{y^3}}{sqrt{x}+sqrt{y}}-sqrt{xy}right).left(frac{sqrt{x}+sqrt{y}}{x-y}right)(với x_ 0, y_ 0, x#y)Cx-4-sqrt{16-8x^2+x^4}(với x4)Dfrac{a+b-2sqrt{ab}}{sqrt{a}-sqrt{b}}:frac{1}{sqrt{a}+sqrt{b}}(với a0, b0, a#b)Eleft(2+frac{a-sqrt{a}}{sqrt{a}-1}right).left(2-frac{a+sqrt{a}}{sqrt{a}+1}right)(với a0, a#1)Ffrac{a-3sqrt{a}}{sqrt{a}-3}-frac{a+4sqrt{a}+3}{sqrt{a}+3}( với a_ 9...
Đọc tiếp
RÚT GỌN BIỂU THỨC
A=\(\frac{a-b}{\sqrt{a}-\sqrt{b}}-\frac{\sqrt{a^3}-\sqrt{b^3}}{a-b}\)(với a>_ 0, b>_ 0, a#b)
B=\(\left(\frac{\sqrt{x^3}+\sqrt{y^3}}{\sqrt{x}+\sqrt{y}}-\sqrt{xy}\right).\left(\frac{\sqrt{x}+\sqrt{y}}{x-y}\right)\)(với x>_ 0, y>_ 0, x#y)
C=\(x-4-\sqrt{16-8x^2+x^4}\)(với x>4)
D=\(\frac{a+b-2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}:\frac{1}{\sqrt{a}+\sqrt{b}}\)(với a>0, b>0, a#b)
E=\(\left(2+\frac{a-\sqrt{a}}{\sqrt{a}-1}\right).\left(2-\frac{a+\sqrt{a}}{\sqrt{a}+1}\right)\)(với a>0, a#1)
F=\(\frac{a-3\sqrt{a}}{\sqrt{a}-3}-\frac{a+4\sqrt{a}+3}{\sqrt{a}+3}\)( với a>_ 9)
G=\(\frac{9-x}{\sqrt{x}+3}-\frac{9-6\sqrt{x}+x}{\sqrt{x}-3}-6\)( với x>_ 9 )
Rút gọn:
a/ \(\frac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\frac{1}{\sqrt{a}-\sqrt{b}}\) (a,b>0,a#b)
b/(1+ a+căna/căna +1).(1- a.căna/căna -1) (a>=0,a#1)
a)\(\frac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\frac{1}{\sqrt{a}-\sqrt{b}}\)
b) \(\left(\frac{1+a+\sqrt{a}}{\sqrt{a}+1}\right).\left(\frac{1-a-\sqrt{a}}{\sqrt{a}-1}\right)\)
thế này à
Đúng 0
Bình luận (0)
Tìm GTLN của
\(P=\dfrac{a}{\sqrt{1+2bc}}+\dfrac{b}{\sqrt{1+2ca}}+\dfrac{c}{\sqrt{1+2ab}}\)
với a,b,c là các số lớn hơn 0 thỏa mãn điều kiện : \(a^2+b^2+c^2=1\)
P=\(\dfrac{\sqrt{2}.a}{\sqrt{\left(a^2+\left(b+c\right)^2\right)\left(1+1\right)}}+\dfrac{\sqrt{2}.b}{\sqrt{\left(b^2+\left(a+c\right)^2\right)\left(1+1\right)}}+\dfrac{\sqrt{2}.c}{\sqrt{\left(c^2+\left(b+a\right)^2\right)\left(1+1\right)}}\)>=\(\dfrac{\sqrt{2}.a}{\sqrt{\left(a+b+c\right)^2}}+\dfrac{\sqrt{2}.b}{\sqrt{\left(a+b+c\right)^2}}+\dfrac{\sqrt{2}.c}{\sqrt{\left(a+b+c\right)^2}}\)>=\(\sqrt{2}\)
Đúng 0
Bình luận (0)
nhầm dấu tí là dấu lớn hơn bằng còn cách lm thì đúng nhé
Đúng 0
Bình luận (0)
Bài 20 (trang 15 SGK Toán 9 Tập 1)
Rút gọn các biểu thức sau:
a) $\sqrt{\dfrac{2a}{3}}.\sqrt{\dfrac{3a}{8}}$ với $a\ge 0$ ; b) $\sqrt{13a}.\sqrt{\dfrac{52}{a}}$ với $a>0$ ;
c) $\sqrt{5a}.\sqrt{45a}-3a$ với $a\ge 0$ ; d) $(3-a)^2-\sqrt{0,2}.\sqrt{180a^2}$.
a, \(\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\left|\frac{a}{2}\right|=\frac{a}{2}\)
do \(a\ge0\)
b, \(\sqrt{13a}.\sqrt{\frac{52}{a}}=\sqrt{\frac{676a}{a}}=\sqrt{676}=26\)
c, \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\left|15a\right|-3a\)
\(=15a-3a=12a\)do a > 0
d, \(=\left(3-a\right)^2-\sqrt{0,2}.\sqrt{180a^2}\)
\(=\left(3-a\right)^2-\sqrt{36a^2}=\left(3-a\right)^2-\left|6a\right|\)
Với \(a\ge0\Rightarrow\left(3-a\right)^2-6a=a^2-6a+9-6a=a^2-12a+9\)
Với \(a< 0\Rightarrow\left(3-a\right)^2+6a=a^2-6a+9+6a=a^2+9\)
a) Ta có:
b) Ta có:
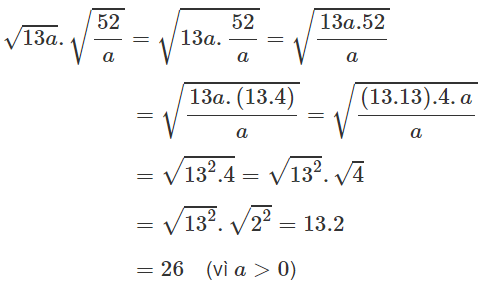
c) Do a ≥ 0 nên bài toán luôn xác định. Ta có:
d) Ta có:
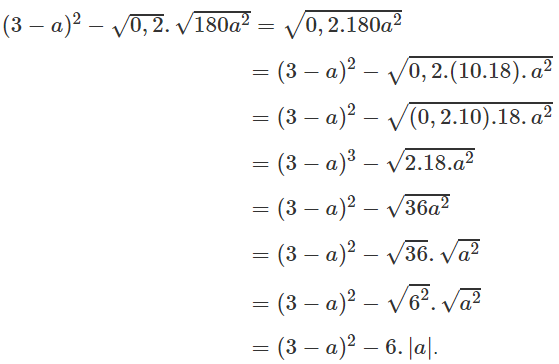
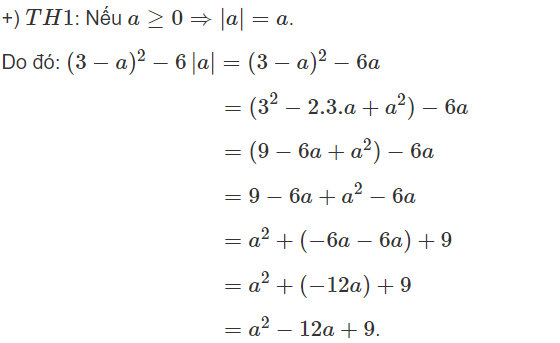
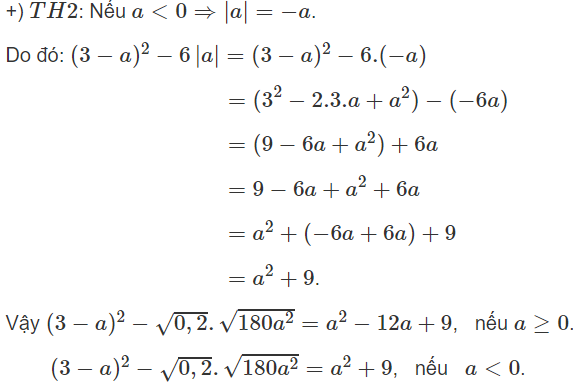
b) \(\sqrt{13a}\).\(\sqrt{\frac{52}{a}}\)=\(\sqrt{13a.\frac{52}{a}}\)=\(\sqrt{13.13.2.2}\)=13.2=26
Xem thêm câu trả lời
Tinh \(\sqrt{3}\) với 18 chữ số thập phân sau dấu phẩy (toán casio)
Giúp mình mấy bài này với ạ:
1/ Tìm số hạng lớn nhất của dãy số \(_{u_n}\) với \(u_n=\frac{n-1}{n^2-n+7}\)
2/ Cho dãy số \(u_n=\sqrt{2+\sqrt{2+\sqrt{2+...+\sqrt{2}}}}\)( n dấu căn )
a) Chứng mình \(u_n=2\cos\frac{\pi}{2^{n+1}}\)
b) Xét tình đơn điệu và chứng minh dãy số trên bị chặn.




























