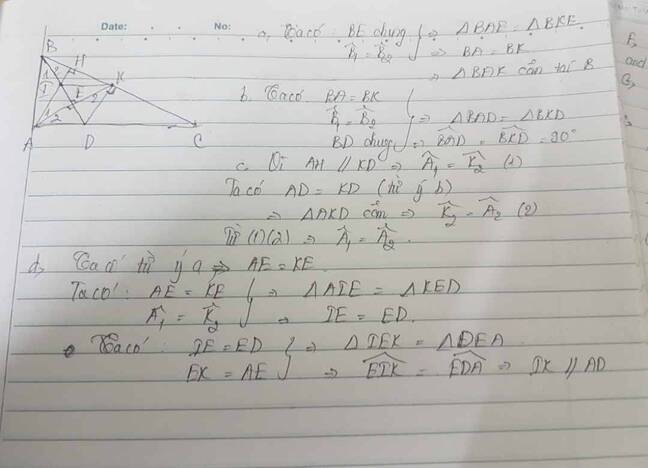cho tam giacs ABC và tam giác tam giác ABC= tam giác DEF kẻ AH vuông góc với BC [ H THUỘC BC] và kẻ DK vuông góc với EF . chứng minh rằng AH =DK

Những câu hỏi liên quan
cho tam giác ABC , tam giác ABC = tam giác DEF , kẻ AH vuông góc với BC [H thuộc BC ] . kẻ DK vuông góc với EF [K thuộc EF ] . chứng minh rằng AH=DK
Xét $\triangle{ABH}$ và $\triangle{DEK}$
$AB = DE$ và $\widehat{ABH} = \widehat{DEK}$ ($\triangle{ABC} =\triangle{DEF}$)
$\widehat{AHB} = \widehat{DKE} ( = 90^\circ)$
$\implies \triangle{ABH} = \triangle{DEK}$ (ch-gn)
$\implies AH = DK$
Đúng 0
Bình luận (2)
cho tam giác ABC , tam giác ABC = tam giác DEF . kẻ AH vuông góc với BC [H thuộc BC] , kẻ DK vuông góc với EF [ K thuộc EF ]. chứng minh rằng AH =DK
Cho tam giác nhọn ABC và tam giác ABC=tam giác DEF. Kẻ AH vuông góc với BC ( H thuộc BC ) và DK vuông góc với EF ( K thuộc EF ). Chứng minh rằng AH=DK
Cho tam giacs nhịn ABC và tam giác ABC bằng tam giác DEF . Kẻ AH vuông góc BC ( H thuộc BC) và Dk Vuông góc EF (k thuộc EF).CMR AH=DK
Xem chi tiết
Ai đi qa để lại cko e cái câu tl vs ạ
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC), kẻ AH vuông góc với BC, D thuộc AC sao cho AB=AD kẻ DK vuông góc với AH tại K. Cần chứng minh a) Tam giác ABH= tam giác DAK b) So sánh BH và AD
a: Xét ΔABH vuông tại H và ΔDAK vuông tại K có
AB=DA
góc ABH=góc DAK
=>ΔABH=ΔDAK
b: ΔABH=ΔDAK
=>BH=AK
mà AK<AD
nên BH<AD
Đúng 1
Bình luận (0)
1.Cho tam giác ABC có AB3cm,AC4cm,BC5cma) Chứng tỏ tam giác ABC vuông tại A.b) Trên tia đối của tia AC lấy điểm D sao cho CD6cm.Tính độ dài đoạn thẳng BD.2.Cho tam giác ABC, biết AB 12cm,AC 9cm,BC 15cm.a) Chứng tỏ tam giác ABC vuông.b) Kẻ AH vuông góc với BC tại H, biết AH 7,2cm.Tính độ dài đoạn thẳng BH và HC.3.Cho tam giác nhọn ABC(ABAC). Kẻ AH vuông góc với BC tại H. Tính chu vi tam giác ABC biết AC 20cm, AH 12cm, BH 5cm.4.Cho tam giác ABC cân tại A, kẻ AH vuông góc với BCa) Chứng minh...
Đọc tiếp
1.Cho tam giác ABC có AB=3cm,AC=4cm,BC=5cm
a) Chứng tỏ tam giác ABC vuông tại A.
b) Trên tia đối của tia AC lấy điểm D sao cho CD=6cm.Tính độ dài đoạn thẳng BD.
2.Cho tam giác ABC, biết AB = 12cm,AC = 9cm,BC = 15cm.
a) Chứng tỏ tam giác ABC vuông.
b) Kẻ AH vuông góc với BC tại H, biết AH = 7,2cm.Tính độ dài đoạn thẳng BH và HC.
3.Cho tam giác nhọn ABC(AB<AC). Kẻ AH vuông góc với BC tại H. Tính chu vi tam giác ABC biết AC = 20cm, AH = 12cm, BH = 5cm.
4.Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC
a) Chứng minh tam giác AHB = tam giác AHC
b) Từ H kẻ HM vuông góc với AB tại M. Trên cạnh AC lấy điểm N sao cho BM = CN. Chứng minh HN vuông góc AC.
5.Cho tam giác ABC cân tại A, tia phân giác của góc A cắt BC tại I
a) Chứng minh tam giác AIB = tam giác AIC
b) Lấy M là trung điểm AC. Trên tia đối của tia MB lấy điểm D sao cho MB = MD. Chứng minh AD song song BC và AI vuông góc AD.
c) Vẽ AH vuông góc BD tại H, vẽ CK vuông góc BD tại K. Chứng minh BH = DK.
6.Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc BD(E thuộc BD). AE cắt BC ở K.
a) Chứng minh tam giác ABE = tam giác KBE và suy ra tam giác BAK cân.
b) Chứng minh tam giác ABD = tam giác KBD và DK vuông góc BC.
c) Kẻ AH vuông góc BC(H thuộc BC). Chứng minh AK là tia phân giác của HAC.
Mọi người vẽ hình lun 6 bài giúp mình nha! Mình đang cần gấp!:(
Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
a) Áp dụng định lý Pytago vào \(\Delta\)ABC có
AB2+AC2=BC2
thay AB=3cm, AC=4cm va BC=5cm, ta có:
32+42=52
=> 9+16=25 (luôn đúng)
=> đpcm
b) có D nằm trên tia đối của tia AC
=> D,A,C thằng hàng và A nằm giữa D và C
=> DA+AC=DC
=> DA+4=6
=>DA=2(cm)
áp dụng định lý Pytago vào tam giác ABD vuông tại A có:
AB2+AD2=BD2
=> 32+22=BD2
=> 9+4=BD2
=> \(BD=\sqrt{13}\)(cm)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A có AB=6cm,AC=8cm. Kẻ đường cao AH vuông góc với BC (H thuộc BC).
a) Tính độ dài BC.
b) Tia phản giác góc HAC cắt cạnh BC tại D. Qua D kẻ DK vuông góc với AC (K thuộc AC). Chứng minh: tam giác AHD = tam giác AKD.
c) Chứng minh: tam giác BAD cân.
d) Tia phân giác góc BAH cắt cạnh BC tại E. Chứng minh: AB+AC=BC+DE.
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
b) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(cạnh huyền-góc nhọn)
Đúng 4
Bình luận (0)
c) Ta có: ΔADH vuông tại H(gt)
nên \(\widehat{HDA}+\widehat{HAD}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BDA}+\widehat{HAD}=90^0\)(2)
Ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)(tia AD nằm giữa hai tia AB,AC)
nên \(\widehat{BAD}+\widehat{KAD}=90^0\)(3)
Từ (2) và (3) suy ra \(\widehat{BDA}=\widehat{BAD}\)
Xét ΔBAD có \(\widehat{BDA}=\widehat{BAD}\)(cmt)
nên ΔBAD cân tại B(Định lí đảo của tam giác cân)
Đúng 2
Bình luận (1)
Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc với BD cắt BC tại K.
a. Chứng minh: Tam giác ABK cân tại B
b. Chứng minh rằng: DK vuông góc với BC.
c. Kẻ AH vuông góc với BC. Chứng minh rằng: AK là tia phân giác của góc HAC.
d. Gọi I là giao điểm của AH và BD. Chứng minh rằng: IK // AC.
Đọc tiếp
Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc với BD cắt BC tại K.
a. Chứng minh: Tam giác ABK cân tại B
b. Chứng minh rằng: DK vuông góc với BC.
c. Kẻ AH vuông góc với BC. Chứng minh rằng: AK là tia phân giác của góc HAC.
d. Gọi I là giao điểm của AH và BD. Chứng minh rằng: IK // AC.
a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :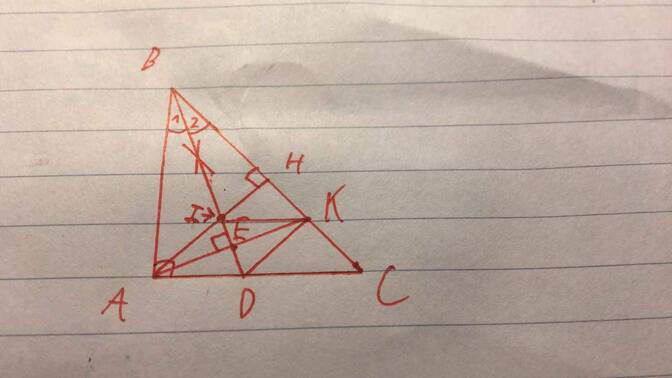
Đúng 3
Bình luận (0)
Cho tam giác ABC cân tại B(B<90độ).Kẻ AH vuông góc với BC(H thuộc BC),CK vuông góc với AB,M là giao điểm của AH và CK
a)Chứng minh AH=CK
b)Chứng minh tam giác ACM cân
c)Trên tia CK lấy điểm D sao cho DK=KC.Chứng minh góc ADC = góc CAH
các bạn giúp mik với mik đang cần gấp lắm,cho mik cảm ơn các bạn trước
a: Xét ΔKAC vuông tại K và ΔHCA vuông tại H có
AC chung
góc KAC=góc HCA
=>ΔKAC=ΔHCA
=>AH=CK
b: Xét ΔMAC có góc MAC=góc MCA
nên ΔMAC cân tại M
c: Xét ΔADC có
AK vừa là đường cao, vừa là trung tuyến
=>ΔADC cân tại A
=>góc ADC=góc ACD
=>góc ADC=góc CAH
Đúng 0
Bình luận (0)