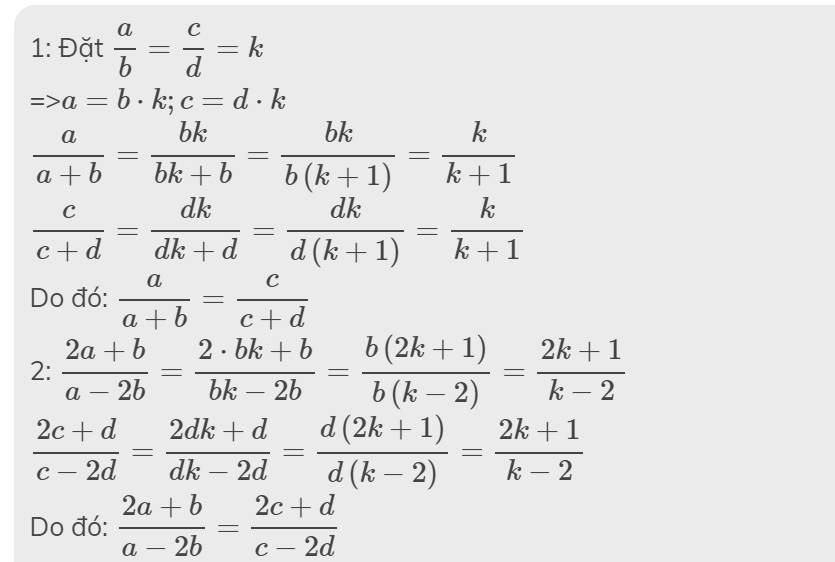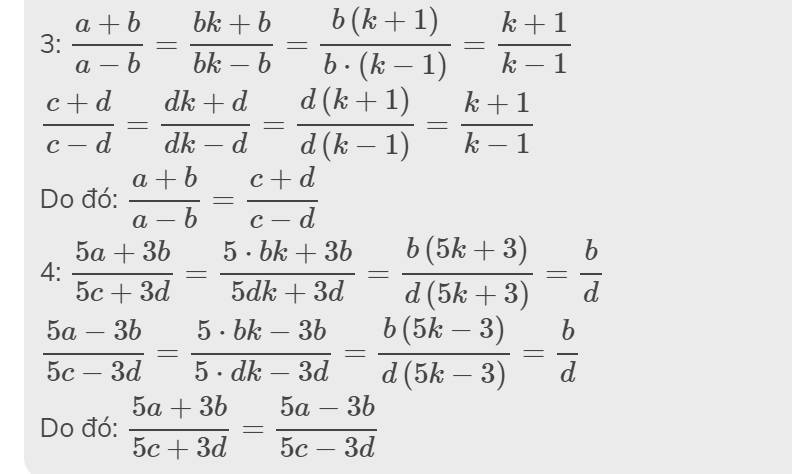5(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)

Những câu hỏi liên quan
Cho tỉ lệ thức a/b = c/d. Chứng yor rằng: a) a/a+b = c/c+d; b) 2.a+b/a-2.b = 2.c+d/c-2.d; c) a+b/a-c = c+d=c-d; d) 5.a+3.b/5.c+3.d = 5.a-3.b/5.c-3.d ( với giả thiết các tỉ số đều có nghĩa)
Cho tỉ lệ thức a/b = c/d. Chứng yor rằng: 1) a/a+b = c/c+d; 2) 2.a+b/a-2.b = 2.c+d/c-2.d; 3) a+b/a-c = c+d=c-d; 4) 5.a+3.b/5.c+3.d = 5.a-3.b/5.c-3.d
1: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(a=b\cdot k;c=d\cdot k\)
\(\dfrac{a}{a+b}=\dfrac{bk}{bk+b}=\dfrac{bk}{b\left(k+1\right)}=\dfrac{k}{k+1}\)
\(\dfrac{c}{c+d}=\dfrac{dk}{dk+d}=\dfrac{dk}{d\left(k+1\right)}=\dfrac{k}{k+1}\)
Do đó: \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
2: \(\dfrac{2a+b}{a-2b}=\dfrac{2\cdot bk+b}{bk-2b}=\dfrac{b\left(2k+1\right)}{b\left(k-2\right)}=\dfrac{2k+1}{k-2}\)
\(\dfrac{2c+d}{c-2d}=\dfrac{2dk+d}{dk-2d}=\dfrac{d\left(2k+1\right)}{d\left(k-2\right)}=\dfrac{2k+1}{k-2}\)
Do đó: \(\dfrac{2a+b}{a-2b}=\dfrac{2c+d}{c-2d}\)
3: \(\dfrac{a+b}{a-b}=\dfrac{bk+b}{bk-b}=\dfrac{b\left(k+1\right)}{b\cdot\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}=\dfrac{d\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)
Do đó: \(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
4: \(\dfrac{5a+3b}{5c+3d}=\dfrac{5\cdot bk+3b}{5dk+3d}=\dfrac{b\left(5k+3\right)}{d\left(5k+3\right)}=\dfrac{b}{d}\)
\(\dfrac{5a-3b}{5c-3d}=\dfrac{5\cdot bk-3b}{5\cdot dk-3d}=\dfrac{b\left(5k-3\right)}{d\left(5k-3\right)}=\dfrac{b}{d}\)
Do đó: \(\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\)
Đúng 3
Bình luận (0)
5 A. B. C. D.6 A. B. C. D.7 A. B. C. D.8 A. B. C. D.9 A. B. C. D.
Đọc tiếp
5

A.

B.

C.

D.

6

A.

B.

C.

D.

7

A.

B.

C.

D.

8

A.

B.

C.

D.

9

A.

B.

C.

D.

1. Cho tỉ lệ thức a/b=c/d chứng minh rằng
a. 2006*(a+c)/2006*a=b+d/b
b.a-b/a+b=c-d/c+d
c.2*a+5*b/3*a-4*b=2*c+5*d/3*c-4*d
d. (a+b/c+d)^3=a^3-b^3/c^3-d^3
1/(a-b+c)-(a+c)=-b
2/(a+b)-(b+a)+c=2a+c
3/-(a+b-c)+(a-b-c)=-2b
4/a(b+c)-a(b+d)=a(c-d)
5/a(b-c)+a(d+c)=a(b+d)
6/a(b-c)-a(b+d)=-a(c+d)
7/(a+b)(c+d)-(a+d)(b+c)=(a-c)(d-b)
1/(a-b+c)-(a+c)=-b
=a-b+c-a-c
=a-a+c-c-b
=0+0-b
=-b
CHỨNG TỎ:
1) (a-b+c)-(a+c)=-b
2) (a+b)-(b-a)+c=2a+c
3)-(a+b-c)+(a-b-c)=-2b
4) a (b+c)-a (b+d)=a (c-d)
5) a (b-c)+a(d+c)=a (b+d)
Xem chi tiết
\(\text{ (a-b+c)-(a+c)}=a-b+c-a-c=\left(a-a\right)-b+\left(c-c\right)=-b\)
\(\left(a+b\right)-\left(b-a\right)+c=a+b-b+a+c=2a+c\)
\(-\left(a+b-c\right)+\left(a-b-c\right)=-a-b+c+a-b-c=-2b\)
\(a\left(b+c\right)-a\left(b+d\right)=ab+ac-ab+ad=ac+ad=a\left(c+d\right)\)
\(a\left(b-c\right)+a\left(d+c\right)=a\left(b-c+d+c\right)=a\left(b+d\right)\)
Đúng 3
Bình luận (1)
a) Tính a , b , c ,d biết a , b , c , d TL vs 2 , 5 , 7 , 6 và a + b + c + d = 7820
b) Tính a , b , c ,d biết a , b , c , d TLN vs 2 , 5 , 7 , 6 và a + b + c + d = 7820
a) a,b,c,d tỉ lệ với 2,5,7,6
\(\Rightarrow\frac{a}{2}=\frac{b}{5}=\frac{c}{7}=\frac{d}{6}\). Áp dụng tính chất dãy tỉ bằng nhau
\(\frac{a}{2}=\frac{b}{5}=\frac{c}{7}=\frac{d}{6}=\frac{a+b+c+d}{2+5+7+6}=\frac{7820}{20}=391\)
Với \(\frac{a}{2}=391\Rightarrow a=782\)Với \(\frac{b}{5}=391\Rightarrow b=1955\)Với \(\frac{c}{7}=391\Rightarrow c=2737\)Với \(\frac{d}{6}=391\Rightarrow d=2346\)
Đúng 0
Bình luận (0)
a) Tính a , b , c ,d biết a , b , c , d TL vs 2 , 5 , 7 , 6 và a + b + c + d = 7820
b) Tính a , b , c ,d biết a , b , c , d TLN vs 2 , 5 , 7 , 6 và a + b + c + d = 7820
1. Tìm 4 số a,b,c,d biết rằng:
a. b + c+ d = 1 ; a + c + d = 2 ; a + b + d = 3 ; a + b + c =4
b. a + b + c + d = 1 ; a + c + d = 5 ; a + b + d = 3 ; a + b + c = 6
a. Ta có :
(b + c + d)+(a + c + d)+(a + b + d)+(a + b + c) = 3(a + b + c + d)
⇒3(a + b + c + d)=1+2+3+4=10
⇒a + b + c + d = \(\dfrac{10}{3}\)
⇒a = (a + b + c + d) - (b + c + d) =\(\dfrac{10}{3}\) - 1= \(\dfrac{7}{3}\)
Tương tự ,ta có :
b = \(\dfrac{10}{3}\) - 2= \(\dfrac{4}{3}\) ; c = \(\dfrac{10}{3}\) - 3= \(\dfrac{1}{3}\)
và d = \(\dfrac{10}{3}\) - 4= \(-\dfrac{2}{3}\)
Vậy các số a,b,c,d lần lượt là \(\dfrac{7}{3}\) ;\(\dfrac{4}{3}\) ;\(\dfrac{1}{3}\) và \(-\dfrac{2}{3}\)
Ý b) tương tự như trên.
Đúng 0
Bình luận (2)
1. a+b/b=c+d/d
2. a-b/b=c-d/d
3. a+b/b=c+d/d
4. a-b/a=c-d/c
5. a/a+b=c/c+d
6. a/a-b=c/c-d
Mong mọi người làm hộ mk ạ thank nhiu