Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB=a, AD=a căn2, SA=a và SA vuông góc với mp đáy. Gọi M là trung điểm của AD và I là giao của BM và AC. Chứng minh (SAC) vuông góc (SMB)
Những câu hỏi liên quan
Cho hình chóp S.ABCD, ABCD là hình chữ nhật. AB=a AD = a căn 3, SA =a. SA vuông góc với đáy. M,N lần lượt là trung điểm AD và SC. BM giao AC tại I
a) CM (SAC) vuông (SMB)
b) tính khoáng cách SB và CD. Tính diện tích tam giác NID
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật,
A
B
S
A
a
,
A
D
a
2
,
S
A
vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AD và SC, gọi I là giao điểm của BM và AC. Tỷ số
V
A
M
N
I
V...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật, A B = S A = a , A D = a 2 , S A vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AD và SC, gọi I là giao điểm của BM và AC. Tỷ số V A M N I V S . A B C D là?
A. 1/24
B. 1/12
C. 1/6
D.1/7
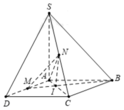
Đáp án A
Vì A M / / B C ⇒ I M I B = M A B C = 1 2 ⇒ d I ; A D d B ; A D = 1 3
|
Suy ra S Δ I M A = 1 2 d I ; A D . A M = 1 2 . 1 3 d B ; A D . 1 2 A D = S A B C D 12
Mà N là trung điểm của S C ⇒ d N ; A B C D = 1 2 d S ; A B C D
Vậy V A M N I V S . A B C D = d N ; A B C D d S ; A B C D . S Δ I M A S A B C D = 1 2 . 1 12 = 1 24
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật, AB SA a, AD a
2
, SA vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AD và SC, gọi I là giao điểm của BM và AC. Tỷ số
V
A
M
N
I
V
S
.
A...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật, AB =SA = a, AD =a 2 , SA vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AD và SC, gọi I là giao điểm của BM và AC. Tỷ số V A M N I V S . A B C D là ?
A. 1 7
B. 1 12
C. 1 6
D. 1 24
Đáp án là D
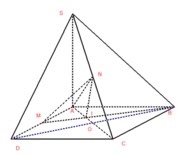
Coi hình chóp AMNI với điểm N làm đỉnh và AMI làm đáy
+) Từ N là trung điểm của SC nên đường cao
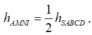
+) Lấy O là tâm hình chữ nhật ta có BM, AO là các trung tuyến nên I là trọng tâm tam giác ABD nên
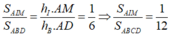
+) Suy ra
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật, AB SA a, AD a
2
, SA vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AD và SC, gọi I là giao điểm của BM và AC. Tỷ số
V
A
M
N
I
V
S
A
B
C
D...
Đọc tiếp
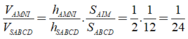
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật, AB =SA = a, AD =a 2 , SA vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AD và SC, gọi I là giao điểm của BM và AC. Tỷ số V A M N I V S A B C D là ?
A. 1 7
B. 1 12
C. 1 6
D. 1 24
Cho hình chóp S.ABCD có đáy là hình chữ nhật,
A
B
a
2
,
A
D
a
và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của đoạn thẳng AB. Góc giữa hai mặt phẳng (SAC) và (SDM) bằng A. 30
°
B. 45
°
C. 60
°
D. 90
°
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật, A B = a 2 , A D = a và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của đoạn thẳng AB. Góc giữa hai mặt phẳng (SAC) và (SDM) bằng
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB
2
a
, AD2a, SA vuông góc với đáy và SA
2
a
Gọi M và N lần lượt là trung điểm của SB và AD( tham khảo hình vẽ). Côsin góc giữa đường thẳng MN và mặt phẳng (SAC) bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB= 2 a , AD=2a, SA vuông góc với đáy và SA= 2 a Gọi M và N lần lượt là trung điểm của SB và AD( tham khảo hình vẽ). Côsin góc giữa đường thẳng MN và mặt phẳng (SAC) bằng
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B,
A
B
B
C
a
,
A
D
2
a
,
S
A
vuông góc với mặt đáy
A
B
C
D
,
S
A
a
. Gọi M, N lần lượt là trung điểm của SB, CD. Tính cosin của góc gi...
Đọc tiếp
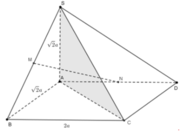
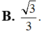
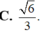
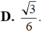
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, A B = B C = a , A D = 2 a , S A vuông góc với mặt đáy A B C D , S A = a . Gọi M, N lần lượt là trung điểm của SB, CD. Tính cosin của góc giữa MN và (SAC).
A. 2 5
B. 55 10
C. 3 5 10
D. 1 5
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD. a) Cmr: CD vuông góc mp (SAD) b) Cmr: (SAC) vuông góc mp (SBD) c) Tính góc giữa SC v à mp (ABCD) d) Tính góc giữa mp ( SAB) và mp (SBC). e) Tính khoảng cách từ A đến mp ( SBD)
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB=a; AD= 2a; SA vuông góc với đáy, SA=a√2. Xác định và tính góc giữa. a) Các đường thẳng SB, SC, SD với mp đáy. b) SC với các mp (SAD) và ( SAB). c) SA với mp (SCD). d) SB và (SAC).
