có tác dụng chú thích nha bạn

Cái này em chịu tại em lớp 3 cơ

cảm ơn Ninh nhé 

Mình đg rất cần gấp giúp mình nhé 

9.

\(\Leftrightarrow a^2+a^2b^2+b^2+b^2c^2+c^2+c^2a^2\ge6abc\)

\(\Leftrightarrow\left(a^2-2abc+b^2c^2\right)+\left(b^2-2abc+c^2a^2\right)+\left(c^2-2abc+a^2b^2\right)\ge0\)

\(\Leftrightarrow\left(a-bc\right)^2+\left(b-ca\right)^2+\left(c-ab\right)^2\ge0\) (luôn đúng)

Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(0;0;0\right);\left(1;1;1\right);\left(1;-1;-1\right)\) và các hoán vị

10.

\(a^2+b^2+c^2=1\)

\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=1+2\left(ab+bc+ca\right)\)

\(\Leftrightarrow\left(a+b+c\right)^2=1+2\left(ab+bc+ca\right)\)

\(\Rightarrow1+2\left(ab+bc+ca\right)\ge0\Rightarrow ab+bc+ca\ge-\dfrac{1}{2}\)

Lại có:

\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)

\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)

\(\Rightarrow ab+bc+ca\le1\)

11.

Do \(a^2+b^2+c^2=1\Rightarrow\left\{{}\begin{matrix}\left|a\right|\le1\\\left|b\right|\le1\\\left|c\right|\le1\end{matrix}\right.\) \(\Rightarrow\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge0\)

Do đó:

\(abc+2\left(1+a+b+c+ab+bc+ca\right)\)

\(=1+a+b+c+ab+bc+ca+\left(1+a+b+c+ab+bc+ca+abc\right)\)

\(=\dfrac{1}{2}\left(a^2+b^2+c^2\right)+ab+bc+ca+a+b+c+\dfrac{1}{2}+\left(a+1\right)\left(b+1\right)\left(c+1\right)\)

\(=\dfrac{1}{2}\left(a+b+c\right)^2+\left(a+b+c\right)+\dfrac{1}{2}+\left(a+1\right)\left(b+1\right)\left(c+1\right)\)

\(=\dfrac{1}{2}\left(a+b+c+1\right)^2+\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge0\) (đpcm)

12.

\(a^4+3\ge4a\)

\(\Leftrightarrow a^4-2a^3+a^2+\left(2a^3-4a^2+2a\right)+\left(3a^2-6a+3\right)\ge0\)

\(\Leftrightarrow a^2\left(a-1\right)^2+2a\left(a-1\right)^2+3\left(a-1\right)^2\ge0\)

\(\Leftrightarrow\left(a^2+2a+3\right)\left(a-1\right)^2\ge0\)

\(\Leftrightarrow\left[\left(a+1\right)^2+2\right]\left(a-1\right)^2\ge0\) (luôn đúng)

a) \(x^2-2\left(m-4\right)x-2m+3=0\)

\(\Delta'=[-\left(m-4\right)]^2-\left(-2m+3\right)\)

\(\Delta'=m^2-8m+16+2m-3\)

\(\Delta'=m^2-6m+13\)

\(\Delta'=\left(m-3\right)^2+4>0\)( với mọi m)

Vậy phương trình(1) luôn có 2 nghiệm phân biệt với mọi m

b)Để phương trình có 2 nghiệm phân biệt cùng âm 

Thì \(-2m+3>0\)

⇔\(-2m>-3\)

⇔\(m< \dfrac{3}{2}\)

c,Vì phương trình (1) có nghiệm 

Nên theo định lí Vi-et ta có

\(x_1+x_2=2\left(m-4\right)\)

\(x_1\cdot x_2=-2m+3\)

Ta có \(x_1+x_2=2\left(m-4\right)\)

⇔\(x_1+x_2+8=2m\)

⇔\(m=\dfrac{x_1+x_2+8}{2}\)(2)

Ta có \(x_1\cdot x_2=-2m+3\)

⇔\(x_1\cdot x_2-3=-2m\)

⇔\(m=-\dfrac{x_1\cdot x_2-3}{2}\)(3)

Từ (2) và(3)

⇒\(\dfrac{x_1+x_2+8}{2}\)=\(-\dfrac{x_1\cdot x_2-3}{2}\)

mình làm trước 3 câu trên .Còn câu cuối do có việc bận nên mình bỏ qua nha

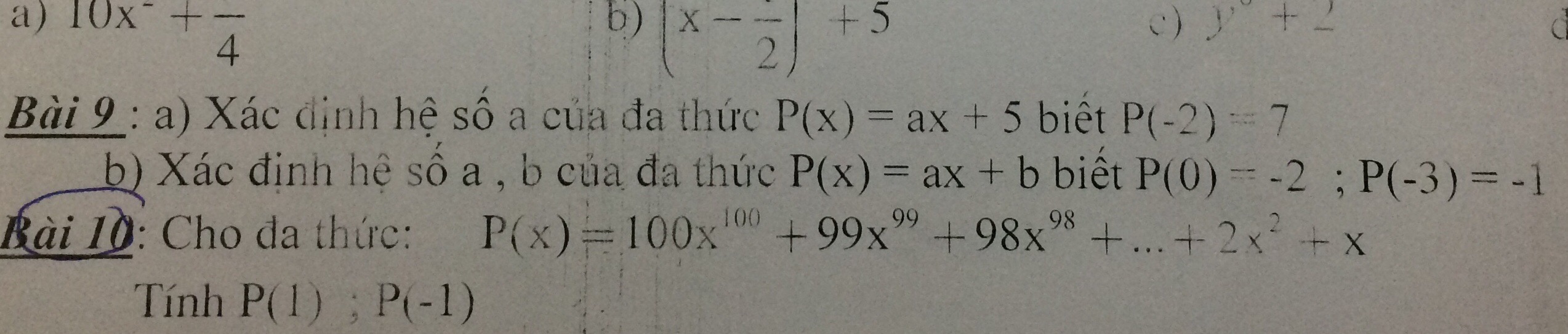
9a.

Do \(P\left(-2\right)=7\)

\(\Rightarrow a.\left(-2\right)+5=7\)

\(\Rightarrow-2a=2\)

\(\Rightarrow a=-1\)

b.

Do \(P\left(0\right)=-2\)

\(\Rightarrow a.0+b=-2\)

\(\Rightarrow b=-2\)

Do \(P\left(-3\right)=-1\)

\(\Rightarrow a.\left(-3\right)+b=-1\)

\(\Rightarrow-3a-2=-1\)

\(\Rightarrow-3a=1\)

\(\Rightarrow a=-\dfrac{1}{3}\)

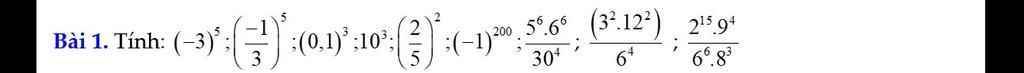
Lời giải:

$(-3)^5 = -243$

$(\frac{-1}{3})^5=\frac{(-1)^5}{3^5}=\frac{-1}{243}$

$(0,1)^3=0,001$
$10^3=1000$

$(\frac{2}{5})^2=\frac{2^2}{5^2}=\frac{4}{25}=0,16$

$(-1)^{200}=1$

$\frac{5^6.6^6}{30^4}=\frac{(5.6)^6}{30^4}=\frac{30^6}{30^4}=30^2=900$

$\frac{3^2.12^2}{6^4}=\frac{3^2.2^2.6^2}{6^4}=\frac{(3.2)^2.6^2}{6^4}$

$=\frac{6^2.6^2}{6^4}=\frac{6^4}{6^4}=1$

$\frac{2^{15}.9^4}{6^6.8^3}=\frac{2^{15}.(3^2)^4}{2^6.3^6.(2^3)^3}$

$=\frac{2^{15}.3^{8}}{2^6.3^6.2^9}=\frac{2^{15}.3^8}{2^{15}.3^6}=\frac{3^8}{3^6}=3^2=9$

8a.

\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(3x^2-5x+1\right)=3-5+1=-1\)

\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(-3x+2\right)=-3+2=-1\)

\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Rightarrow\) hàm có giới hạn tại \(x=1\)

Đồng thời \(\lim\limits_{x\rightarrow1}f\left(x\right)=-1\)

b.

\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{x-2}=\lim\limits_{x\rightarrow2^+}\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}\)

\(=\lim\limits_{x\rightarrow2^+}\left(x^2+2x+4\right)=12\)

\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(2x+1\right)=5\)

\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\Rightarrow\) hàm ko có giới hạn tại x=2

9.

\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{x^2+mx+2m+1}{x+1}=\dfrac{0+0+2m+1}{0+1}=2m+1\)

\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2x+3m-1}{\sqrt{1-x}+2}=\dfrac{0+3m-1}{1+2}=\dfrac{3m-1}{3}\)

Hàm có giới hạn khi \(x\rightarrow0\) khi:

\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\Rightarrow2m+1=\dfrac{3m-1}{3}\)

\(\Rightarrow m=-\dfrac{4}{3}\)