Gọi độ dài 1 cạnh góc vuông là x (cm), x < 25

độ dài cạnh góc vuông còn lại là 60 - 25 - x = 35 - x (cm)

Theo đề bài ta có pt :

x + (35 - x ) = 25^2 (ĐL Pytago) <=> x^2 - 35x + 300 = 0 

Δ = (−35)² − 4.1.300 = 25 

x = (35+5) : 2 = 20 ; x = 35 - 20 = 15

Vậy độ dài 2 góc vuông là 20cm và 15cm

Gọi độ dài 1 cạnh góc vuông là x (cm), x < 25

       độ dài cạnh góc vuông còn lại là 60 - 25 - x = 35 - x (cm)

Theo đề bài ta có pt :

x² + (35 - x²) = 25^2 (ĐL Pytago) <=> x^2 - 35x + 300 = 0

\(\Delta=\left(-35\right)^2-4.1.300=25\)

x₁ = (35+5) : 2 = 20 ; x₂ = 35 - 20 = 15

Vậy độ dài 2 góc vuông là 20cm và 15cm

2 bạn đều copy mạng

Gọi x là dộ dài cạnh góc vuông thứ nhất (x < 20)

=> độ dài cạnh góc vuông thứ hai : 48 - 20 -x =28 - x

Theo đề bài ta có pt:

x² + (28 -x)² =20² (giải pt tìm x)

Gọi độ dài đoạn thẳng ngắn hơn được chia trên cạnh huyền là x (cm) với x>0

\(\Rightarrow\) Độ dài đoạn còn lại là \(x+14\)

Áp dụng hệ thức lượng trong tam giác vuông:

\(24^2=x\left(x+14\right)\)

\(\Leftrightarrow x^2+14x-576=0\Rightarrow\left[{}\begin{matrix}x=18\\x=-32\left(loại\right)\end{matrix}\right.\)

\(\Rightarrow\) Độ dài cạnh huyền là: \(18+\left(18+14\right)=50\left(cm\right)\)

Diện tích tam giác: \(S=\dfrac{1}{2}.24.50=600\left(cm^2\right)\)

Gọi độ dài các cạnh góc vuông của tam giác lần lượt là 5k và 12k với k> 0. Dùng định lý Py-ta-go tính được độ dài cạnh huyền là 13k, do đó

5k +12k + 13k = 30 => k = 1.

Từ đó độ dài cạnh huyền là 13 cm.

Gọi b, c là độ dài các cạnh góc vuông, a là độ dài cạnh huyền (tính bằng cm) ( 0 < b; c < a)

+) Do các cạnh góc vuông tỉ lệ với 7 và 24 nên:

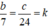 ⇒ b = 7k, c = 24k.

Theo định lý Py-ta-go:

a2 = b2 + c2 = (7k)2 + (24k)2 = 625k2 = (25k)2

Nên a = 25k.

Theo đề bài, chu vi tam giác bằng 112 cm nên: a + b + c = 112 (cm).

Suy ra: 25k + 7k + 24k = 112

Hay 56k = 112

Từ đó ta tính được k = 2. Vậy a = 50cm.

Lời giải:
Gọi độ dài cạnh góc vuông lần lượt là $a$ và $b$ ($a>b>0$) (cm) 

Áp dụng định lý Pitago: $a^2+b^2=60^2=3600(*)$ 

$a-b=12$

$\Leftrightarrow a=b+12$. Thay vào $(*)$ thì:

$(b+12)^2+b^2=3600$

$\Leftrightarrow 2b^2+24b-3456=0$

$\Leftrightarrow b^2+12b-1728=0$

$\Leftrightarrow (b-36)(b+48)=0$

Do $b>0$ nên $b=36$ (cm)

$a=b+12=36+12=48$ (cm)