Với mỗi lần cắt hoặc gấp, hãy tạo ra hình thang cân từ:
a) Mảnh bìa có dạng hình tam giác đều;
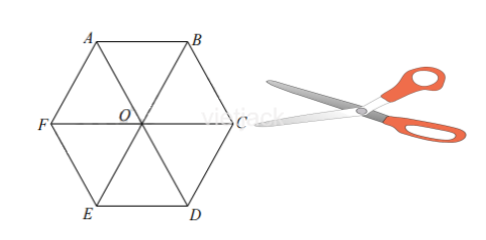
b) Mảnh bìa có dạng hình lục giác đều.
Với một lần cắt hoặc gấp, hãy tạo ra hình thanh cân từ:
a) Mảnh bìa có dạng hình tam giác đều,
b) Mảnh bìa có dạng hình lục giác đều.
tham khảo :
a) Ta cắt hoặc gấp mảnh bìa hình tam giác đều theo một đường thẳng đi qua hai cạnh và song song với cạnh còn lại của hình tam giác đó, ta được hình thang cân.

b) Ta cắt hoặc gấp mảnh bìa hình lục giác đều theo một đường chéo chính FC (hoặc AD hoặc BE) ta được hình thang cân.
Cắt một tấm bìa hình tam giác cân, một tấm bìa hình thang cân. Hãy cho biết đường nào là trục đối xứng của mỗi hình, sau đó gấp mỗi tấm bìa để kiểm tra lại điều đó.
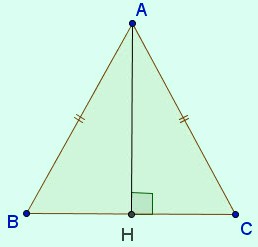
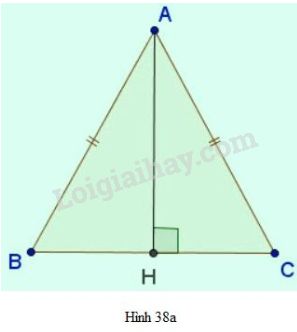
- ΔABC cân tại A có trục đối xứng là đường phân giác AH của góc BAC (đường này đồng thời là đường cao, đường trung trực, đường trung tuyến).
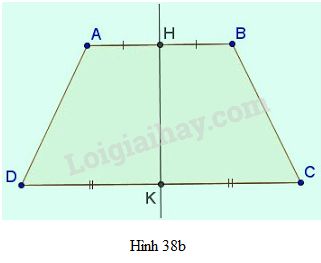
– Hình thang cân ABCD nhận đường thẳng đi qua trung điểm hai đáy HK làm trục đối xứng.
Thực hành. Cắt một tấm bìa hình tam giác cân, một tấm bìa hình thang cân. Hãy cho biết đường nào là trục đối xứng của mỗi hình, sau đó gấp mỗi tấm bìa để kiểm tra lại điều đó.
1 . CHO MỘT MẢNH BÌA HÌNH TAM GIÁC .HÃY CẮT MẢNH BÌA ĐÓ THÀNH 2 MẢNH BÌA HÌNH TAM GIÁC SAO CHO DIỆN TÍCH MẢNH NÀY GẤP 3 LẦN MẢNH KIA
Thực hành. Cắt một tấm bìa hình tam giác cân, một tấm bìa hình thang cân. Hãy cho biết đường nào là trục đối xứng của mỗi hình, sau đó gấp mỗi tấm bìa để kiểm tra lại điều đó.
Thực hành :
Cắt một tấm bìa hình tam giác cân, một tấm bìa hình thang cân. Hãy cho biết đường nào là trục đối xứng của mỗi hình, sau đó gấp mỗi tấm bìa để kiểm tra lại điều đó ?
Chú ý:
- ∆ABC cân tại A có trục đối xứng là đường phân giác của góc BAC.
- Hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng.
Đối với tam giác cân hình 38a:
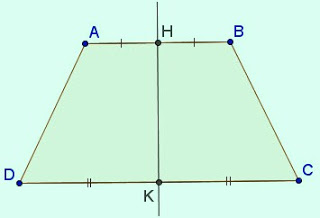 Hình thang cân ABCD (AB // CD), trục đối xứng là đường thẳng KH với K, H lần lượt là trung điểm của AB và CD.
Hình thang cân ABCD (AB // CD), trục đối xứng là đường thẳng KH với K, H lần lượt là trung điểm của AB và CD.
Đối với tam giác cân hình 38a:
Tạo lập hình chóp tam giác đều có độ dài cạnh đáy 3cm và cạnh bên 4cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình tam giác đều và ba hình tam giác cân với kích thước như Hình 7a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tam giác đều như Hình 7b.
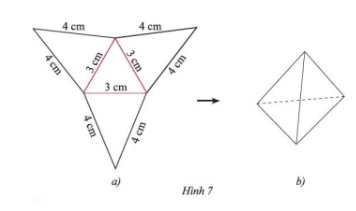
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như hình 7b.
Vẽ, cắt và gấp miếng bìa như hình đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.
a) Trong hình 125a, có bao nhiêu tam giác cân bằng nhau?
b) Sử dụng định lí Pitago để tính chiều cao ứng với đáy của mỗi tam giác.
c) Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu?
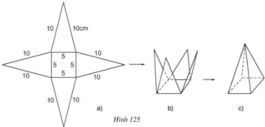
a) Trong hình 125a có 4 tam giác cân bằng nhau.
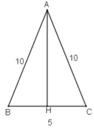
b) Gọi H là trung điểm BC. Tam giác ABC có AH là đường trung tuyến nên đồng thời là đường cao.
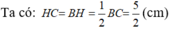
Chiều cao ứng với đáy của mỗi tam giác:
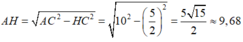
c) Chu vi đáy của hình chóp là 4.5 = 20 (cm).
Diện tích xung quanh hình chóp:
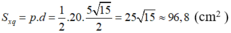
Diện tích đáy: Sd = 52 = 25 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sd + Sxq = 121,8 (cm2)
Vẽ, cắt và gấp miếng bìa như hình đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.
a) Trong hình 125a, có bao nhiêu tam giác cân bằng nhau?
b) Sử dụng định lí Pitago để tính chiều cao ứng với đáy của mỗi tam giác.
c) Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu?
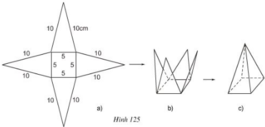
a) Trong hình 125a có 4 tam giác cân bằng nhau.
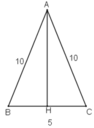
b) Gọi H là trung điểm BC. Tam giác ABC có AH là đường trung tuyến nên đồng thời là đường cao.
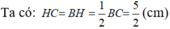
Chiều cao ứng với đáy của mỗi tam giác:
c) Chu vi đáy của hình chóp là 4.5 = 20 (cm).
Diện tích xung quanh hình chóp:
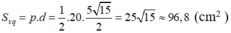
Diện tích đáy: Sd = 52 = 25 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sd + Sxq = 121,8 (cm2)