2005 se có tận cùng là 5

Vì các số 2 mũ luôn có số tận cùng lần lượt là 2;4;6;8

ta có:

2005:4=501 dư 1 suy ra tận cùng là chữ số 2 : 5+2=7

Vì 2005 không chia hết cho 3 hay 9

Mà các số tận cùng là 7 và 5

suy ra 2 số trên là 2 số nguyên tố cùng nhau

mày lấy vì 2006^2005 +và -1 >3

xét 3 số tự nhiên liên tiếp luôn có 1 số chia hết cho 3 

vì 2006 không chia hết cho 3, 3 là số nguyên tố 

2006^2005 không chia hết cho 3

2006^2005-1 hoặc 2006^2005+1 chia hết co 3 

tự tiếp k nha

chưa làm được

ra rồi hoài ơi

Hằng đẳng thức a² - b² = (a - b).(a + b) <=> (a - b).(a + b) = a² - b²

bạn nên hỏi luôn khi cô giảng chứ, đừng giấu dốt nhé

(Ghi chú: Muốn chứng minh hai số là nghịch đảo của nhau, ta chứng minh tích của hai số bằng 1.)

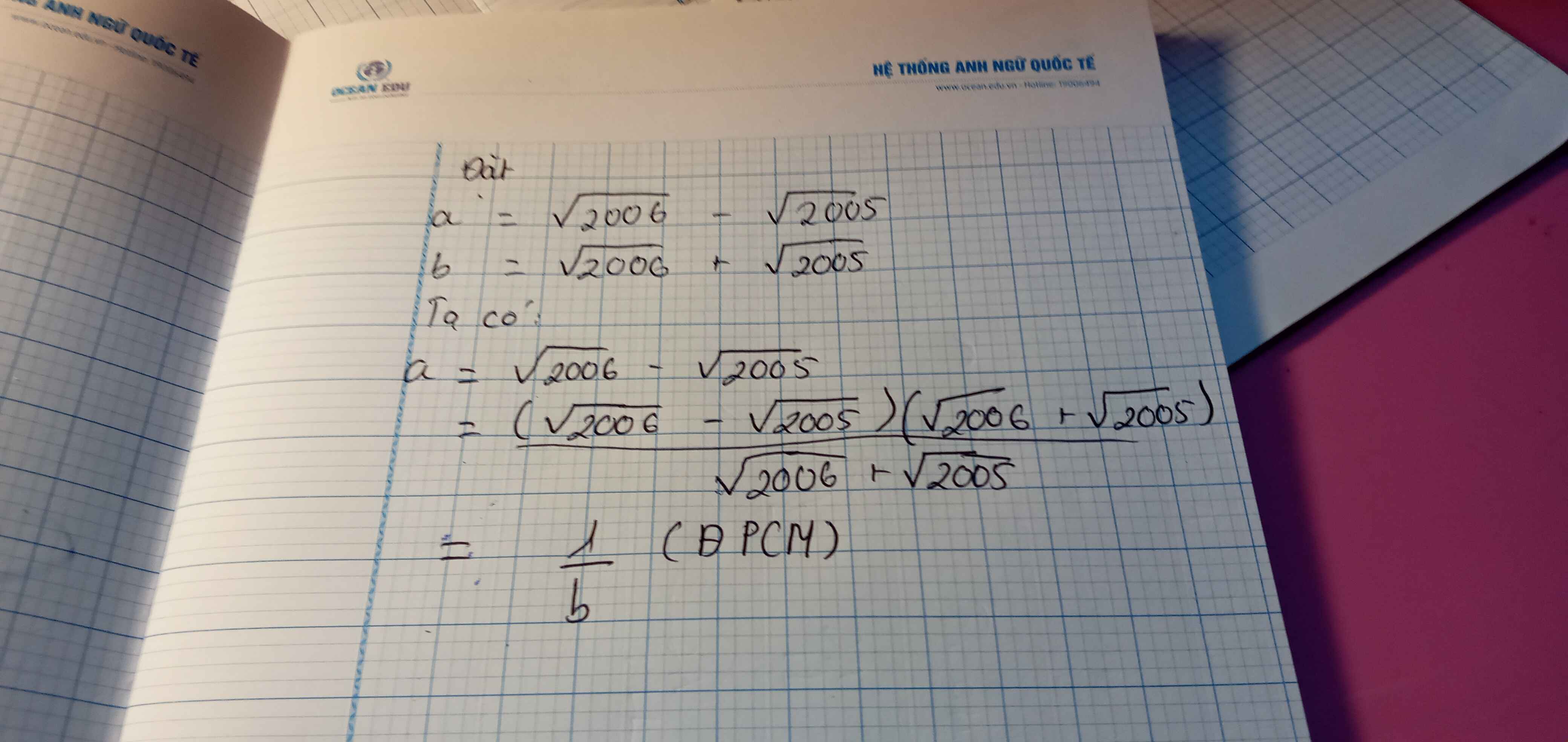
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)

Ta có 

\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)

\(\RightarrowĐfcm\)

\(\sqrt{2006}-\sqrt{2005}=\dfrac{1}{\sqrt{2006}+\sqrt{2005}}\)

Do đó: \(\sqrt{2006}-\sqrt{2005};\sqrt{2006}+\sqrt{2005}\) là hai số nghịch đảo