S.o.S, ai giải hộ mk câu 10 với ạ

Những câu hỏi liên quan

 Ai giải hộ mik với, ý b và câu 10 ạ
Ai giải hộ mik với, ý b và câu 10 ạ
Câu 10 của em đây nhé:
\(\dfrac{17}{2}\) \(\times\) \(\dfrac{3}{5}\) + \(\dfrac{3}{5}\) \(\times\) \(\dfrac{1}{2}\) + \(\dfrac{3}{5}\)
= \(\dfrac{17}{2}\) \(\times\) \(\dfrac{3}{5}\) + \(\dfrac{3}{5}\) \(\times\) \(\dfrac{1}{2}\) + \(\dfrac{3}{5}\) \(\times\) 1
= \(\dfrac{3}{5}\) \(\times\) ( \(\dfrac{17}{2}\) + \(\dfrac{1}{2}\) + 1)
= \(\dfrac{3}{5}\) \(\times\) ( \(\dfrac{18}{2}\) + 1)
= \(\dfrac{3}{5}\) \(\times\) ( 9 + 1)
= \(\dfrac{3}{5}\) \(\times\) 10
= 6
Đúng 3
Bình luận (0)
Bước 1 em rút gọn phân số.
Bước 2 em thực hiện theo quy tắc thực hiện phép tính
Bước 3 em tính bằng cách hợp lý
ý b của em đây nhé:
\(\dfrac{2018}{2010}\) - \(\dfrac{2}{49}\) : \(\dfrac{3}{21}\) + \(\dfrac{12}{24}\) \(\times\) \(\dfrac{4}{7}\)
= \(\dfrac{1009}{1005}\) - \(\dfrac{2}{49}\) : \(\dfrac{1}{7}\) + \(\dfrac{1}{2}\) \(\times\) \(\dfrac{4}{7}\)
= \(\dfrac{1009}{1005}\) - \(\dfrac{2}{49}\) \(\times\) \(\dfrac{7}{1}\) + \(\dfrac{2}{7}\)
= \(\dfrac{1009}{1005}\) - \(\dfrac{2}{7}\) + \(\dfrac{2}{7}\)
= \(\dfrac{1009}{1005}\) - ( \(\dfrac{2}{7}\) - \(\dfrac{2}{7}\))
= \(\dfrac{1009}{1005}\) - 0
= \(\dfrac{1009}{1005}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Ai giải hộ mình câu 10 và 11 với! Mik cảm ơn nhiều ạ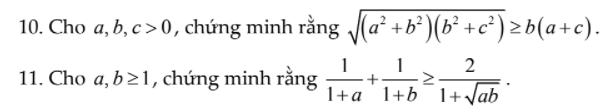 !
!
10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
Đúng 1
Bình luận (0)
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)
Đúng 0
Bình luận (0)
Ai giải hộ mình câu 10 và 11 với! Mik cảm ơn rất nhiều ạ.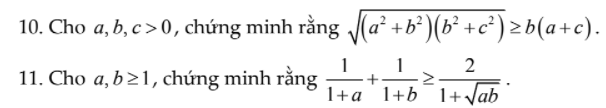
dùng phương pháp hình học cm câu a
đặt BH =a , HC =c kẻ HA =b
theo định lí py ta go ta có
AB=a2+b2;AC=b2+c2;BC=a+b
dễ thấy AB.AC\(\ge\) 2SABC=BC.AH
(a2+b2).(b2+c2)\(\ge\)b.(a+c)
Đúng 0
Bình luận (0)
Ai giải hộ mình câu 10 và 11 với! Mik đang cần ạ, cảm ơn nhiều!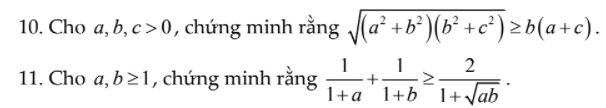
Ai đó giúp mk câu 3 đi ạ, mình đang cần gấp ạ. Giải thích vì sao hộ mình nữa nhé anh please 
Giải hộ mk câu 2,3,4 tự luận với ạ
Mk cảm ơn nhiều 🤗

giải hộ mk câu này với ạ.Mk cảm ơn ạ ^^
ĐKXĐ: ...
Với \(\left[{}\begin{matrix}x=0\\y=0\end{matrix}\right.\) ko phải nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}2-\dfrac{1}{2x+y}=\dfrac{2}{\sqrt{y}}\\2+\dfrac{1}{2x+y}=\dfrac{2}{\sqrt{x}}\end{matrix}\right.\)
Lần lượt cộng vế với vế và trừ vế cho vế 2 pt ta được:
\(\left\{{}\begin{matrix}2=\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}\\\dfrac{1}{2x+y}=\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{y}}\end{matrix}\right.\)
Nhân vế với vế:
\(\dfrac{2}{2x+y}=\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}\right)\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{y}}\right)\)
\(\Leftrightarrow\dfrac{2}{2x+y}=\dfrac{1}{x}-\dfrac{1}{y}\)
\(\Leftrightarrow2x^2+xy-y^2=0\)
\(\Leftrightarrow\left(x+y\right)\left(2x-y\right)=0\)
\(\Leftrightarrow...\)
Đúng 1
Bình luận (1)
Ai giải hộ e câu 8 với ạ
Câu 8 :B
m NaCl = 200.5% = 10(gam)
m H2O = m dd - m NaCl = 200 - 10 = 190(gam)
Đúng 3
Bình luận (0)
Câu 8:
mNaCl=5%.200=10(g)
=>mH2O=mddNaCl - mNaCl= 200-10=190(g)
=> Điều chế: Hòa tan 10 gam NaCl vào 190 gam H2O
=> CHỌN B
Đúng 1
Bình luận (0)
ai giải hộ e 2 câu này với ạ .nhanh giúp e với
















