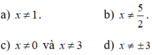Tìm GTLN của biểu thức: M= - 9x2+6x-3>0,\(\forall\)x

Những câu hỏi liên quan
Tìm điều kiện của x để giá trị của biểu thức được xác định:a)
3
x
3
(
x
−
1
)
(
x
2
+
2
)
;
b)
−
4...
Đọc tiếp
Tìm điều kiện của x để giá trị của biểu thức được xác định:
a) 3 x 3 ( x − 1 ) ( x 2 + 2 ) ; b) − 4 x 2 25 − 20 x + 4 x 2 ;
c) x 2 − 9 x 2 − 6 x + 9 2 x ; d) x 2 − 9 x 2 + 6 x + 9 x − 3 .
tìm gtln của biểu thức √x-1 + √16-6x +√6x-3
tìm gtln của biểu thức: E= -x^4-10x^2-6x^3-6x+15
\(E=-\left(x^4+10x^2+9+6x^3+6x\right)+24\)
\(=-\left[\left(x^2+9\right)\left(x^2+1\right)+6x\left(x^2+1\right)\right]+24\)
\(=-\left(x^2+1\right)\left(x^2+9+6x\right)+24\)
\(=-\left(x^2+1\right)\left(x+3\right)^2+24\le24\)
\(E_{max}=24\) khi \(x=-3\)
Đúng 2
Bình luận (0)
Tìm GTLN của biểu thức :
\(A=x^4-6x^3+9x^2+6x+2021\)
Cho biểu thức: 2(1-9x2)/3x2+6x : 2-6x/3x
a, Rút gọn M.
b, Tìm các giá trị nguyên của x để M có giá trị nguyên.
c.tìm các giá trị nguyên của x =2 ,x=1
các bạn giúp vơi mình đang thi
a: \(M=\dfrac{2\left(1-3x\right)\left(1+3x\right)}{3x\left(x+2\right)}\cdot\dfrac{3x}{2\left(1-3x\right)}=\dfrac{3x+1}{x+2}\)
Đúng 1
Bình luận (1)
Tìm GTNN của biểu thức: 9x2+y2-6x+5
(9x^2-6x+1)+y^2+4
=(3x-1)^2+y^2+4
ta có (3x-1)^2>= 0
=>(3x-1)^2+y^2>=0
=>(3x-1)^2+y^2+4>=4
GTNN biểu thức là 4 và xảy ra khi 3x-1=0=>x=1/3, y=0
Đúng 0
Bình luận (0)
tìm GTNN của biểu thức
2/6x-5-9x2
`2/[6x-5-9x^2]`
`=-2/[9x^2-6x+5]`
`=-2/[(3x-1)^2+4]`
Vì `(3x-1)^2 >= 0 AA x`
`<=>(3x-1)^2+4 >= 4 AA x`
`<=>1/[(3x-1)^2+4] <= 1/4`
`<=>-2/[(3x-1)^2+4] >= -1/2 AA x`
`=>Mi n=-1/2`
Dấu "`=`" xảy ra `<=>3x-1=0<=>x=1/3`
Đúng 2
Bình luận (0)
Tìm GTLN, GTNN của biểu thức: `C=(6x+11)/(x^2-2x+3)`
Bài 6: a)Tìm GTLN, GTNN của biểu thức sau:a. x2 – 6x +11 b. –x2 + 6x – 11 c) Chứng minh rằng: x2 + 2x + 2 0 với x Z
Đọc tiếp
Bài 6: a)Tìm GTLN, GTNN của biểu thức sau:
a. x2 – 6x +11 b. –x2 + 6x – 11
c) Chứng minh rằng: x2 + 2x + 2 > 0 với x Z
c: \(=\left(x+1\right)^2+1>0\forall x\)
Đúng 0
Bình luận (0)
Trả lời:
a, \(x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTNN của biểu thức bằng 2 khi x = 3
b, \(-x^2+6x-11=-\left(x^2-6x+11\right)=-\left(x^2-6x+9+2\right)=-\left[\left(x-3\right)^2+2\right]\)
\(=-\left(x-3\right)^2-2\le-2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTLN của biểu thức bằng - 2 khi x = 3
c, \(x^2+2x+2=x^2+2x+1+1=\left(x+1\right)^2+1\ge1>0\forall x\inℤ\) (đpcm)
Dấu "=" xảy ra khi x + 1 = 0 <=> x = - 1