d ) 45,24 : 1,8
Cíu tui :<
Viết ra giấy đầy đủ cách làm nha mn
Đặt tính rồi tính
a) 54,665 + 174,55 b) 35,2 – 17,855
c) 25,7 x 0,17 d) 45,24 : 1,8

giải câu c d thôi ạ cíu tui cíu tui
Đề bài không rõ ràng, em liên hệ người ra đề xem vẽ đồ thị đường thẳng nào? Vì đường thẳng đề cho có a chưa biết
 cíu tui cíu tui
cíu tui cíu tui
1: Xét ΔMNP vuông tại M có MH là đường cao
nên MH^2=HN*HP; MN^2=NH*NP; PM^2=PH*PN
=>MH=căn 3,6*6,4=4,8cm; MN=căn 3,6*10=6cm; PM=căn 6,4*10=8cm
2: MK=8/2=4cm
Xét ΔMNK vuông tại M có tan MNK=MK/MN=4/6=2/3
nên \(\widehat{MNK}\simeq33^041'\)
3: ΔMNK vuông tại M có MF là đường cao
nên NF*NK=NM^2
ΔMNP vuông tại M có MH là đường cao
nên NH*NP=NM^2
=>NF*NK=NH*NP
cíu tui cíu tui ![]()
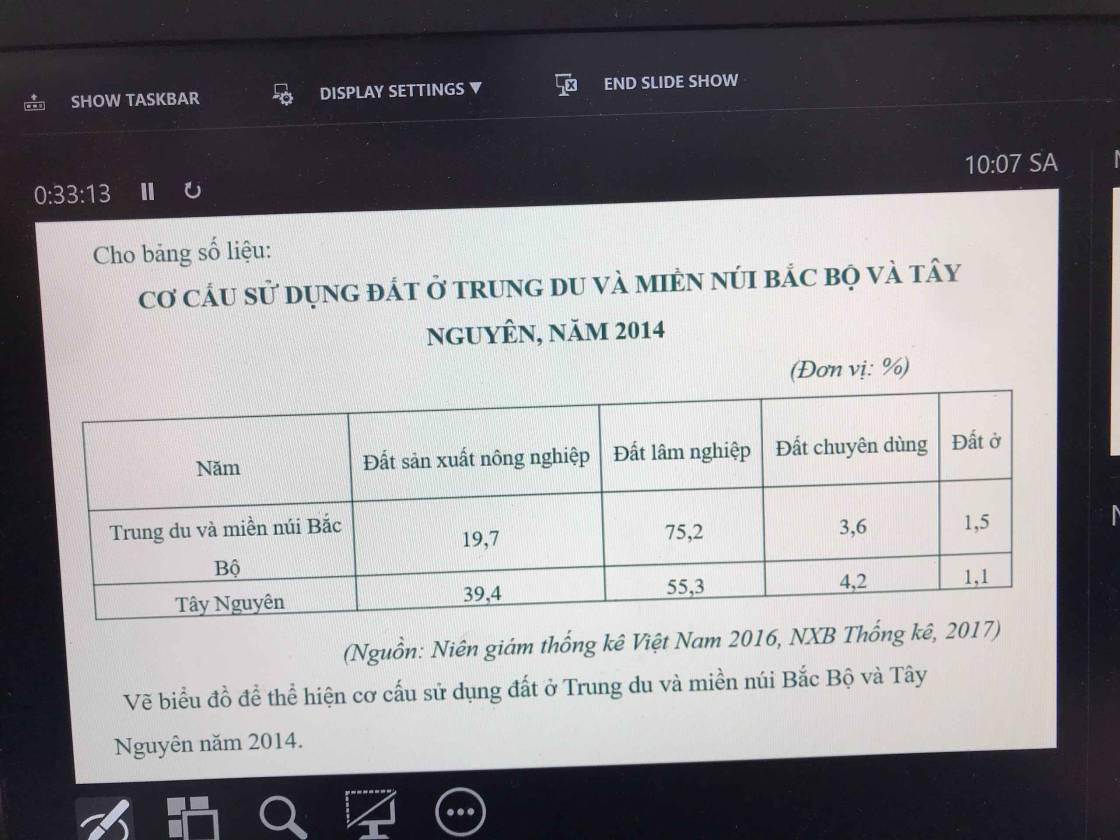

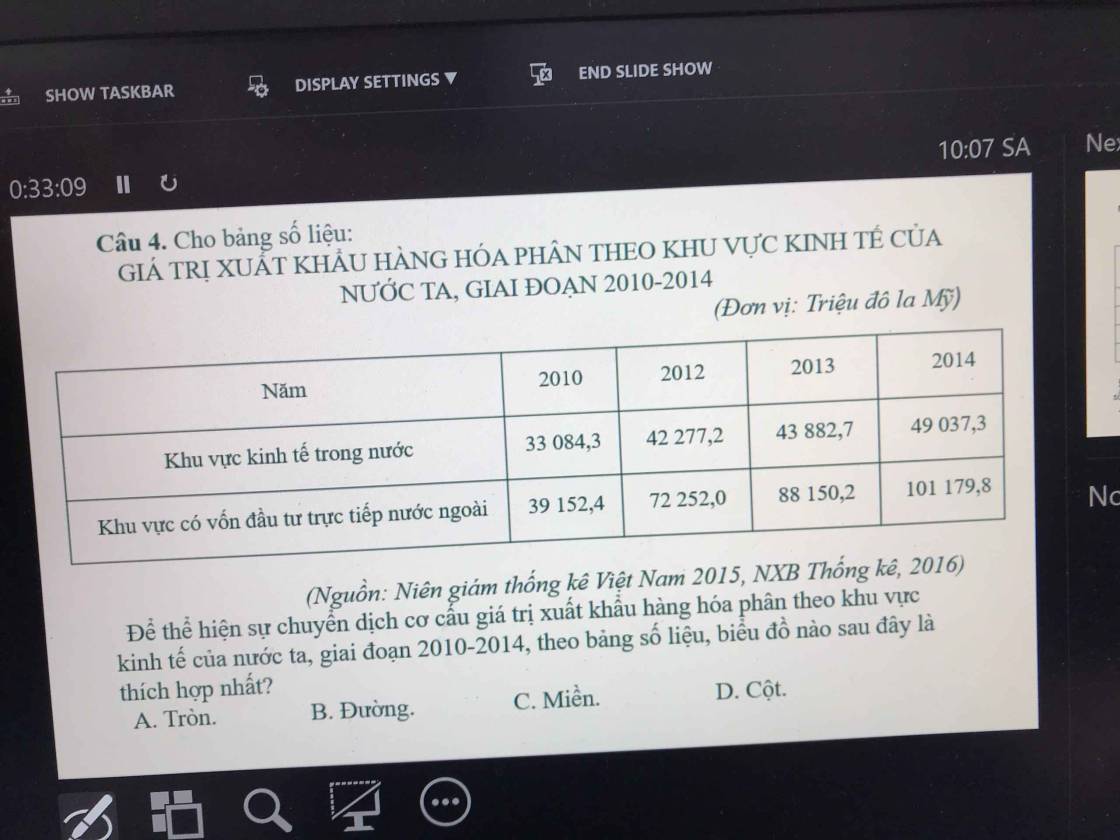

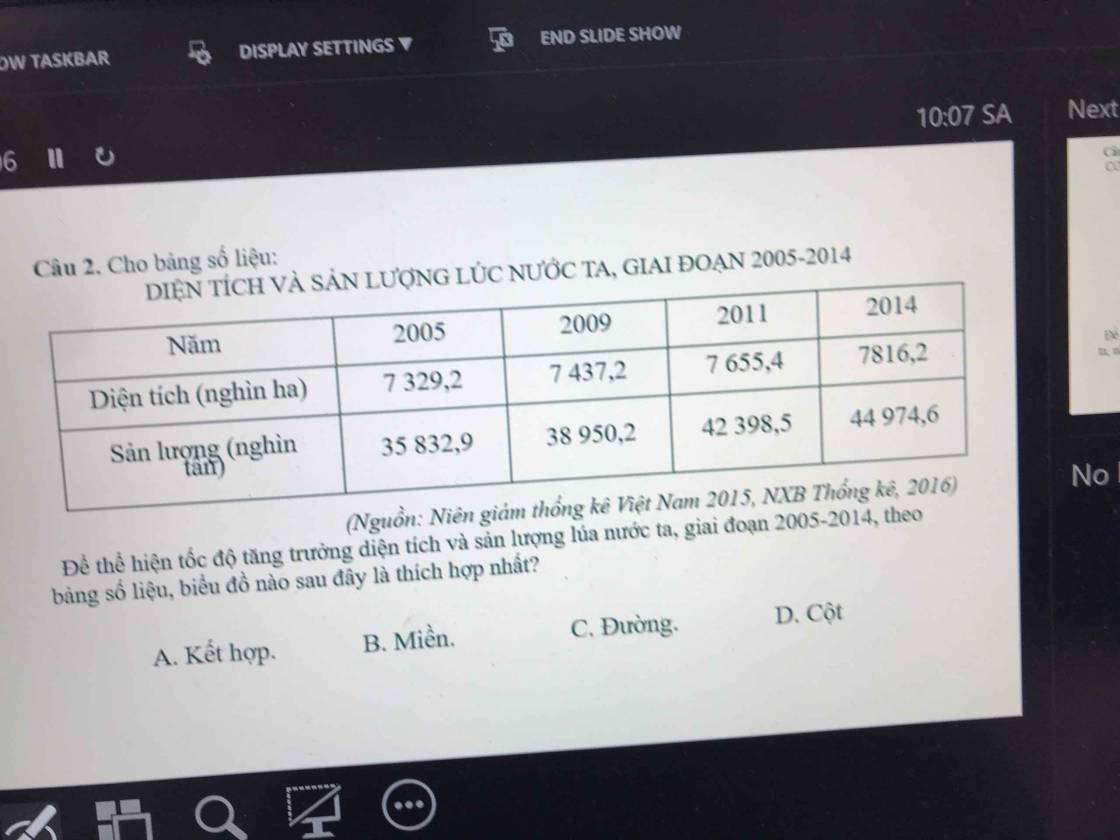
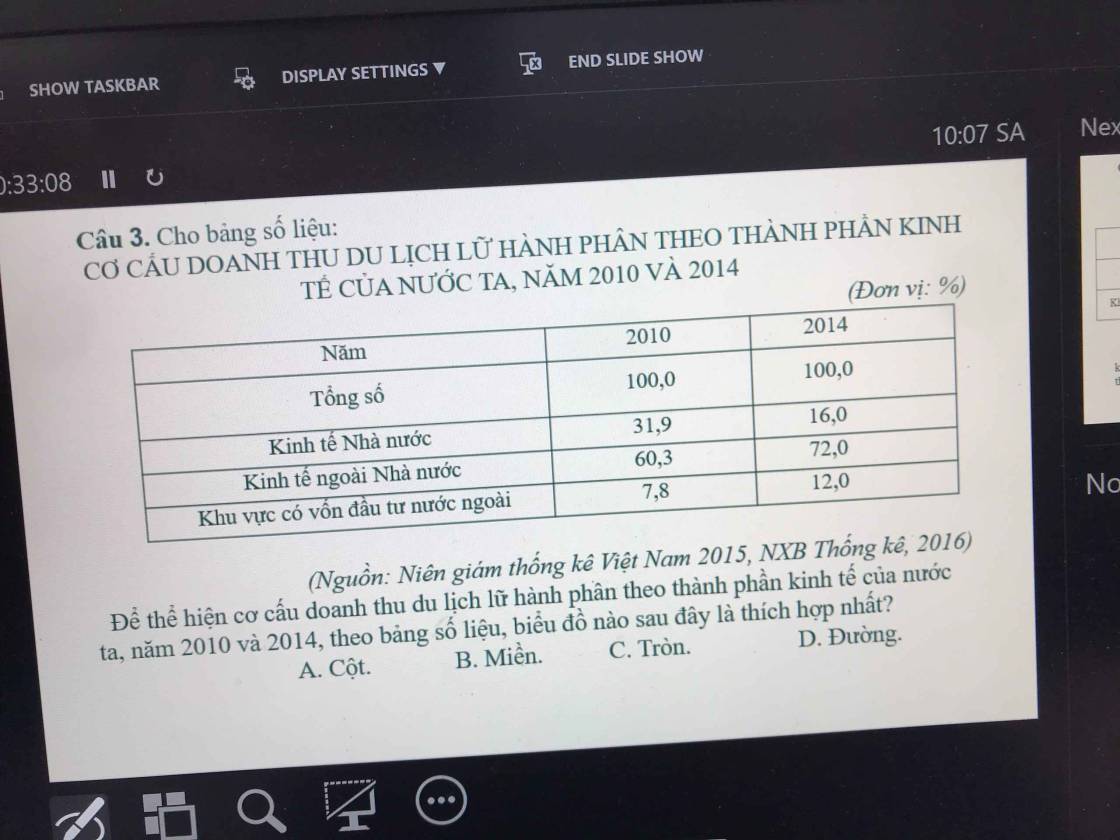
 cíu tui cíu tui
cíu tui cíu tui
a) \(\sqrt[]{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)
\(\Leftrightarrow\sqrt[]{3\left(x^2+2x+1\right)+4}+\sqrt{5\left(x^2+2x+1\right)+9}=-\left(x^2+2x+1\right)+5\)
\(\Leftrightarrow\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}=-\left(x+1\right)^2+5\left(1\right)\)
Ta có :
\(\left\{{}\begin{matrix}\sqrt[]{3\left(x+1\right)^2+4}\ge2,\forall x\in R\\\sqrt[]{5\left(x+1\right)^2+9}\ge3,\forall x\in R\end{matrix}\right.\)
\(\Rightarrow VT=\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}\ge5,\forall x\in R\)
\(VP=-\left(x+1\right)^2+5\le5,\forall x\in R\)
Dấu "=" xảy ra thì \(VT=VP=5\)
\(\left(1\right)\Leftrightarrow\left(x+1\right)^2=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Vậy nghiệm của phương trình đã cho là \(x=-1\)

cíu tui cíu tui
a: ΔOHB cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)HB
I là trung điểm của HB
=>\(IH=IB=\dfrac{HB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
ΔOIB vuông tại I
=>\(OB^2=OI^2+IB^2\)
=>\(OB^2=3^2+4^2=25\)
=>OB=5(cm)
=>R=5(cm)
Xét tứ giác MAOI có
\(\widehat{MAO}+\widehat{MIO}=90^0+90^0=180^0\)
=>MAOI là tứ giác nội tiếp đường tròn đường kính MO
Tâm là trung điểm của MO
b: Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó; ΔAHB vuông tại H
=>AH\(\perp\)HB tại H
=>AH\(\perp\)MB tại H
Xét ΔMAB vuông tại A có AH là đường cao
nên \(MA^2=MH\cdot MB\)
c: Xét (O) có
MA,MK là tiếp tuyến
Do đó: MA=MK
mà OA=OK
nên MO là đường trung trực của AK
\(MA^2=MH\cdot MB\)
MA=MK
Do đó: \(MK^2=MH\cdot MB\)
=>\(\dfrac{MK}{MH}=\dfrac{MB}{MK}\)
Xét ΔMKB và ΔMHK có
\(\dfrac{MK}{MH}=\dfrac{MB}{MK}\)
\(\widehat{KMB}\) chung
Do đó: ΔMKB đồng dạng với ΔMHK
=>\(\widehat{MBK}=\widehat{MHK}\)

cíu tui cíu tui
a: Vì y=ax+5//y=2x nên ta có:
\(\left\{{}\begin{matrix}a=2\\b< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=2\\5< >0\left(đúng\right)\end{matrix}\right.\)
=>a=2
b: Thay x=-1 và y=3 vào y=x+b, ta được:
\(b-1=3\)
=>b=1+3=4
Vậy: b=4
c: (d1): y=2x+5
(d2): y=x+4
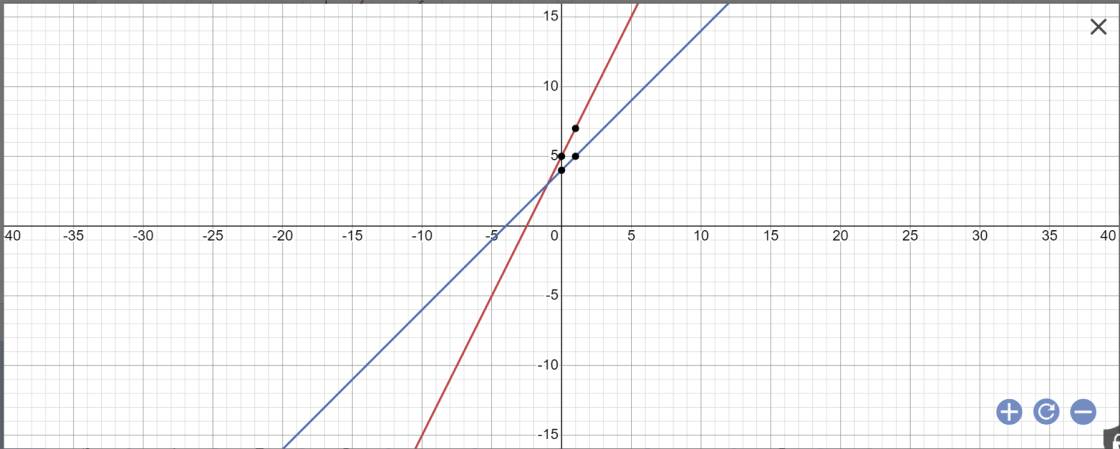
c: tọa độ điểm C là:
\(\left\{{}\begin{matrix}2x+5=x+4\\y=x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-x=4-5\\y=x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=-1+4=3\end{matrix}\right.\)
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{5}{2}\\y=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=0-4=-4\end{matrix}\right.\)
vậy:B(-4;0); C(-5/2;0); A(-1;3)
d: \(BC=\sqrt{\left(-\dfrac{5}{2}+4\right)^2+\left(0-0\right)^2}=1,5\)
\(BA=\sqrt{\left(-1+4\right)^2+\left(3-0\right)^2}=\sqrt{3^2+3^2}=3\sqrt{2}\)
\(AC=\sqrt{\left(-\dfrac{5}{2}+1\right)^2+\left(0-3\right)^2}=\sqrt{\left(-1,5\right)^2+\left(-3\right)^2}=\dfrac{3\sqrt{5}}{2}\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+BC+AC=1,5+3\sqrt{2}+\dfrac{3\sqrt{5}}{2}\)
Xét \(\Delta\)ABC có
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{18+11,25-2,25}{2\cdot3\sqrt{2}\cdot\dfrac{3\sqrt{5}}{2}}=\dfrac{27}{9\sqrt{10}}=\dfrac{3}{\sqrt{10}}\)
=>\(sinBAC=\sqrt{1-cos^2BAC}=\dfrac{1}{\sqrt{10}}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot3\sqrt{2}\cdot\dfrac{3\sqrt{5}}{2}\cdot\dfrac{1}{\sqrt{10}}=\dfrac{9}{4}\)
 cíu tui cíu tui
cíu tui cíu tui
a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=4\cdot9=36\)
=>\(AH=\sqrt{36}=6\left(cm\right)\)
b: Xét (O) có
ΔAEH nội tiếp
AH là đường kính
Do đó; ΔAEH vuông tại E
=>HE\(\perp\)AE tại E
=>HE\(\perp\)AB tại E
Xét (O) có
ΔAFH nội tiếp
AH là đường kính
Do đó; ΔAFH vuông tại F
=>HF\(\perp\)FA tại F
=>HF\(\perp\)AC tại F
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
c: Ta có: ΔHEB vuông tại E
mà EM là đường trung tuyến
nên EM=HM
=>\(\widehat{MHE}=\widehat{MEH}\)
mà \(\widehat{MHE}=\widehat{ACB}\)(hai góc đồng vị, HE//AC)
nên \(\widehat{MEH}=\widehat{ACB}\)
Ta có: AEHF là hình chữ nhật
=>\(\widehat{FEH}=\widehat{FAH}\)
mà \(\widehat{FAH}=\widehat{ABC}\left(=90^0-\widehat{HCA}\right)\)
nên \(\widehat{FEH}=\widehat{ABC}\)
\(\widehat{MEF}=\widehat{MEH}+\widehat{FEH}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
Vì AEHF là hình chữ nhật
nên AEHF nội tiếp đường tròn đường kính AH và EF
=>EF là đường kính của (O)
Xét (O) có
EF là đường kính
EM\(\perp\)EF tại E
=>EM là tiếp tuyến của (O)
cíu tui cíu tui ToT
Bài 1
1)\(K+H_2O\xrightarrow[]{}KOH\)(phản ứng hoá hợp)
3)\(Fe_2O_3+3H_2\xrightarrow[]{t^0}2Fe+3H_2O\)(phản ứng thế)
4)\(4Fe+3O_2\underrightarrow{t^0}2Fe_2O_3\)(phản ứng hoá hợp)
5)\(2Cu+O_2\xrightarrow[]{t^0}2CuO\)(phản ứng hoá hợp)
6)\(Na+H_2O\xrightarrow[]{}NaOH+H_2\)(phản ứng thế)
7)\(P_2O_5+3H_2O\xrightarrow[]{}2H_3PO_4\)(phản ứng hoá hợp)
8)\(SO_3+H_2O\xrightarrow[]{}H_2SO_4\)(phản ứng hoá hợp)
9)\(2H_2+O_2\xrightarrow[]{t^0}2H_2O\)(phản ứng hoá hợp)
10)\(Zn+2HCl\xrightarrow[]{}ZnCl_2+H_2\)(phản ứng thế)