31.

\(y'=4x^3+1\)

Tiếp tuyến vuông góc với \(d\) nên có hệ số góc \(k=5\)

Gọi hoành độ tiếp điểm là \(x_0\Rightarrow4x_0^3+1=5\Rightarrow x_0^3=1\)

\(\Rightarrow x_0=1\Rightarrow y_0=2\)

Phương trình: \(y=5\left(x-1\right)+2\Leftrightarrow y=5x-3\)

33.

Vận tốc của chất điểm: \(v\left(t\right)=S'\left(t\right)=5-6t\)

\(v\left(t\right)=3\Rightarrow5-6t=3\Rightarrow t=\dfrac{1}{3}\)

\(\Rightarrow S=5.\dfrac{1}{3}-3.\left(\dfrac{1}{3}\right)^2=1,33\left(m\right)\)

a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:

\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)

\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)

Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)

Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)

\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)

Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)

Câu 1:

\(\left\{{}\begin{matrix}y-2x< =2\\2y-x>=4\\x+y< =5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y< =2x+2\\2y>=x+4\\y< =-x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y< =2x+2\\y< =-x+5\\y>=\dfrac{1}{2}x+2\end{matrix}\right.\)

y<=2x+2

=>y-2x-2<=0

Vẽ đường thẳng y=2x+2

Khi x=0 và y=0 thì \(y-2x-2=0-0-2=-2< =0\)(đúng)

=>Miền nghiệm của BPT y<=2x+2 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)

y<=-x+5

=>x+y-5<=0

Khi x=0 và y=0 thì \(x+y-5=0+0-5< =0\)(đúng)

=>Miền nghiệm của BPT y<=-x+5 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)

y>=1/2x+2

=>\(-\dfrac{1}{2}x+y-2>=0\)

Khi x=0 và y=0 thì \(-\dfrac{1}{2}x+y-2=-\dfrac{1}{2}\cdot0+0-2=-2< 0\)

=>O(0;0) không thỏa mãn BPT \(-\dfrac{1}{2}x+y-2>=0\)

=>Miền nghiệm của BPT \(y>=\dfrac{1}{2}x+2\) là nửa mặt phẳng chứa biên nhưng không chứa điểm O(0;0)

Vẽ đồ thị:

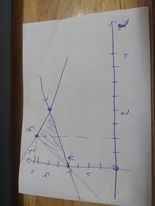
Theo hình vẽ, ta có: Miền nghiệm của hệ BPT sẽ là ΔABC, với A(0;2); B(1;4); C(2;3)

Khi x=0 và y=2 thì F=2-0=2

Khi x=1 và y=4 thì F=4-1=3

Khi x=2 và y=3 thì F=3-2=1

=>Chọn A

24.

Đường thẳng có 1 vtcp là \(\overrightarrow{u}=\left(2;-5\right)\)

25.

\(a^2=b^2+c^2-2bc.cosA\)

26.

A là mệnh đề sai, công thức đúng: \(S=\dfrac{1}{2}ab.sinC\)

27.

\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}=\sqrt{3^2+4^2-2.3.4.cos60^0}=\sqrt{13}\)

28.

\(\widehat{A}=180^0-\left(35^030'+45^0\right)=99^030'\)

Áp dụng định lý hàm sin:

\(\dfrac{a}{sinA}=\dfrac{b}{sinB}\Rightarrow b=\dfrac{a.sinB}{sinA}=\dfrac{12,5.sin\left(35^030'\right)}{sin\left(99^030'\right)}=7,36\left(m\right)\)

23.

Ta sẽ tìm điểm \(I\left(a;b;c\right)\) sao cho \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\) (1)

\(\left\{{}\begin{matrix}\overrightarrow{IA}=\left(-2-a;2-b;6-c\right)\\\overrightarrow{IB}=\left(-3-a;1-b;8-c\right)\\\overrightarrow{IC}=\left(-1-a;-b;7-c\right)\\\overrightarrow{ID}=\left(1-a;2-b;3-c\right)\end{matrix}\right.\)

\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\left(-5-4a;5-4b;24-4c\right)\)

(1) thỏa mãn khi: \(\left\{{}\begin{matrix}-5-4a=0\\5-4b=0\\24-4c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{4}\\b=\dfrac{5}{4}\\c=6\end{matrix}\right.\)

\(\Rightarrow I\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\)

Khi đó:

\(T=MA^2+MB^2+MC^2+MD^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{ID}\right)^2\)

\(=4MI^2+IA^2+IB^2+IC^2+ID^2+2\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\right)\)

\(=4MI^2+IA^2+IB^2+IC^2+ID^2\) (do \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\))

\(IA^2+IB^2+IC^2+ID^2\) cố định nên \(T_{min}\) khi \(MI_{min}\)

\(\Leftrightarrow M\) trùng I

\(\Rightarrow M\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\Rightarrow x+y+z=-\dfrac{5}{4}+\dfrac{5}{4}+6=6\)

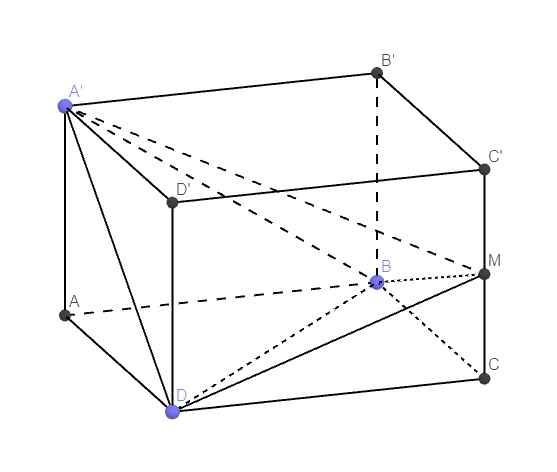
24.

\(a+b=4\Rightarrow b=4-a\)

ABCD là hình chữ nhật \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)

\(\Rightarrow C\left(a;a;0\right)\)

Tương tự ta có: \(C'\left(a;a;b\right)\)

M là trung điểm CC' \(\Rightarrow M\left(a;a;\dfrac{b}{2}\right)\)

\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{A'B}=\left(a;0;-b\right)=\left(a;0;a-4\right)\\\overrightarrow{A'D}=\left(0;a;-b\right)=\left(0;a;a-4\right)\\\overrightarrow{A'M}=\left(a;a;-\dfrac{b}{2}\right)=\left(a;a;\dfrac{a-4}{2}\right)\end{matrix}\right.\)

Theo công thức tích có hướng:

\(\left[\overrightarrow{A'B};\overrightarrow{A'D}\right]=\left(-a^2+4a;-a^2+4a;a^2\right)\)

\(\Rightarrow V=\dfrac{1}{6}\left|\left[\overrightarrow{A'B};\overrightarrow{A'D}\right].\overrightarrow{A'M}\right|=\dfrac{1}{6}\left|a\left(-a^2+4a\right)+a\left(-a^2+4a\right)+\dfrac{a^2\left(a-4\right)}{2}\right|\)

\(=\dfrac{1}{4}\left|a^3-4a^2\right|=\dfrac{1}{4}\left(4a^2-a^3\right)\)

Xét hàm \(f\left(a\right)=\dfrac{1}{4}\left(4a^2-a^3\right)\) trên \(\left(0;4\right)\)

\(f'\left(a\right)=\dfrac{1}{4}\left(8a-3a^2\right)=0\Rightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=\dfrac{8}{3}\end{matrix}\right.\)

\(\Rightarrow f\left(a\right)_{max}=f\left(\dfrac{8}{3}\right)=\dfrac{64}{27}\)

Hình vẽ bài 24:

Câu C bạn nhé!!

11. 

Đường tròn (C) tâm \(I\left(4;3\right)\) bán kính \(R=\sqrt{2}\)

\(d\left(I;\Delta\right)=\dfrac{\left|4+3-11\right|}{\sqrt{1^2+1^2}}=2\sqrt{2}\)

\(\Rightarrow d\left(M;\Delta\right)_{max}=R+d\left(I;\Delta\right)=\sqrt{2}+2\sqrt{2}=3\sqrt{2}\)