g) \(B=\dfrac{x^2+x+1}{x-2}=\dfrac{x^2-2x+3x-6+7}{x-2}=\dfrac{x\left(x-2\right)+3\left(x-2\right)+7}{x-2}=x+3+\dfrac{7}{x-2}=x-2+\dfrac{7}{x-2}+5\ge2\sqrt{\left(x-2\right).\dfrac{7}{x-2}}+5=2\sqrt{7}+5\)

\(B=2\sqrt{7}+5\Leftrightarrow\sqrt{x-2}=\sqrt{\dfrac{7}{x-2}}\Leftrightarrow x=2+\sqrt{7}\)

-Vậy \(B_{min}=2\sqrt{7}+5\)

\(B=\dfrac{9-3x+x^2-25-x^2+1}{\left(x+5\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{7\left(x-2\right)}=\dfrac{-3x-15}{\left(x+5\right)}\cdot\dfrac{\left(x+1\right)}{7\left(x-2\right)}\)

\(=\dfrac{-3x-3}{7\left(x-2\right)}\)

g: \(B=\dfrac{-3}{7}\cdot\dfrac{x+1}{x-2}\)

\(=\dfrac{-3}{7}\left(\dfrac{x-2+3}{x-2}\right)\)

\(=\dfrac{-3}{7}\left(x-2+\dfrac{3}{x-2}\right)>=-\dfrac{3}{7}2\sqrt{3}=\dfrac{-6\sqrt{3}}{7}\)

Dấu = xảy ra khi (x-2)^2=3

=>x=căn 3+2

f: Thay x=0 và y=5 vào (d), ta được: 

m-1=5

hay m=6

e: Thay x=1 và y=4 vào (d),ta được:

2m+3+m-1=4

=>3m+2=4

hay m=2/3

ủa đây là dạng toán lớp 6 mà

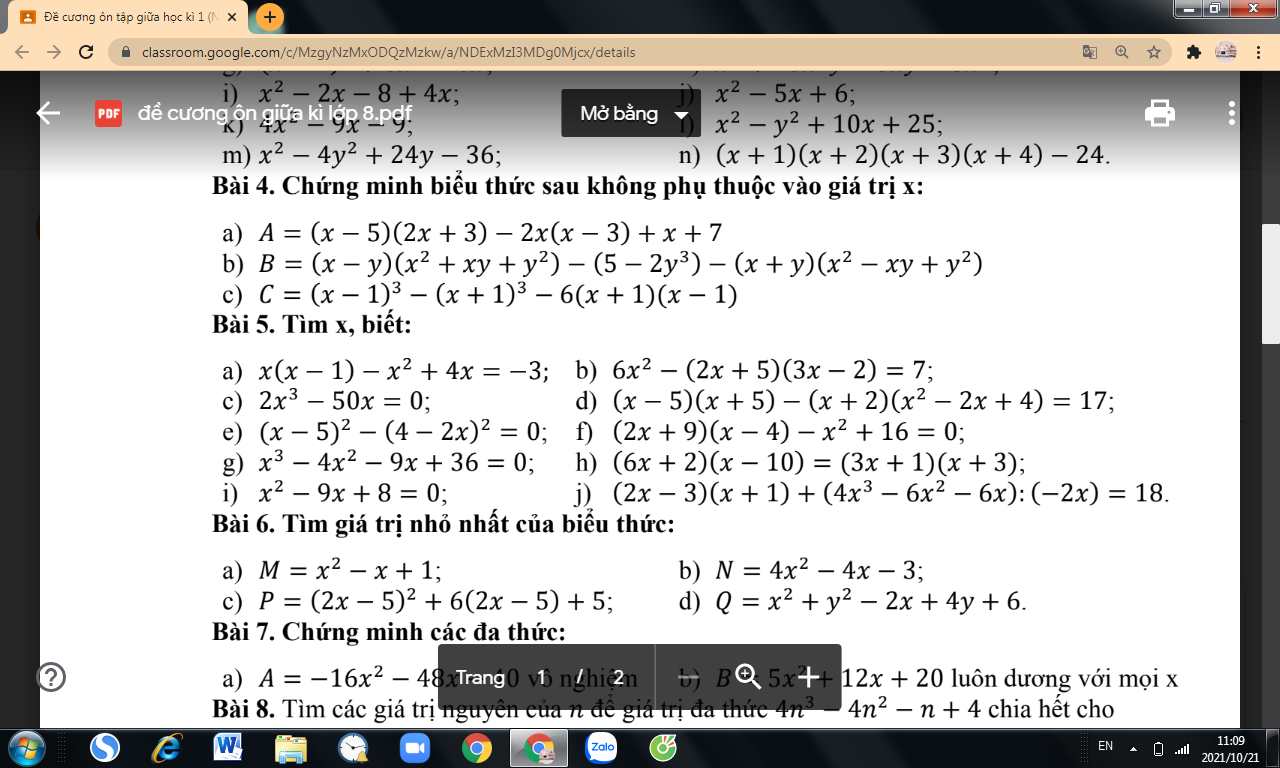
c: \(2x^3-50x=0\)

\(\Leftrightarrow2x\left(x-5\right)\left(x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)

Câu 6: 

a: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có 

\(\widehat{B}\) chung

Do đó: ΔBAC∼ΔBHA

\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)

6a.

$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$

$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$

Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

Nãy ghi nhầm =="

a)Hđ gđ là nghiệm pt

`x^2=2x+2m+1`

`<=>x^2-2x-2m-1=0`

Thay `m=1` vào pt ta có:

`x^2-2x-2-1=0`

`<=>x^2-2x-3=0`

`a-b+c=0`

`=>x_1=-1,x_2=3`

`=>y_1=1,y_2=9`

`=>(-1,1),(3,9)`

Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`

b)

Hđ gđ là nghiệm pt

`x^2=2x+2m+1`

`<=>x^2-2x-2m-1=0`

PT có 2 nghiệm pb

`<=>Delta'>0`

`<=>1+2m+1>0`

`<=>2m> -2`

`<=>m> 01`

Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`

Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`

`=>x_1^2+x_2^2=14`

`<=>(x_1+x_2)^2-2x_1.x_2=14`

`<=>4-2(-2m-1)=14`

`<=>4+2(2m+1)=14`

`<=>2(2m+1)=10`

`<=>2m+1=5`

`<=>2m=4`

`<=>m=2(tm)`

Vậy `m=2` thì ....