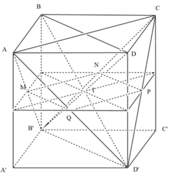
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a và G là trọng tâm tam giác A'BC. Tính 3AG^2.Ai giúp em với ạ❤

Những câu hỏi liên quan
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB=a, góc giữa 2 mặt phẳng (A'BC) và (ABC) bằng 60 độ. Gọi G là trọng tâm của tam giác A'BC.
Tính thể tích của khối lăng trụ đã cho và bán kính mặt cầu ngoại tiếp tứ diện GABC theo a
_ Thể tích khối lăng trụ :
Gọi D là trung điểm của BC ta có : \(BC\perp AD\Rightarrow BC\perp A'D\Rightarrow\widehat{ADA'}=60^0\)
Ta cso \(AA'=AD.\tan\widehat{ADA'}=\frac{3a}{2};S_{ABC}=\frac{a^2\sqrt{3}}{4}\)
Do đó \(V_{ABC.A'B'C'=}S_{ABC}.AA'=\frac{3a^2\sqrt{3}}{8}\)
- Bán kính mặt cầu ngoại tiếp tứ diện GABC :
Ta có I là giao điểm của GH với đường trung trực của AG trong mặt phẳng (AGH)
Gọi E là trung điểm của AG, ta có :
\(R=GI=\frac{GE.GA}{GH}=\frac{GA^2}{2GH}\)
Ta có :
\(GH=\frac{AA'}{3}=\frac{a}{2};AH=\frac{a\sqrt{3}}{3};GA^2=GH^2+AH^2=\frac{7a^2}{12}\)
Do đó \(R=\frac{7a^2}{2.12}.\frac{2}{a}=\frac{7a}{12}\)
Đúng 0
Bình luận (1)
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh a. Tính khoảng cách từ điểm A đến mặt phẳng (ABC) theo a. A.
a
2
2
B.
a
3
3
C.
a
3...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Tính khoảng cách từ điểm A đến mặt phẳng (A'BC) theo a.
A. a 2 2
B. a 3 3
C. a 3 2
D. a 2 3
Đáp án A
Ta có: 1 d 2 = 1 A B 2 + 1 A A ' 2 = 2 a 2 ⇒ d = a 2 2 .
Đúng 0
Bình luận (0)
Cho hình lăng trụ tam giác ABC A'B'C'. Gọi K M N E lần lượt là trung điểm của các cạnh CC' AB AA' và BB' . G là trọng tâm tam giác ABC, I là điểm thuộc đoạn BC sao cho BI = 1/3 BC. CMR
a/ (MNC) // (A'BK)
b/ (MNK) // (A'BC')
c/ ( GKN) // (A'IC')
Giúp mình câu c với ạ
Mọi người cho em hỏi là bài toán Cho hình lập phương ABCD.A'B'C'D' có AB =a .Gọi O là tâm của hình vuông ABCD .Tính khoảng cách giữa 2 đường A'O và BC Bài này muốn giải bằng phương pháp trục tọa độ thì làm sao ạ
Cho lăng trụ
A
B
C
D
.
A
B
C
D
có đáy là hình vuông cạnh
a
3
. Hình chiếu vuông góc của điểm A lên mặt phẳng
(
A
B
C
D
)
trùng với tâm O của hình vuông
A
B
C
D
. Biết rằng...
Đọc tiếp
Cho lăng trụ A B C D . A ' B ' C ' D ' có đáy là hình vuông cạnh a 3 . Hình chiếu vuông góc của điểm A lên mặt phẳng ( A ' B ' C ' D ' ) trùng với tâm O của hình vuông A ' B ' C ' D ' . Biết rằng khoảng cách từ trọng tâm G của tam giác AB’D’ đến mặt phẳng (AA’D) bằng a 2 . Khoảng cách từ điểm O đến mặt phẳng ( A D C ' B ' ) bằng
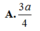

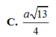
![]()
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi O là tâm của mặt đáy ABCD.
a) Chứng minh O.A'B'C'D' là hình chóp tứ giác đều.
b) Gọi thể tích hình chóp đều O.A'B’C'D' là V' và thể tích hình lập phương là V. Tính tỉ số V'/V
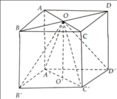
a) Bốn tam giác OAA', OBB', OCC', ODD' là các tam giác vuông bằng nhau nên suy ra OA' = OB' = OC' = OD'.
Hình chóp O.A'B'C'D' là hình chóp đều vì có các mặt bên là tam giác cân và đáy là đa giác đều.
b) Thể tích của của hình chóp O.A'B'C'D' là:
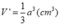
Thể tích hình lập phương:
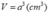
Vậy V ' V = 1 3
Đúng 0
Bình luận (0)
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh a. Xét tứ diện ABCD. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được. A.
a
2
3
.
B. ...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Xét tứ diện AB'CD'. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được.
A. a 2 3 .
B. 2 a 2 3 .
C. a 2 2 .
D. 3 a 2 4 .
Cho hình lập phương ABCD.ABCD cạnh a. Xét tứ diện ABCD. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Xét tứ diện AB'CD'. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được
![]()
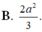
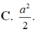

Cho hình lập phương ABCD.ABCD cạnh a. Xét tứ diện ABCD. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được A.
a
2
3
.
B.
2
a
2
3
.
C.
a...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Xét tứ diện AB'CD'. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được
A. a 2 3 .
B. 2 a 2 3 .
C. a 2 2 .
D. 3 a 2 4 .