Tìm x y sao cho bt sau đạt giá trị nhỏ nhất
M= 8x2+yy2—4xy—16x+17
Giup minh voi
tìm x và y sao cho biểu thức M= 8x^2+y^2-4xy-16x+17 đạt giá trị nhỏ nhất?
Ta có: M = \(8x^2+y^2-4xy-16x+17\)
<=> M = \(\left(4x^2-4xy+y^2\right)+\left(4x^2-16x+16\right)+1\)
<=> M = \(\left(2x-y\right)^2+\left(2x-4\right)^2+1\)
Vì \(\left\{{}\begin{matrix}\left(2x-y\right)^2\ge0\\\left(2x-4\right)^2\ge0\end{matrix}\right.\) => M \(\ge\) 1
=> Dấu = xảy ra <=> \(\left\{{}\begin{matrix}2x-y=0\\2x-4=0\end{matrix}\right.\) <=> x = 2; y = 4
=> GTNN của M = 1 khi x = 2; y= 4
a) Tìm x để phân thức M = 8 x 2 − 4 x + 12 đạt giá trị lớn nhất;
b) Tìm x để phân thức N = − 5 x 2 + 2 x + 11 đạt giá trị nhỏ nhất.
a) * Nếu M ≥ a ⇔ 1 M ≤ 1 a ;
* Nếu M ≤ a ⇔ 1 M ≥ 1 a ;
b) Ta có x 2 - 4x + 12 = ( x - 2 ) 2 + 8 ≥ 8 hay 1 x 2 + 2 x + 11 ≤ 1 10 ⇒ N ≥ − 1 2
Giá trị nhỏ nhất của N = − 1 2 khi x = -1.
Cho biểu thức A=3x²+4xy+5y²+6x+7y+4
Tìm giá trị nhỏ nhất của A. Với giá trị nào của x,y thì A đạt giá trị nhỏ nhất .
Cho phương trình bậc hai x^2-mx+m-3=0 Chứng minh rằng phương trình luôn có nghiệm với mọi m Tìm các giá trị m để phương trình có hai nghiệm x1 x2 sao cho bt A=2(x1+x2)-x1×x2) đạt giá trị nhỏ nhất
Ptr có:`\Delta=(-m)^2-4(m-3)=m^2-4m+12=(m-2)^2+8 > 0 AA m`
`=>` Ptr luôn có nghiệm `AA m`
`=>` Áp dụng Viét có:`{(x_1+x_2=[-b]/a=m),(x_1.x_2=c/a=m-3):}`
Ta có:`A=2(x_1 ^2+x_2 ^2)-x_1.x_2`
`<=>A=2[(x_1+x_2)^2-2x_1.x_2]-x_1.x_2`
`<=>A=2[m^2-2(m-3)]-(m-3)`
`<=>A=2(m^2-2m+6)-m+3`
`<=>A=2m^2-4m+12-m+3=2m^2-5m+15`
`<=>A=2(m^2-5/2+15/2)`
`<=>A=2[(m-5/4)^2+95/16]`
`<=>A=2(m-5/4)^2+95/8`
Vì `2(m-5/4)^2 >= 0 AA m<=>2(m-5/4)^2+95/8 >= 95/8 AA m`
Hay `A >= 95/8 AA m`
Dấu "`=`" xảy ra`<=>(m-5/4)^2=0<=>m=5/4`
Vậy `GTN N` của `A` là `95/8` khi `m=5/4`
Đề liệu cs sai 0 bạn nhỉ, ở cái biểu thức `A` í chứ nếu đề vậy thì 0 tìm đc GTNN đâu (Theo mik thì là vậy)
tìm giá trị nhỏ nhất của đa thức sau:
4x^2+2y^2+4xy-16x-12y+5
Đặt \(K=4x^2+2y^2+4xy-16x-12y+5\)
\(K=\left(4x^2+4xy+y^2\right)+y^2-16x-12y+5\)
\(K=\left[\left(2x+y\right)^2-2\left(2x+y\right).4+16\right]+\left(y^2-4y+4\right)-15\)
\(K=\left(2x+y-4\right)^2+\left(y-2\right)^2-15\)
Mà \(\left(2x+y-4\right)^2\ge0\forall x;y\)
\(\left(y-2\right)^2\ge0\forall y\)
\(\Rightarrow K\ge-15\)
Dấu "=" xảy ra khi : \(\hept{\begin{cases}2x+y-4=0\\y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\)
Vậy \(K_{Min}=-15\Leftrightarrow\left(x;y\right)=\left(1;2\right)\)
Tìm giá trị lớn nhất của hàm số f (x) = x 3 - 8 x 2 + 16 x - 9 trên đoạn [1;3]
A. m a x [ 1 ; 3 ] f ( x ) = - 6
B. m a x [ 1 ; 3 ] f ( x ) = 13 27
C. m a x [ 1 ; 3 ] f ( x ) = 0
D. m a x [ 1 ; 3 ] f ( x ) = 5
Cho A= {14;21; 23;34;19;0}. Tìm x, y , thuộc A , x và y khác nhau sao cho :
a. Tổng x+y đạt giá trị lớn nhất. b. Tổng x+y đạt giá trị nhỏ nhất.
a: Vì A là tập hợp của các số không âm nên để \(\left(x+y\right)_{max}\) và \(x,y\in A\)
thì x,y là hai số lớn nhất trong A
=>x=34 và y=23
b: Vì B là tập hợp của các số không âm nên để \(\left(x+y\right)_{min}\) và \(x,y\in A\)
thì x,y là hai số nhỏ nhất trong A
=>x=0 và y=14
Tìm giá trị lớn nhất và giá trị nhỏ nhất của y = 8 x 4 - 8 x 2 + 1 với x ∈ 1 2 ; 1 .
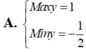
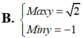
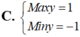
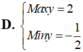
Tìm giá trị nhỏ nhất của biểu thức:
\(A=13x^2+y^2+4xy-2y-16x+2015\)
\(A=13x^2+y^2+4xy-2y-16x+2015\)
\(A=\left(4x^2-4x+1\right)+2y\left(2x-1\right)+y^2+\left(9x^2-12x+4\right)+2010\)
\(A=\left(2x-1\right)^2+2y\left(2x-1\right)+y^2+\left(3x-2\right)^2+2010\)
\(A=\left(2x-1+y\right)^2+\left(3x-2\right)^2+2010\)
Đến đây bạn tự làm nốt nhé~
không làm được thì ib