Cho ∆ABC vuông tại A, phân giác BD(D thuộc AC) Vẽ DE vuông góc BC( D thuộc BC). Chứng minh rằng a, ∆ABC=∆EBD b, BD là đường trung trực của AE c, Gọi F là giao điểm của BA và ED chứng minh DE

Những câu hỏi liên quan
Cho tam giác abc vuông tại A có BD là phân giác, kẻ DE vuông góc với BC(E thuộc BC). Gọi F là giao điểm của AB và ĐE. Chứng minh rằng a) tam giác ABD = tam giác EBD b) BĐ là đường trung trực của AE c) BD vuông góc FC d) AE + FC < 2AC
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: BA=BE
DA=DE
=>BD là trung trực của AE
c: Xét ΔBFC có
FE,CA là đường cao
FE cắt CA tại D
=>D là trực tâm
=>BD vuông góc FC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, vẽ BD là tia phân giác của ABC (D thuộc AC. Trên cạnh BC lấy điểm E sao cho BE=BA. Gọi I là giao điểm của BD và AE. a) Chứng minh: tam giác ABD= tam giác EBD. b) Chứng minh: DE=AD và DE vuông góc BC.
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên DA=DE
Ta có: ΔABD=ΔEBD
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE⊥BC
Đúng 2
Bình luận (0)
a: Xét ΔABD và ΔEBD có
BA=BE
ˆABD=ˆEBDABD^=EBD^
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên DA=DE
Ta có: ΔABD=ΔEBD
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A; BD là phân giác của góc B (D thuộc AC). trên tia BC lấy điểm E sao cho BA = BE. a) chứng minh rằng: tam giác ABD = tam giác EBD và DE vuông góc với BE. b) chứng minh: BD là đường trung trực của đoạn tthẳng AE. c) Kẻ AH vuông góc với BC tại H. CHỨNG minh rằng: AD < DH

a)
và có:
BA = BE (gt)
(BD là tia phân giác góc B)
BD là cạnh chung
(c.g.c)
(hai góc tương ứng)
DE BE
b) và có:
Đúng 3
Bình luận (0)
Cho tam giác ABC có AB = 6cm ; AC = 8cm ; BC = 10cm
a) Chứng minh tam giác ABC vuông tại A
b) Vẽ tia phân giác BD của góc ABC (D thuộc AC), từ D vẽ DE vuông góc với BC (E thuộc BC) Chứng minh DA =DE
c) Kéo dài ED và BA cắt nhau tại F. Chứng minh DF>DE
d) Chứng minh đường thẳng BD là đường trung trực của đoạn thẳng FC
ta có : BC2 = 102 = 100
AC2 +AB2 =62 + 82 =36 +64 = 100
BC2 =AC2 + AB2
suy ra tam giác ABC vuông tại A ( định lý pytago đảo )
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
b. BD là đường trung trực của AE
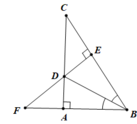
b. Ta có AB = BE ⇒ B nằm trên đường trung trực của AE (0.5 điểm)
Do ∆ABD = ∆EBD nên AD = DE (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE
Vậy BD là đường trung trực của AE (0.5 điểm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có BD là đường phân giác của góc B. Kẻ DE BC (E BC). Gọi F là giao điểm của tia BA và tia ED. Chứng minh: a/ ABD = EBD. Từ đó suy ra BD là đường trung trực của AE. b/ AD < DC. c/ AE // FC.
a: XétΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE và DA=DE
hay BD là đường trung trực của AE
b: Ta có: AD=DE
mà DE<DC
nên AD<CD
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB =6cm, AC=8cm, BC=10cm
a) chứng ninh tam giác ABC vuông tại A
b) vẽ tia phân giác BD của góc ABC ( D thuộc AC) từ D vẽ DE vuông BC (E thuộc BC) .Chứng minh DA=DE
c) kéo dài ED và BA cắt nhau tại F. Chứng minh DF>DE
d) Chứng minh đường thẳng BD là đường trung trực của đạn thẳng FC
Help!
a, AB = 6 => AB^2 = 6^2 = 36
AC = 8 => AC^2 = 8^2 = 64
=> AB^2 + AC^2 = 36 + 64 = 100
BC = 10 => BC^2 = 10^2 = 100
=> BC^2 = AB^2 + AC^2
=> tam giác ABC vuông tại A (định lí PTG đảo)
Đúng 0
Bình luận (0)
a, xét tam giác ABD và tam giác EBD có : BD chung
góc ABD = góc EBD do BD là phân giác
góc DAB = góc DEB = 90 do ...
=> tam giác ABD = tam giác EBD (ch - gn)
=> AD = ED (đn)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A có BD là phân giác, kẻ DE vuông góc với BC (E thuộc BC). Gọi F là giao điểm của AB và DE. Chứng minh rằng:
a. Tam giác ABD = tam giác EBD b.BD là đường trung trực của AE
c. AD < DC d. E, D, F thẳng hàng và BD vuông góc với CF
e. 2(AD + AF)>CF
a, Xét tam giác ABD và tam giác EBD có:
góc BAD=BED(tam giác abc vuông, DE vuông góc BC)
BD=BD(chung)
góc ABD=EBD (BD là phân giác)
=)tam giác ABD=tam giác EBD(cạnh huyền-góc nhọn)
vậy.....
b,gọi giao của AE và BD là O
ta có tam giác ABD=tam giác EBD
=)AB=BE ( 2 cạnh tưng ứng)
xét tam giác ABO và tam giác EBO có:
AB=BE (cmt)
góc ABO=EBO ( BD là phân giác)
BO=BO ( chung)
=)tam giác ABO=EBO (c-g-c)
=)AO=OE ( 2 cạnh tương ứng)(1)
AOB=EOB( 2 góc tương ứng)
mà AOB+EOB=180 độ ( 2 góc kề bù)
=)AOB=EOB=180:2=90độ
=)BO vuông góc AE (2)
từ(1) và (2)=)BO là trung trực AE
vậy....
c, Ta có tam giác DEC vuông tại E
=)DC>DE ( trong tam giác vuông cạnh huyền là cạnh lớn nhất)
mà DE=DA ( tam giác ABD= tam giác EBD)
=)DC>DA
hay DA<DC
vậy....
Đúng 0
Bình luận (0)
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔBAD=ΔBED
nên BA=BE và DA=DE
Ta có: BA=BE
nên B nằm trên đường trung trực của AE\(\left(1\right)\)
Ta có: DA=DE
nên D nằm trên đường trung trực của AE\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra BD là đường trung trực của AE
Đúng 0
Bình luận (0)
c: Ta có: DA=DE
mà DE<DC
nên DA<DC
d: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: AF=EC và DF=DC
Ta có: BA+AF=BF
BE+EC=BC
mà BA=BE
và AF=EC
nên BF=BC
Ta có: BF=BC
nên B nằm trên đường trung trực của CF\(\left(3\right)\)
Ta có: DF=DC
nên D nằm trên đường trung trực của CF\(\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra BD là đường trung trực của CF
hay BD\(\perp\)CF
Đúng 0
Bình luận (0)
Cho Tam giác ABC vuông tại A, biết AB=9cm,AC=12.Tia phân Giác BD ( D thuộc AC) Từ B kẻ DE vuông góc với BC Tính BC Chứng minh Tam giác ABD = Tam Giác EBD Chứng minh BD vuông góc với AE Gọi F là giao điểm của DE và BA.CHỨNG mình AE//CF
a: \(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
b: XétΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
c: ta có: ΔABD=ΔEBD
nên BA=BE và DA=DE
=>BD là đường trung trực của AE
hay BD\(\perp\)AE
Đúng 0
Bình luận (0)




















