a: Xét ΔAHB vuông tại H và ΔAHD vuông tại H có 

HB=HD

AH chung

Do đó: ΔAHB=ΔAHD

Suy ra: AB=AD

Xét ΔABD có AB=AD

nên ΔABD cân tại A

b: Xét ΔCHB vuông tại H và ΔCHD vuông tại H có 

CH chung

HB=HD

Do đó: ΔCHB=ΔCHD

Suy ra: CB=CD

c: Xét ΔDBC có 

BM là đường cao ứng với cạnh DC

CH là đường cao ứng với cạnh BD

BM cắt CH tại I

Do đó: I là trực tâm của ΔDCB

Suy ra: DI\(\perp\)BC

K lm mà đòi cs ăn thì ăn đầu buồy!!

Bạn chú ý viết cách phần cho và phần yêu cầu.

a/ Xét t/g ABI và t/g ADI có

AI : chung

\(\widehat{BAI}=\widehat{CAI}\) (AI là pg góc BAC)

AB = AD (GT)

=> t/g ABI = t/g ADI (c.g.c)

=> BI = DI (2 cạnh t/ứ)

b/ Có t/g ABI = t/g ADI

=> \(\widehat{ABI}=\widehat{ADI}\)(2 góc t/ứ)

=> \(180^o-\widehat{ABI}=180^o-\widehat{ADI}\)

=> \(\widehat{IBK}=\widehat{IDC}\) Xét t/g BIK và t/g DIC có

\(\widehat{IBK}=\widehat{IDC}\)

IB = DI (cmt)

\(\widehat{BIK}=\widehat{DIC}\)(đối đỉnh)

=> t/g BIK = t/g DIC (g.c.g)

c/ Có t/g BIK = t/g DIC

=> BK = DC (2 cạnh t/ứ) => AB + BK = DC + AD

=> AK = AC

=> t/g AKC cân tại A 

Mà AI là pg góc BAC (K thuộc AB)

=> AI đồng thời là đường cao t/g AKC

=> AI ⊥ KC Mà BH ⊥ KC

=> AI // BH

bạn tự vẽ hình nhá

Vì AI là tia phân giác ⇔ \(\widehat{BAI}=\widehat{DAI}=\dfrac{\widehat{BAC}}{2}\)

a) xét Δ ABI và ΔADI, có:

 AB=AD

\(\widehat{BAI}=\widehat{DAI}\)  (cmt)    

AI chung

⇒Δ ABI  =Δ ADI (c.g.c)

⇒BI=DI (2 cạnh t/ứng) (đpcm)

b) Do Δ ABI  =Δ ADI (cmt) ⇒ \(\widehat{ABI}=\widehat{ADI}\)

Có: \(\widehat{ABI}+\widehat{IBK}\) =180⁰ (2 góc kề bù)

      \(\widehat{ADI}+\widehat{IDC}\) =180⁰ (2 góc kề bù)

Mà \(\widehat{ABI}=\widehat{ADI}\) (cmt) ⇒ \(\widehat{IBK}=\widehat{IDC}\)

Vì \(\widehat{BIK}\) và \(\widehat{DIC}\) là 2 góc đối đỉnh ⇒ \(\widehat{BIK}\) =\(\widehat{DIC}\)

xét Δ BKI và Δ DCI có:

\(\widehat{IBK}=\widehat{IDC}\) (cmt)

BI=ID (cmt)

\(\widehat{BIK}\) =\(\widehat{DIC}\) (cmt)

⇒Δ BKI = Δ DCI (g.c.g) (đpcm)

c) Từ Δ BKI = Δ DCI (cmt) ⇒ BK=DC

Có AB=AD (gt) ; BK=DC (cmt)

⇔AB+BK=AD+DC

⇔AK=AC

⇒Δ ACK cân tại A.

Mà AI là phân giác của \(\widehat{KAC}\) (gt)

⇒AI vừa là đường phân giác vừa là đường cao của Δ ACK.

⇒AI ⊥ CK. mà BH ⊥ CK (gt)

⇒AI // BH (đpcm)

a)Xét \(\Delta ABD=\Delta IBD\left(ch-gn\right)\Rightarrow AB=BI;AD=DI.\)

b)Xét \(\Delta ABH=\Delta IBH\left(c-g-c\right)\Rightarrow AHB=IHB=90^0\)

Suy ra \(AI\perp BD\)

c)XÉT \(\Delta ADK=\Delta IDC\left(cgv-gnk\right)\Rightarrow KB=DC\)

d) vì \(BD//EI\Rightarrow DBI=BIE;DBI=BEI\)

HAY \(BIE=BEI\Rightarrow\Delta BIE\)CÂN TẠI B

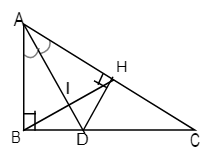
a) Xét ΔABD và ΔAHD có: 

∠ABD = ∠AHD = 90 (gt)

Cạnh AD chung

∠BAD = ∠HAD (gt)

⇒ ΔABD = ΔAHD (ch - gn)

b)  Xét ΔABC có: 

∠B = 90^o 

⇒ ∠A + ∠C =90^o

⇒ ∠C = 90^o − ∠A = 90^o − 60^o = 30^o

Vì AD là tia phân giác của ∠A (gt)

⇒ ∠BAD = ∠DAC = ∠A/2 = 60^o/2 = 30^o

⇒ ∠C = ∠DAC = 30^o 

⇒ ΔADC cân tại D

⇒ AD = DC

⇒ AH = HC (quan hệ giữa đường xiên và hình chiếu)

c) Xét ΔABD có :

AB < AD (cạnh góc vuông < cạnh huyền)

Mà AD = DC (cmt) 

⇒ DC > AB

Hai ý còn lại bạn tự làm nhé mik mỏi tay lắm rùi