Cho hình chóp S ABCD . có đáy ABCD là hình vuông tâm O , cạnh bằng, 2a . SA vuông góc với mặt đáy và SA =a .
a) Chứng minh: BD vg (SAC) .
b) Gọi N là trung điểm của CD . Xác định và tính góc giữa đường thẳng SN với mặt phẳng (SBD).
Cho hình chóp S(ABCD) đáy là hình vuông cạnh a SA vuông góc (ABCD) SA= a√2 a, chứng minh BD vuông góc với (SAC) b, tính góc a giữa đường SC và mặt đáy
Ta có:
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
b.
Do \(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{a\sqrt{2}}{a\sqrt{2}}=1\)
\(\Rightarrow\widehat{SCA}=45^0\)
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).
b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.
c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α)
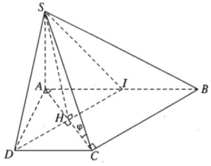
a) Ta có:
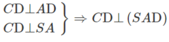
⇒ (SCD) ⊥ (SAD)
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
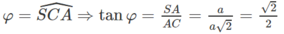
c) 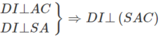
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và 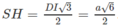 .
.
Tam giác SDI có diện tích:
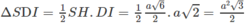
Câu 5: Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O cạnh bằng a, góc giữa cạnh bên và mặt đáy 1 góc 60°. Gọi IE lần lượt là là trung điểm của cạnh BC,CD a)Chứng minh: AC vuông góc (SBD) ; BD vuông góc SA b)Chứng minh: (SBC) vuông góc (SOI) c)Tính góc giữa mặt bên và mặt đáy. d)góc giữa OE và mặt (SCD) e)Tính khoảng cách giữa SI và AB.
a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, A B = B C = a , A D = 2 a , S A vuông góc với mặt đáy A B C D , S A = a . Gọi M, N lần lượt là trung điểm của SB, CD. Tính cosin của góc giữa MN và (SAC).
A. 2 5
B. 55 10
C. 3 5 10
D. 1 5
cho hình chóp SABCD đáy ABCD là hình chữ nhật AB= a ,AD=2a,SA=SB=SC=SD=2a gọi O là giao điểm của AC và BD
a chứng minh mặt phẳng SAC vuông góc với mặt phẳng ABCD
b tính khoảng cách từ O->mặt phẳng SCD
c gọi M,N lần lượt là trung điểm của các cạnh SA và BC tính sin góc MN,CSBD
Cho hình chóp S.ABCD có SA vuông góc với đáy và SA=a/2 . Đáy ABCD là hình vuông cạnh 2a. a, Xác định góc giữa (SBD) và (ABCD). b, Xác định góc giữa (SCD) và (SAC).
a: (SBD) giao (ABCD)=BD
AB vuông góc BD
SB vuông góc BD
=>góc cần tìm là góc SBA
Cho hình chóp S.ABCD có \(SA\perp\left(ABCD\right)\), đáy ABCD là hình vuông cạnh 2a, SA= \(2a\sqrt{3}\) .
1. Chứng minh \(\left(SAC\right)\perp\left(SBD\right)\)
2. Gọi I là trung điểm của AD, mặt phẳng (P) qua I và vuông góc với SD. Xác định và tính thiết diện của hình chóp cắt bởi mặt phẳng (P).
Help me!!!
1: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SAC) vuông góc (SBD)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc vs mặt đáy, SA=a căn 3. Gọi O là giao điểm của BD và AC 1. CMR: CD vuông góc ( SAD) 2. CMR: SO vuông góc BD 3.xác định và tính góc giữa SO và mp( ABCD)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(SO\in\left(SAC\right)\Rightarrow BD\perp SO\)
c.
\(SA\perp\left(ABCD\right)\Rightarrow AO\) là hình chiếu vuông góc của SO lên (ABCD)
\(\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
\(tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{6}\Rightarrow\widehat{SOA}\approx67^047'\)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại B. AB=BC=a, AD=2a. Biết SA vuông góc với đáy (ABCD) và SA=a. Gọi M,N lần lượt là trung điểm SB,CD. Tính sin góc giữa đường thẳng MN và mặt phẳng (SAC)
A. 5 5
B. 55 10
C. 3 5 10
D. 2 5 5