Giúp mình vs các bạn 


Những câu hỏi liên quan

các bạn giúp mình vs mình cần gấp ạ
Bài 1:
Phần a bạn tự làm nha! (Đ/S: 0,5)
b, B = \(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{\sqrt{x}+2}{3-\sqrt{x}}+\dfrac{\sqrt{x}+2}{x-5\sqrt{x}+6}\) với \(x\ge0;x\ne4;x\ne9\)
B = \(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
B = \(\dfrac{x-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{x-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
B = \(\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
B = \(\dfrac{1}{\sqrt{x}-2}=\dfrac{\sqrt{x}+2}{x-4}\)
Vậy ...
c, Ta có: A = \(1-\dfrac{\sqrt{x}}{\sqrt{x}+1}\)= \(\dfrac{1}{\sqrt{x}+1}\)
T = \(\dfrac{A}{B}\)= \(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)= 1 - \(\dfrac{3}{\sqrt{x}+1}\)
Ta có: x \(\ge\) 0 \(\Leftrightarrow\) \(\sqrt{x}\ge0\) \(\Leftrightarrow\) \(\sqrt{x}+1\ge1\) \(\Leftrightarrow\) \(\dfrac{3}{\sqrt{x}+1}\le3\) \(\Leftrightarrow\) \(-\dfrac{3}{\sqrt{x}+1}\ge-3\) \(\Leftrightarrow\) T \(\ge\) -2
Vậy ...
Bài 2: ĐK: x \(\ge\) 0
Giả sử: \(P\) < \(\sqrt{P}\)
\(\Leftrightarrow\) \(\dfrac{\sqrt{x}+2}{\sqrt{x}+5}< \dfrac{\sqrt{\sqrt{x}+2}}{\sqrt{\sqrt{x}+5}}\)
\(\Leftrightarrow\) \(\dfrac{\sqrt{\left(\sqrt{x}+2\right)\left(\sqrt{x}+5\right)}-\left(\sqrt{x}+2\right)}{\sqrt{x}+5}>0\)
\(\Leftrightarrow\) \(\sqrt{\left(\sqrt{x}+2\right)\left(\sqrt{x}+5\right)}-\left(\sqrt{x}+2\right)>0\) (\(\sqrt{x}+5>0\) với mọi x \(\ge\) 0)
\(\Leftrightarrow\) \(\sqrt{\left(\sqrt{x}+2\right)}\sqrt{\sqrt{x}+5-\sqrt{x}-2}>0\)
\(\Leftrightarrow\) \(\sqrt{\left(\sqrt{x}+2\right)}\sqrt{3}>0\)
\(\Leftrightarrow\) \(\sqrt{\sqrt{x}+2}>0\)
Vì x \(\ge\) 0 \(\Leftrightarrow\) \(\sqrt{x}+2\ge2\) \(\Leftrightarrow\) \(\sqrt{\sqrt{x}+2}\ge\sqrt{2}>0\) (Đpcm)
Vậy \(P\) < \(\sqrt{P}\)
Chúc bn học tốt!
Đúng 2
Bình luận (2)
Các bạn ơi giúp mình câu hỏi này vs nhé là ưu điểm và nhược điểm của kL và PKL mong các bạn giúp mình nhé
Các bạn giúp mình vs
ĐKXĐ : \(2-x^4\ge0\)
Áp dụng Cô si
\(\sqrt[4]{2-x^4}=\sqrt[4]{\left(2-x^4\right).1.1.1}\le\dfrac{2-x^4+1+1+1}{4}=\dfrac{5-x^4}{4}\)
\(VT\le\dfrac{x^2\left(5-x^4\right)}{4}-x^4+x^3-1=\dfrac{-\left(x-1\right)^2\left(\left(x^2+x\right)^2+6\left(x+\dfrac{2}{5}\right)^2\right)}{4}\le0=VP\)
Dấu "=" \(x=1\)
Vậy S = {1}
Đúng 1
Bình luận (2)
Khá căn bản ta dự đoán x=1.
`x^2\root{4}{2-x^4}-x^4+x^3-1=0`
`đk:-root{4}{2}<=x<root{4}{2}`
`<=>x^3-1+x^2\root{4}{2-x^4}-x^4=0`
`<=>(x-1)(x^2+x+1)+x^2(1-root{4}{2-x^4})=0`
`<=>(x-1)(x^2+x+1)+x^2((1-2+x^4)/(1+root{4}{2-x^4}))=0`
`<=>(x-1)(x^2+x+1)+(x^2(x-1)(x^3+x^2+x+1))/(1+root{4}{2-x^4})=0`
`<=>(x-1)(x^2+x+1+(x^2(x^3+x^2+x+1))/(1+root{4}{2-x^4}))=0`
`<=>x-1=0` do `x^2+x+1+(x^2(x^3+x^2+x+1))/(1+root{4}{2-x^4})>0`
`<=>x=1`
Đúng 1
Bình luận (1)
Các bạn giúp mình vs ah
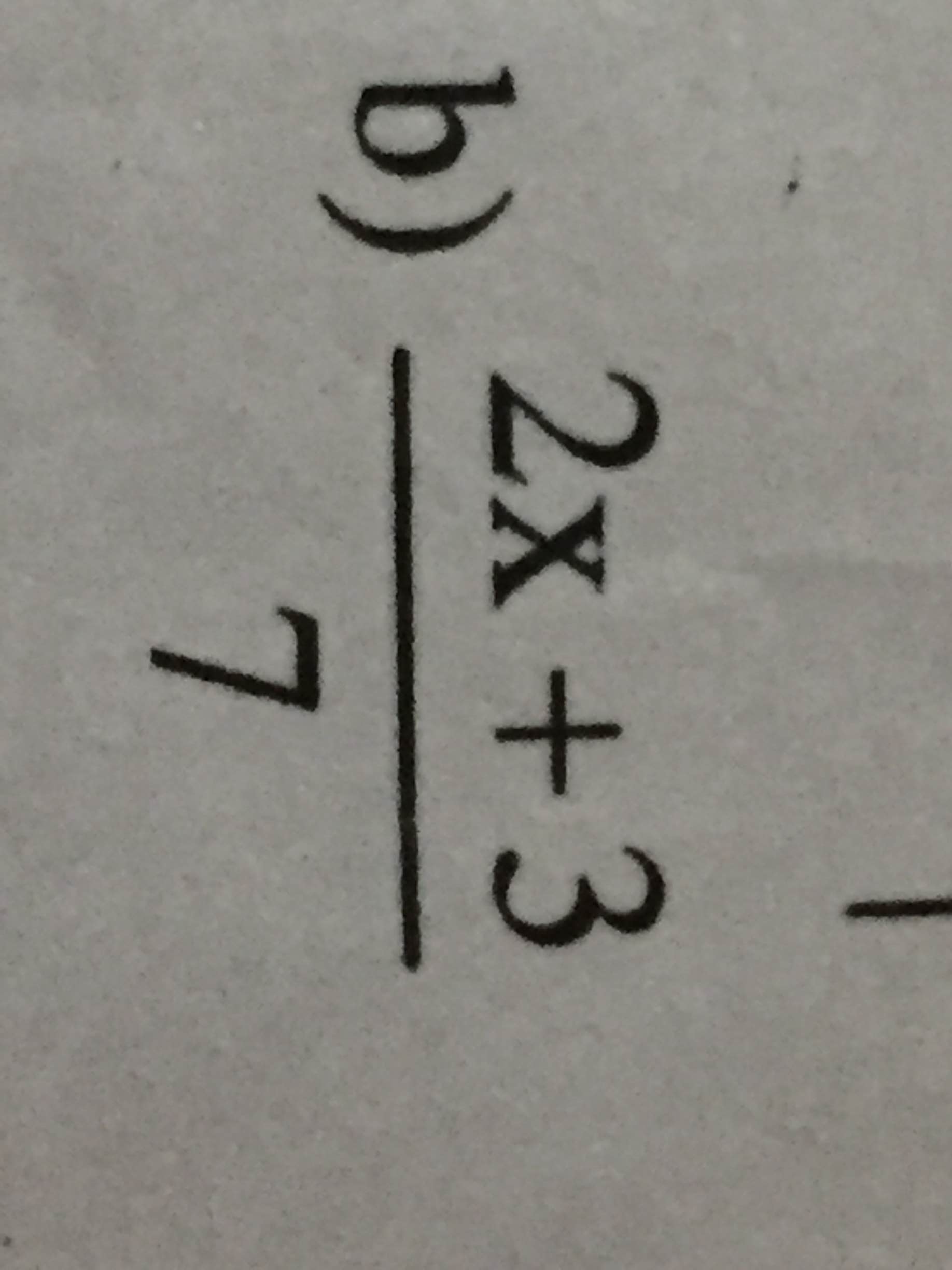

giúp mình vs. Thanks các bạn
Các bạn ơi giúp mình vs
Các bạn giải giúp mình vs
Giúp mình vs ạ mình cảm ơn các bạn nhìu lém 
12. In spite of feeling tired, the man tried to finish the work.
13.She swims very well.
Đúng 1
Bình luận (0)
CÁC BẠN GIÚP MÌNH VS Ạ MÌNH ĐANG CẦN GẤP Ạ
Đọc tiếp
CÁC BẠN GIÚP MÌNH VS Ạ MÌNH ĐANG CẦN GẤP Ạ




















