cho tam giác ABC vuông tại A có góc B = 60 độ Tia phân giác của góc B cắt AC tại E, kẻ EK vuông góc với BC (K ϵ BC)
a, Chứng minh ΔABE = ΔHBE
b, Chứng minh HB = HC
c, Từ H kẻ đường thẳng song song với BE cắt AC ở K. Chứng minh ΔEHK là tam giác đều
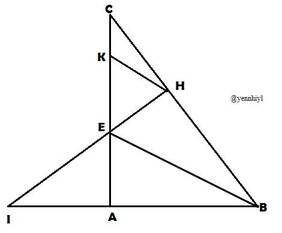
Cho tam giác ABC vuông ở A có góc B bằng 60 độ . Tia phân giác của góc ABC cắt AC ở E. Kẻ EH vuông góc với BC
a) Chứng minh tam giác ABE bằng tam giác HBE
b) Chứng minh HB = HC
c) Từ H kẻ đường thẳng song song với BE cắt AC ở K. Chứng minh tam giác EHK đều
d) Gọi I là giao điểm của BA và HE. Chứng minh IE > EH
a) Xét \(\Delta ABE\) và \(\Delta HBE\):
BE chung
\(\widehat{ABE}=\widehat{EBH}\)
\(\widehat{EAB}=\widehat{EHB}=90^o\)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) \(\widehat{EBH}=\dfrac{1}{2}\widehat{B}=30^o\)
\(\widehat{ACB}=90^o-\widehat{B}=30^o\)
\(\Rightarrow\Delta EBC\) cân tại E
Mà EH vuông góc BC
\(\Rightarrow HB=HC\)
c) \(\widehat{HEB}=90^o-\widehat{EBH}=60^o\)
\(KH//BE\Rightarrow\widehat{KHE}=\widehat{HEB}=60^o\)
\(\widehat{HEB}+\widehat{AEB}=60^o+60^o=120^o\)
\(\Rightarrow\widehat{KEH}=180^o-120^o=60^o\)
\(\Rightarrow\Delta EHK\) đều
d) Theo phần a. \(\Delta ABE=\Delta HBE\Rightarrow AE=EH\)
\(\Delta IAE\) vuông ở A \(\Rightarrow IE>AE\)
\(\Rightarrow IE>EH\)
a) Xét ΔABEΔABE và ΔHBEΔHBE:
BE chung
ˆABE=ˆEBHABE^=EBH^
ˆEAB=ˆEHB=90oEAB^=EHB^=90o
⇒ΔABE=ΔHBE(ch−gn)⇒ΔABE=ΔHBE(ch−gn)
b) ˆEBH=12ˆB=30oEBH^=12B^=30o
ˆACB=90o−ˆB=30oACB^=90o−B^=30o
⇒ΔEBC⇒ΔEBC cân tại E
Mà EH vuông góc BC
⇒HB=HC⇒HB=HC
c) ˆHEB=90o−ˆEBH=60oHEB^=90o−EBH^=60o
KH//BE⇒ˆKHE=ˆHEB=60oKH//BE⇒KHE^=HEB^=60o
ˆHEB+ˆAEB=60o+60o=120oHEB^+AEB^=60o+60o=120o
⇒ˆKEH=180o−120o=60o⇒KEH^=180o−120o=60o
⇒ΔEHK⇒ΔEHK đều
d) Theo phần a. ΔABE=ΔHBE⇒AE=EHΔABE=ΔHBE⇒AE=EH
ΔIAEΔIAE vuông ở A ⇒IE>AE
Cho tam giác ABC có AB lớn hơn AC tia phân giác của góc A cắt BC tại D qua B kẻ đường thẳng vuông góc với AC cắt AC tại E
a Chứng minh AB =AE
b qua qua e kẻ đường thẳng song song với BC cắt AD tại F kẻ đường hai đường thẳng song song với BC tại K
Gọi Bx là tia đối của tia BA. Lấy E trên AC sao cho AB = AE
Xét tam giác BAD=EAD c-g-c => BD = DE và DEC = CBx
Trong tam giác ABC, BAC + ABC + ACB = 180 => ACB = 180 - BAC - ABC => ACB < 180 - ABC
Ta có DBx + ABC = 180 (hai góc kề bù) => DBx = 180 - ABC
=>ACB < DBx => ACB < DEC => Trong tam giác DEC, DC > DE (Quan hệ giữa góc và cạnh)
Vậy BD < DC
Cho tam giác ABC vuông ở A có góc B bằng 60o. Tia phân giác của góc ABC cắt AC ở E. Kẻ EH vuông góc với BC ( HBC ).
a) Chứng minh ΔABE = ΔHBE
b) Chứng minh HB = HC
c) Từ H kẻ đường thẳng song song với BE cắt AC ở K. Chứng minh ΔEHK là tam giác đều.
d) Gọi I là giao điểm của BA và H
Bài 1 : Cho xOy có Oz là tia phân giác, M là điểm bất kì thuộc tia Oz. Qua M kẻ đường thẳng a vuông góc với Ox tại a cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B cắt tia Ox tại D. Chứng minh tam giác AOM bằng tam giác BOM ?
Bài 2 : Cho tam giác ABC có góc A = 90* và đường phân giác BH (H thuộc AC). Kẻ HM vuông góc với BC (M thuộc BC). Gọi N là giao điểm của AB và MH. Chứng minh tam giác ABH bằng tam giác MBH, tam giác ACE= tam giác AKE?
Bài 3: Cho tam giác ABC vuông tại C có góc A = 60* và đường phân gác của góc BAC cắt BC tại E. Kẻ EK vuông góc AB tại K (K thuộc AB). Kẻ BD vuông góc với AE tại D (D thuộc AE). Chứng minh tam giác ACE = tam giác AKE
Bài 4: Cho tam giác ABC vuông tại A có đường phân giác của góc ABC cắt AC tại E. Kẻ EH vuông góc BC tại H (H thuộc BC). Chứng minh tam giác ABE = tam giác HBE ?
Bài 1: tam giác ABC vuông góc tại C; góc A bằng 60'. Tia phân giác góc A cắt BC ở E. Kẻ EH vuông góc AB, kẻ BD vuông góc AE tại D
a) chứng minh AC=AH; AE vuông góc CH
b) chứng minh HA=HB
c) EB>AC
d) chứng minh 3 đường thẳng AC; BD; HE đồng quy
Bài 2: tam giác ABC; góc B bằng 60'. Vẽ p.giác BD. Từ A kẻ vuông góc với BD tại H và cắt BC tại E
a) tính số đo góc BAH và chứng minh tam giác ABE đều
b) chứng minh tam giác DBA= tam giác DBE
c) từ A kẻ song song BD cắt ĐC tại F. Chứng minh tam giác ABF cân
Cho tam giac ABC vuông tại A có góc C = 30 độ . Tia phân giác góc B cắt AC tại E . Từ E kẻ tia EH vuông góc với BC ( H thuộc BC )
a) So sánh các cạnh của tam giác ABC c) Chứng minh tam giác EAH cân
b) Chứng minh tam giác ABC = tam giác HBE d) Từ H kẻ HK song song với BE ( K thuộc AC ) . Chứng minh AE=EK=KC
https://lazi.vn/edu/exercise/cho-tam-giac-abc-vuong-tai-a-co-goc-c-30-do-tia-phan-giac-goc-b-cat-bc-tai-e-tu-e-ve-eh-vuong-goc-voi-bc
1. Cho tam giác ABC có AB = AC, góc BAC có số đo là 50 độ. Từ B kẻ BH vuông góc với AC tại H, từ C kẻ CK vuông góc với AB tại K.
a) Chứng minh: Tam giác ABH = tam giác ACK, BH = CK
b) Gọi O là giao điểm của BH và CK. Tính số đo của góc BOC
c) Cho M là trung điểm của BC. chứng minh BC = 2MK
2. Cho góc xOy bằng 60 độ; Oz là tia phân giác của góc xOy.Trên tia Ox lấy điểm A (A khác O); từ A kẻ đường thẳng vuông góc với Oz cắt Ox tại I và cắt Oy tại B, từ A kẻ đường thẳng song song với Oy cắt Oz tại C.
a)Chứng minh tam giác OAI = tam giác OBI và chứng minh tam giác OAB đều
b)Kẻ AH vuông góc với Oy tại H. Chứng minh AH = CI
c)Từ C kẻ đường thẳng song song với AB cắt Oy tại D. Chứng minh \(AD^2\)= \(3BD^2\)
Giúp mình với!
Đề bài: Cho △ABC cân tại A. Tia phân giác góc BAC cắt cạnh BC tại M.
a) Chứng minh: △AMB = △AMC
b) Kẻ ME vuông góc AB ( E ϵ AB ), MF vuông góc AC ( F ϵ AC ). Chứng minh △AEF cân
c) Chứng minh: AM vuông góc EF
d) Qua B kẻ đường thẳng song song với AC cắt đường thẳng FM tại I. Chứng minh: BE = BI
a) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\) (do \(\Delta ABC\) cân tại \(A\))
\(\widehat{BAM}=\widehat{CAM}\) (do \(AM\) là tia phân giác \(\widehat{A}\))
\(AM\) là cạnh chung
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.g.c\right)\)
b) Xét \(\Delta AEM\left(\widehat{AEM}=90^o\right)\) và \(\Delta AFM\left(\widehat{AFM}=90^o\right)\) có:
\(\widehat{EAM}=\widehat{FAM}\) (do \(AM\) là tia phân giác \(\widehat{A}\))
\(AM\) là cạnh chung
\(\Rightarrow\Delta AEM=\Delta AFM\left(ch.gn\right)\)
\(\Rightarrow AE=AF\) (\(2\) cạnh tương ứng)
\(\Rightarrow\Delta AEF\) cân tại \(A\)
c) Xét \(\Delta AEF\) cân tại \(A\) có \(AM\) là đường phân giác \(\widehat{A}\)
\(\Rightarrow AM\) cũng là đường trung trực \(\Delta AEF\)
\(\Rightarrow AM\perp EF\)
Tự vẽ hình
a, Tam giác AMB và tam giác AMC
AB = AC ( Tam giáC ABc cân )'
góc BAM = góc CAM ( AM là phân giác)
AM chung
=> Tam giác AMB = tam giác AMC ( c-g-c)
b, Xét tam giá AEM và tam giác AFM cs
góc AEM = góc AFM = 90 độ ( gt )
góc EAM = góc FAM ( AM là phân giác)
AM chung
=>tam giá AEM = tam giác AFM ( ch-gn)
=> AE = AF hay tam giác AEF cân tại A
c, Xét tam giác AEF cân tại A cs AM là tia phân giác đồng thời là đg cao
=> AM vuông góc vs EF
d, Tam giác ABC cân tại A
=> góc ABC = góc ACB
Ta có Tam giác ABC cân tại A
mà AM là tia phân giác đồng thời là trung tuyến
=> MB = MC
do BI // vs AC mà IE⊥ AC
=> BI ⊥ IE hay góc MIB = 90 độ
Xét tam giác MIB và tam giác MFC cs
góc F = góc M = 90 độ
MB = MC ( cmt)
góc BMI = góc FMC ( đối đỉnh)
=> tam giác MIB = tam giác MFC ( ch-gn)
=> góc MBI = góc MCF
mà góc MCF = góc ABC ( cmt)
=> góc MBI = góc ABC
Xét tam giác MEB và tam giác MIB cs
góc MBI = góc EBM(cmt)
góc E = góc M = 90 độ
BM chung
=> tam giác MEB = tam giác MIB ( ch-gn)
=> BE = BI
Cho tam giác ABC vuông tại A , BM là phân giác của góc B ( M thuộc AC ) . Từ M kẻ đường thẳng song song với AB cắt BC tại N
a, Chứng minh góc MBN = BMN
b, Từ N kẻ đường thẳng song song với BM cắt AC tại E . Chứng minh NE là phân giác của góc MNC
c, Giả sử góc ABC = 60 độ tính số đo góc NEC
Cho tam giác ABC vuông tại A . Tia phân giác góc B cắt AC tại D , tia phân giác góc C cắt AB tại E kẻ DH vuông góc với BC tại H, kẻ EK vuông góc với BC tại K a) Chứng minh BA=BH b) BD vuông góc với AH c) Chứng minh AB+AC=BC+HK d) Tính góc HAK
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
Suy ra: BA=BH
b: Ta có: ΔBAD=ΔBHD
nên DA=DH
hay D nằm trên đường trung trực của AH(1)
Ta có: BA=BH
nên B nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra BD là đường trung trực của AH
hay BD⊥AH
Mình chỉ làm câu c, d thôi nha ( vì câu a, b bạn Nguyễn Lê Phước Thịnh làm rồi)
c) Xét tam giác ECK và tam giác ECA có:
EKC=EAC=90
EC cạnh chung
ECK=ECA ( vì CE là p/g của ABC)
=>Tam giác ECK=Tam giác ECA ( ch-gn)
=>CK=CA( 2 cạnh tương ứng)
Mà AB=HB( chứng minh a)
=>CK+BH=CA+AB
=>CH+KH+BK+HK=AC+AB
=>(BK+KH+CH)+HK=AC+AB
=>BC+HK=AB+AC (ĐPCM)
d) Ta có: \(\left\{{}\begin{matrix}CK=CA\left(theo.c\right)\\BA=BH\left(theo.a\right)\end{matrix}\right.\)=>Tam giác ACK cân tại C và tam giác ABH cân tại B
=>\(\left\{{}\begin{matrix}CAK=CKA=\dfrac{180-ACB}{2}\\BAH=BHA=\dfrac{180-ABC}{2}\end{matrix}\right.\)
Có: BAH+CAK=BAK+HAK+HAC+HAK=BAK+2HAK+HAC=\(\dfrac{180-ABC}{2}+\dfrac{180-ACB}{2}\)=\(\dfrac{360-\left(ABC+ACB\right)}{2}\)
=\(\dfrac{360-90}{2}=135\)
=>BAK+2HAK+HAC=135
Mà BAK+HAC=BAC-HAK=90-HAK
=>90-HAK+2HAK=135
=>90+HAK=135
=>HAK=45