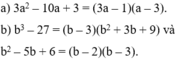Xét a=0=>10a+168=1+168=169=132

=> a=0;b=2

Xét a khác 0=>10a có tận cùng bằng 0 .

=> 10a+168 có tận cùng bằng 8 không phải số chính phương .

=> không có b

Vậy a=0; b=2

Bài 2 :

a) \(2^a+154=5^b\left(a;b\inℕ\right)\)

-Ta thấy,chữ số tận cùng của \(5^b\) luôn luôn là chữ số \(5\)

\(\Rightarrow2^a+154\) có chữ số tận cùng là \(5\)

\(\Rightarrow2^a\) có chữ số tận cùng là \(1\) (Vô lý, vì lũy thừa của 2 là số chẵn)

\(\Rightarrow\left(a;b\right)\in\varnothing\)

b) \(10^a+168=b^2\left(a;b\inℕ\right)\)

Ta thấy \(10^a\) có chữ số tận cùng là số \(0\)

\(\Rightarrow10^a+168\) có chữ số tận cùng là số \(8\)

mà \(b^2\) là số chính phương (không có chữ số tận cùng là \(8\))

\(\Rightarrow\left(a;b\right)\in\varnothing\)

Bài 3 :

a) \(M=19^k+5^k+1995^k+1996^k\left(với.k.chẵn\right)\)

Ta thấy :

\(5^k;1995^k\) có chữ số tận cùng là \(5\) (vì 2 số này có tận cùng là \(5\))

\(\Rightarrow5^k+1995^k\) có chữ số tận cùng là \(0\)

mà \(1996^k\) có chữ số tận cùng là \(6\) (ví số này có tận cùng là số \(6\))

\(\Rightarrow5^k+1995^k+1996^k\) có chữ số tận cùng là chữ số \(6\)

mà \(19^k\left(k.chẵn\right)\) có chữ số tận cùng là số \(1\)

\(\Rightarrow M=19^k+5^k+1995^k+1996^k\) có chữ số tận cùng là số \(7\)

\(\Rightarrow M\) không thể là số chính phương.

b) \(N=2004^{2004k}+2003\)

Ta thấy :

\(2004k=4.501k⋮4\)

mà \(2004\) có chữ số tận cùng là \(4\)

\(\Rightarrow2004^{2004k}\) có chữ số tận cùng là \(6\)

\(\Rightarrow N=2004^{2004k}+2003\) có chữ số tận cùng là \(9\)

\(\Rightarrow N\) có thể là số chính phương (nên câu này bạn xem lại đề bài)

Bài 4 :

a) \(5^5-5^4+5^3\)

\(=5^3.\left(5^2-5-1\right)\)

\(=5^3.19\) không chia hết cho 7 (bạn xem lại đề)

b) \(7^6+7^5-7^4\)

\(=7^4.\left(7^2+7-1\right)\)

\(=7^4.\left(49+7-1\right)\)

\(=7^4.55=7^4.11.5⋮11\)

\(\Rightarrow dpcm\)

c) \(1+2+2^2+2^3+...+2^{119}\)

\(=\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{117}\left(1+2+2^2\right)\)

\(=7+2^3.7+...+2^{117}.7\)

\(=7.\left(1+2^3+...+2^{117}\right)⋮7\)

\(\Rightarrow dpcm\)

e) \(3^{n+2}-2^{n+2}+3^n-2^n\)

\(=3^{n+2}+3^n-2^{n+2}-2^n\)

\(=3^n\left(3^2+1\right)-2^n\left(2^2+1\right)\)

\(=3^n.10-2^n.5\)

Ta thấy : \(3^n.10⋮10\)

Ta lại có : \(2^n\) có chữ số tận cùng là số chẵn

\(\Rightarrow2^n.5\) có chữ số tận cùng là số \(0\)

\(\Rightarrow2^n.5⋮10\)

Vậy \(3^n.10-2^n.5⋮10\left(dpcm\right)\)

Ta thấy 225 là số lẻ nên 100a + 3b + 1 và 2^a + 10a + b cũng là các số lẻ.

Do 100a + 3b + 1 là số lẻ mà 100a là số chẵn nên 3b là số chẵn tức b là só chẵn.

Kết hợp với 2^a + 10a + b là số lẻ ta có 2^a là số lẻ

\(\Leftrightarrow2^a=1\Leftrightarrow a=0\).

Khi đó: \(\left(3b+1\right)\left(b+1\right)=225\)

\(\Leftrightarrow\left(b-8\right)\left(3b+28\right)=0\Leftrightarrow b=8\) (Do b là số tự nhiên).

Vậy a = 0; b = 8.

?

\(A=2a^2+b^2-2ab+10a+42=\left(a^2-2ab+b^2\right)+\left(a^2+10a+25\right)+17=\left(a-b\right)^2+\left(a+5\right)^2+17\ge17\)

\(minA=17\Leftrightarrow a=b=-5\)

2) \(A=-x^2-y^2+2x-6y+9=-\left(x^2-2x+1\right)-\left(y^2+6y+9\right)+19=-\left(x-1\right)^2-\left(y+3\right)^2+19\)

\(maxA=19\Leftrightarrow\)\(\left\{{}\begin{matrix}x=1\\y=-3\end{matrix}\right.\)

C=2a²+b²-2ab+10a+42

=a²-2ab+b²+a²+10a+25+17

=(a-b)²+(a+5)²+17

=>MIN(C)=17 <=>a-b=0 và a+5=0

<=>a=b=-5

vậy ..................

10a + b = 7b

=> 10a = 7b - b

=> 10a = 6b

Cùng chia 2 vế cho 2 ta được:

5a = 3b

=> \(\frac{a}{b}=\frac{3}{5}\)

=> \(\frac{a}{b}=\frac{3k}{5k}\)

Nếu k > 2 

=> 5k > 10

=> b > 10 (vô lí)

=> k < 2

Nếu k = 0

=> 3k = 0

=> a = 0 (vô lí)

=> k > 0

=> 0< k < 2

=> k = 1

=> a = 1.3 = 3

=> b = 1.5 = 5

=> ab = 35

a chỉ có thể = 0,1,2,3,4,5,6,7,8,9

Thử :

100 : 7 = \(\frac{100}{7}\)( loại vì ko chia hết)

101 : 7 = \(\frac{101}{7}\)( loại )

102 : 7 = 102/7 ( loại )

103 : 7 = 103/7 ( loại )

104 : 7 = 104/7 ( loại )

105 : 7 = 15 ( nhận)

các số sau cũng chia ko hết.

Vậy a = 5 , b = 1 , c = 5

a có thể là 0,1,2,3,4,5,6,7,8,9

100:7= 100/7 ko chia hết

101:7=101/7 ko chia hết

102:7 =102/7 ko chia hết

103:7=103/7 ko chia hết

104:7 = 104/7 ko chia hết

105/7=15 chia hết cho 7

  vậy a = 5 , b=1 ,c=5