Giải bpt viết bảng xét dấu

Những câu hỏi liên quan
giải bpt băng cách lập bảng xét dấu:
\(\frac{x+2}{3x+1}\le\frac{x-2}{2x-1}\)

giải bpt bằng cách xét dấu
Giải bằng cách kẻ bảng xét dấu dùm em với ạ 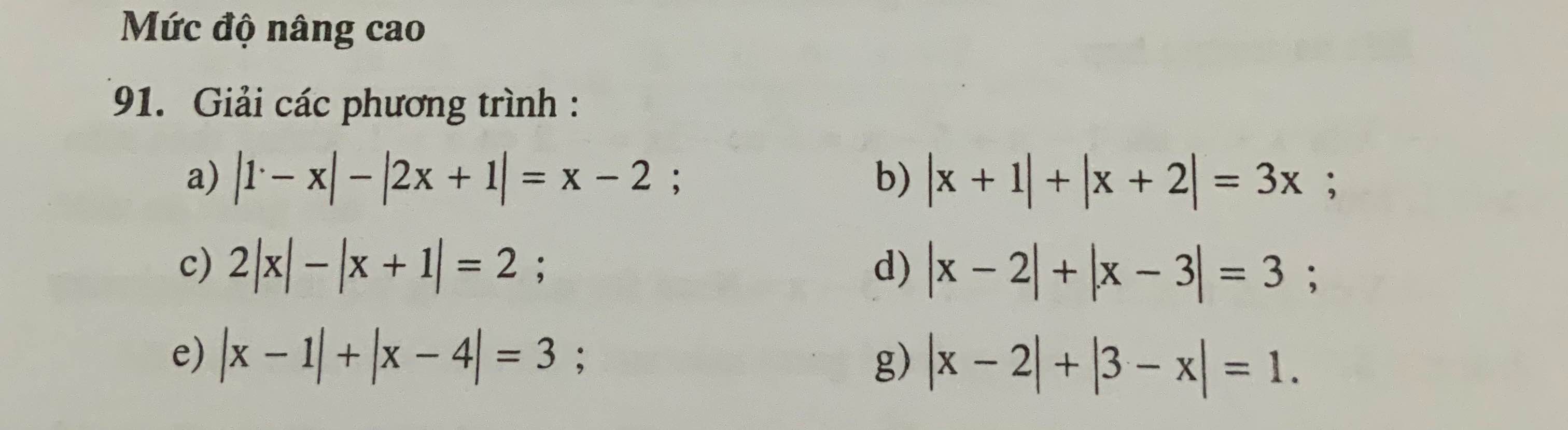
a: |1-x|-|2x+1|=x-2
=>|x-1|-|2x+1|=x-2(1)
TH1: x<-1/2
Phương trình (1) sẽ tương đương với:
1-x-(-2x-1)=x-2
=>1-x+2x+1=x-2
=>x+2=x-2
=>2=-2(vô lý)
=>\(x\in\varnothing\)
TH2: \(-\dfrac{1}{2}< =x< 1\)
Phương trình (1) sẽ trở thành:
\(1-x-\left(2x+1\right)=x-2\)
=>1-x-2x-1=x-2
=>-3x=x-2
=>-4x=-2
=>\(x=\dfrac{1}{2}\left(nhận\right)\)
TH3: x>=1
Phương trình (1) sẽ trở thành:
\(x-1-\left(2x+1\right)=x-2\)
=>x-1-2x-1=x-2
=>-x-2=x-2
=>-2x=0
=>x=0(loại)
b: \(\left|x+1\right|+\left|x+2\right|=3x\left(2\right)\)
TH1: x<-2
Phương trình (2) sẽ trở thành:
-x-1+(-x-2)=3x
=>\(3x=-2x-3\)
=>\(5x=-3\)
=>\(x=-\dfrac{3}{5}\left(loại\right)\)
TH2: -2<=x<-1
Phương trình (2) sẽ trở thành:
\(-x-1+x+2=3x\)
=>3x=1
=>\(x=\dfrac{1}{3}\left(loại\right)\)
TH3: x>=-1
Phương trình (2) sẽ trở thành:
\(x+1+x+2=3x\)
=>3x=2x+3
=>x=3(nhận)
c: \(2\left|x\right|-\left|x+1\right|=2\left(3\right)\)
TH1: x<-1
Phương trình (3) sẽ trở thành:
-2x-(-x-1)=2
=>-2x+x+1=2
=>-x+1=2
=>-x=1
=>x=-1(loại)
TH2: -1<=x<0
Phương trình (3) sẽ trở thành:
\(-2x-\left(x+1\right)=2\)
=>-2x-x-1=2
=>-3x=3
=>x=-1(nhận)
TH3: x>=0
Phương trình (3) sẽ trở thành:
\(2x-\left(x+1\right)=2\)
=>x-1=2
=>x=3(nhận)
d: \(\left|x-2\right|+\left|x-3\right|=3\left(4\right)\)
TH1: x<2
Phương trình (4) sẽ trở thành:
2-x+3-x=3
=>5-2x=3
=>2x=2
=>x=1(nhận)
Th2: 2<=x<3
Phương trình (4) sẽ trở thành:
\(x-2+3-x=3\)
=>1=3(loại)
Th3: x>=3
Phương trình (4) sẽ trở thành:
x-2+x-3=3
=>2x-5=3
=>2x=8
=>x=4(nhận)
e: |x-1|+|x-4|=3(5)
TH1: x<1
Phương trình (5) sẽ trở thành:
1-x+4-x=3
=>5-2x=3
=>2x=2
=>x=1(loại)
TH2: 1<=x<4
Phương trình (5) sẽ trở thành:
x-1+4-x=3
=>3=3(luôn đúng)
TH3: x>=4
Phương trình (5) sẽ trở thành:
x-1+x-4=3
=>2x-5=3
=>2x=8
=>x=4(nhận)
g: |x-2|+|3-x|=1
=>|x-2|+|x-3|=1(6)
TH1: x<2
Phương trình (6) sẽ trở thành:
2-x+3-x=1
=>5-2x=1
=>2x=4
=>x=2(loại)
TH2: 2<=x<3
Phương trình (6) sẽ trở thành:
x-2+3-x=1
=>1=1(luôn đúng)
TH3: x>=3
Phương trình (6) sẽ trở thành:
x-2+x-3=1
=>2x-5=1
=>2x=6
=>x=3(nhận)
Đúng 0
Bình luận (0)
Giải bất phương trình (x-1).(x+3) <0
**Lưu ý: làm cách thông thường, không phải lập bảng xét dấu các bạn nhé. Kết quả sau khi mình làm bằng cách lập bảng xét dấu là -3<x<1
Xe máy thứ nhất 1 giờ đi được 1/4 quảng đường
Xe máy thứ hai 1 giờ đi được 1/3 quảng đường
Sau 1,5 giờ 2 xe đi được:(1/4+1/3)x1,5=7/12x3/2=7/8(quảng đường)
quảng đường AB là:
15x8=120(km)
Đúng 0
Bình luận (0)
Xem lại đề đi bạnn
Trả lời đúng giúp mình.
Đúng 0
Bình luận (0)
giải hộ mk bằng bảng xét dấu cái dấu / này là giá trị tuyệt đối nhé /3x+2/+/2x-3/=4 /6-3x/+/2x+2/=14
mị nhìn thấy chữ nhưng hong bít câu trẻ lời
Đúng 1
Bình luận (0)
Em đổi lại môn câu hỏi để các bạn làm cho em nhé!
Đúng 1
Bình luận (0)
Cho bảng xét dấu:Bảng xét dấu trên là của tam thức bậc hai nào sau đây? A. f(x) -
x
2
- x + 6 B. f(x)
x
2
+ x - 6 C. f(x) -
x
2
+ x + 6 D. f(x)
x
2
- x + 6
Đọc tiếp
Cho bảng xét dấu:

Bảng xét dấu trên là của tam thức bậc hai nào sau đây?
A. f(x) = - x 2 - x + 6
B. f(x) = x 2 + x - 6
C. f(x) = - x 2 + x + 6
D. f(x) = x 2 - x + 6
Đáp án: A
Từ bảng xét dấu ta thấy phương trình f(x) = 0 có 2 nghiệm là -3 và 2. Do đó, ta loại được đáp án C và D
Dựa vào bảng xét dấu, f(x) > 0 trong khoảng (-3;2) do đó hệ số a < 0
Đúng 0
Bình luận (0)
Bài 1: giải phương trìnha,3sqrt{x-2}+sqrt{25x-50}2^5Bài 2: tìm giá trị của x và biểu diễn trên trục số thựca,x^2-5x+4 0 (đưa về BPT tích A.B 0xét A,B trái dấu)b,dfrac{x-3}{x+1} 1 (đưa về dạng dfrac{A}{B} 0.Xét left{{}begin{matrix}A,BBne0end{matrix}right.(a,b trái dấu)Bài 3: Để đi đoạn đường từ A đến B, một xe máy đã đi hết 3h20 phút, còn một ôtô chỉ đi 2h30 phút. Tính chiều dài quãng đường AB biết rằng vận tốc của ôtô lớn hơn vận tốc xe máy 20km/h.(bài này chỉ cần viết phương trình và giải phươn...
Đọc tiếp
Bài 1: giải phương trình
a,\(3\sqrt{x-2}+\sqrt{25x-50}=2^5\)
Bài 2: tìm giá trị của x và biểu diễn trên trục số thực
a,\(x^2-5x+4< 0\) (đưa về BPT tích A.B <0=>xét A,B trái dấu)
b,\(\dfrac{x-3}{x+1}< 1\) (đưa về dạng \(\dfrac{A}{B}\) <0.Xét \(\left\{{}\begin{matrix}A,B\\B\ne0\end{matrix}\right.\)(a,b trái dấu)
Bài 3: Để đi đoạn đường từ A đến B, một xe máy đã đi hết 3h20 phút, còn một ôtô chỉ đi 2h30 phút. Tính chiều dài quãng đường AB biết rằng vận tốc của ôtô lớn hơn vận tốc xe máy 20km/h.(bài này chỉ cần viết phương trình và giải phương trình)
AI LÀM ĐƯỢC CÁI NÀO THÌ LÀM,MK CẦN GẤP BÂY H,LÀM TỪ 3 CÂU TRỞ LÊN
Bài 2 :
a, Ta có : \(x^2-5x+4< 0\)
\(\Leftrightarrow x^2-x-4x+4< 0\)
\(\Leftrightarrow x\left(x-1\right)-4\left(x-1\right)< 0\)
\(\Leftrightarrow\left(x-4\right)\left(x-1\right)< 0\)
Vậy ...
b, Ta có : \(\dfrac{x-3}{x+1}< 1\)
\(\Leftrightarrow\dfrac{x-3}{x+1}-\dfrac{x+1}{x+1}< 0\)
\(\Leftrightarrow\dfrac{x-3-x-1}{x+1}=\dfrac{-4}{x+1}< 0\)
Thấy - 4 < 0
Nên để \(-\dfrac{4}{x+1}< 0\) <=> x + 1 > 0 ( TH A, B trái dấu )
Vậy ...
Đúng 2
Bình luận (1)
Bài 1:
a) ĐKXĐ: \(x\ge2\)
Ta có: \(3\sqrt{x-2}+\sqrt{25x-50}=2^5\)
\(\Leftrightarrow3\sqrt{x-2}+5\sqrt{x-2}=32\)
\(\Leftrightarrow8\sqrt{x-2}=32\)
\(\Leftrightarrow\sqrt{x-2}=4\)
\(\Leftrightarrow x-2=16\)
hay x=18(thỏa ĐK)
Vậy: S={18}
Đúng 1
Bình luận (0)
Lập bảng xét dấu để làm gì? Nêu ý nghĩa của bảng xét dấu trong phương trình chưa trị tuyệt đối
$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$
#$$%#^&*(*(*&$$#^&*((*&^&)*%#!@@%^^%
Xem thêm câu trả lời
Tìm x,biết:
/X-2/+/x-5/=3
Giải theo cách lập bảng xét dấu.
\(\left|x-2\right|+\left|x-5\right|=3\)
\(\Rightarrow x-2+x-5=3\)
\(\Rightarrow2x-7=3\)
\(\Rightarrow2x=10\)
\(\Rightarrow x=5\)
Đúng 0
Bình luận (0)
\(\left|x-2\right|+\left|x-5\right|=3\)
\(x-2+x-5=3\)
\(2x-7=3\)
\(5x=10\)
\(x=2\)
Đúng 0
Bình luận (0)



























