 làm hộ mik
làm hộ mik

Những câu hỏi liên quan

Bạn nào biết làm hộ mik được ko ạ! Mik cảm ơn! Bạn nào làm hộ mik, mik tick hết chứ ko phải mỗi bn đầu! Bạn nào biết bài nào thì làm hộ mik bài đó nha!
#include <bits/stdc++.h>
using namespace std;
double a,b,c,p,s;
int main()
{
cin>>a>>b>>c;
p=(a+b+c)/2;
s=sqrt(p*(p-a)*(p-b)*(p-c));
cout<<fixed<<setprecision(2)<<p;
return 0;
}
Đúng 0
Bình luận (0)
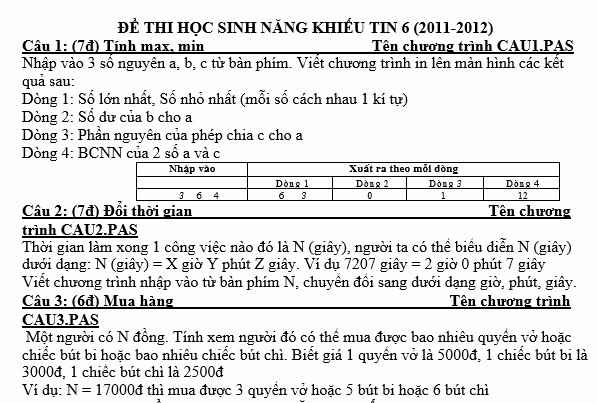
Bạn nào biết làm hộ mik được ko ạ! Mik cảm ơn! Bạn nào làm hộ mik, mik tick hết chứ ko phải mỗi bn đầu! Bạn nào biết bài nào thì làm hộ mik bài đó nha!
1:
uses crt;
var a,b,c,max,min:longint;
begin
clrscr;
readln(a,b,c);
max=a;
if max<b then max:=b;
if max<c then max:=c;
min:=a;
if min>c then min:=c;
if min>b then min:=b;
writeln(max,' ',min);
readln;
end.
Đúng 1
Bình luận (1)
làm hộ mik , mik cần gấp
Bài 1:
\(a)\left(x+\dfrac{2}{3}\right)^3=\dfrac{125}{64}.\\ \Leftrightarrow\left(x+\dfrac{2}{3}\right)^3=\left(\dfrac{5}{4}\right)^3.\\ \Rightarrow x+\dfrac{2}{3}=\dfrac{5}{4}.\\ \Leftrightarrow x=\dfrac{7}{12}.\)
\(b)\left(x-\dfrac{1}{2}\right)^3=\dfrac{8}{343}.\\\Leftrightarrow\left(x-\dfrac{1}{2}\right)^3=\left(\dfrac{2}{7}\right) ^3.\\ \Rightarrow x-\dfrac{1}{2}=\dfrac{2}{7}.\\ \Leftrightarrow x=\dfrac{11}{14}.\)
Bài 2:
\(a)\left(x-\dfrac{1}{3}\right)^2=\dfrac{25}{9}.\\ \Leftrightarrow\left[{}\begin{matrix}\left(x-\dfrac{1}{3}\right)^2=\left(\dfrac{5}{3}\right)^2.\\\left(x-\dfrac{1}{3}\right)^2=\left(\dfrac{-5}{3}\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{3}=\dfrac{5}{3}.\\x-\dfrac{1}{3}=\dfrac{-5}{3}.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2.\\x=\dfrac{-4}{3}.\end{matrix}\right.\)
\(b)\left(x-\dfrac{3}{4}\right)^2=\dfrac{49}{16}.\\ \Leftrightarrow\left[{}\begin{matrix}\left(x-\dfrac{3}{4}\right)^2=\left(\dfrac{7}{4}\right)^2.\\\left(x-\dfrac{3}{4}\right)^2=\left(\dfrac{-7}{4}\right)^2.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{3}{4}=\dfrac{7}{4}.\\x-\dfrac{3}{4}=\dfrac{-7}{4}.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}.\\x=-1.\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Làm hộ mik bài VIII. Mik cảm ơn!
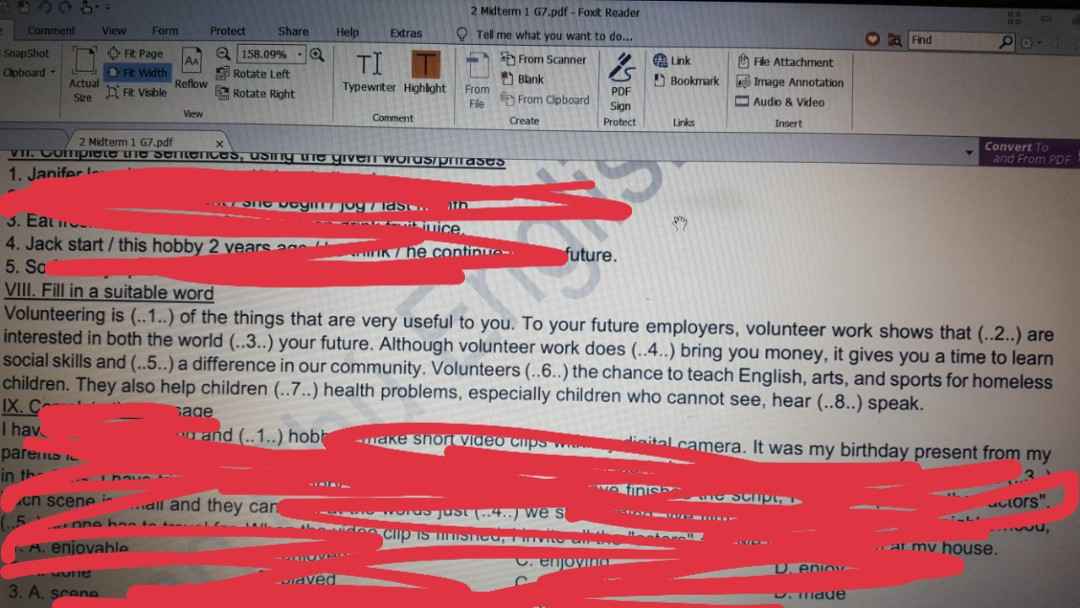
làm hộ mik bài nha!!!mik đang cần gấp!
làm nhanh hộ mik nha mik đang cần gấp
Đọc tiếp
làm nhanh hộ mik nha mik đang cần gấp\
Làm hộ mik bảng này ạ,mik cảm ơn
Làm hộ mik bài này ạ,mik cảm ơn
Lời giải:
a.
Nếu $m=3$ thì pt trở thành:
$x^2+4x-5=0$
$\Leftrightarrow (x-1)(x+5)=0$
$\Leftrightarrow x=1$ hoặc $x=-5$
b.
Để pt có 2 nghiệm pb $x_1,x_2$ thì:
$\Delta'=4+m^2-4>0\Leftrightarrow m^2>0\Leftrightarrow m\neq 0$
PT có 2 nghiệm $(-2+m, -2-m)$
Khi đó:
\(x_2=x_1^3+4x_2^2\Leftrightarrow \left[\begin{matrix} -2+m=(-2-m)^3+4(-2+m)^2\\ -2-m=(-2+m)^3+4(-2-m)^2\end{matrix}\right.\)
\(\Leftrightarrow \left[\begin{matrix} -m^3+2m^2-29m+10=0\\ m^3-2m^2+29m+10=0\end{matrix}\right.\)
Nghiệm khá xấu, cảm giác đề cứ sai sai bạn ạ.
Đúng 0
Bình luận (0)
làm hộ mik câu b,c mik cần gấp
a: Thay a=-2 vào pt, ta được:
\(-2x^2-2\cdot\left(-2-1\right)x-2+1=0\)
\(\Leftrightarrow-2x^2+6x-1=0\)
\(\Leftrightarrow2x^2-6x+1=0\)
\(\text{Δ}=\left(-6\right)^2-4\cdot2\cdot1=36-8=28>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{6-2\sqrt{7}}{2}=3-\sqrt{7}\\x_2=3+\sqrt{7}\end{matrix}\right.\)
b: Để phương trình có hai nghiệm phân biệt thì
\(\left\{{}\begin{matrix}\left(-2a+2\right)^2-4a\left(a+1\right)>0\\a< >0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^2-8a+4-4a^2-4a>0\\a< >0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-12a>-4\\a< >0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a< >0\\a< \dfrac{1}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)

làm hộ mik câu 3 ( mik đang cần gấp ạ )
\(A=\dfrac{2\sqrt{x}+17}{\sqrt{x+5}}=\dfrac{2\sqrt{x}+10}{\sqrt{x}+5}+\dfrac{7}{\sqrt{x}+5}=2+\dfrac{7}{\sqrt{x}+5}\)
Để \(A\) ∈ \(Z\) thì \(\dfrac{7}{\sqrt{x}+5}\) phải ∈ \(Z\)
=> \(\sqrt{x}+5\) ∈ \(Ư\left(7\right)=\left\{-7;-1;1;7\right\}\)
# Với \(\sqrt{x}+5=-7=>\sqrt{x}=-12\)(Loại)
#Với \(\sqrt{x}+5=-1=>\sqrt{x}=-6\)(Loại)
#Với \(\sqrt{x}+5=1=>\sqrt{x}=-4\left(Loại\right)\)
#Với \(\sqrt{x}+5=7=>\sqrt{x}=2< =>x=4\left(Nhận\right)\)
Vậy \(x=4\) thì \(A\)∈\(Z\)
Đúng 0
Bình luận (0)
\(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}3\)
\(Ta\) \(Có\) : \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}=\sqrt[3]{\dfrac{a^6}{ab.ab\left(a^2-ab+b^2\right)}}=\dfrac{a^2}{\sqrt[3]{ab.ab.\left(a^2-ab+b^2\right)}}\)
\(Áp\) \(dụng\) \(bđt\) \(AM-GM\)
\(\sqrt[3]{ab.ab\left(a^2-ab+b^2\right)}\text{≤}\) \(\dfrac{ab+ab+a^2-ab+b^2}{3}\)
\(=>\dfrac{a^2}{\sqrt[3]{ab.ab\left(a^2-ab+b^2\right)}}\) \(\text{≥}\) \(\dfrac{3a^2}{a^2+ab+b^2}\) \(Hay\) \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}\text{≥}\dfrac{3a^2}{a^2+ab+b^2}\)
Tương tự ta cũng có :
\(\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\text{≥}\dfrac{3b^2}{b^2+bc+c^2}\)
\(\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+a^2\right)}}\text{≥}\dfrac{3c^2}{a^2+ac+c^2}\)
\(=>\text{}\text{}\)\(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}\) \(3\left(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\right)\)
Cần c/m \(\left(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\right)\) ≥ \(1\)
Ta có : \(\dfrac{a^2}{a^2+ab+b^2}\text{≥}\dfrac{1}{3}\)
\(< =>3a^2\text{≥}a^2+ab+b^2\) \(< =>2a^2-b\left(a+b\right)\text{≥}0\) (1)
Lại có : \(a^2\text{≥}-b\left(a+b\right)\) (2)
Từ (1) và (2) => \(\dfrac{a^2}{a^2+ab+b^2}\text{≥}\dfrac{1}{3}\)
Tương tự ta cũng có :
\(\dfrac{b^2}{b^2+bc+c^2}\text{≥}\dfrac{1}{3}\)
\(\dfrac{c^2}{a^2+ac+c^2}\text{≥}\dfrac{1}{3}\)
Do đó \(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\text{≥}1\)
Suy ra : \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}\) \(3\)
Đẳng thức xảy ra <=> \(a=b=c=1\)
Đúng 0
Bình luận (0)

















