1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giải chi tiết giúp mik vs nhé 1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là h...
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
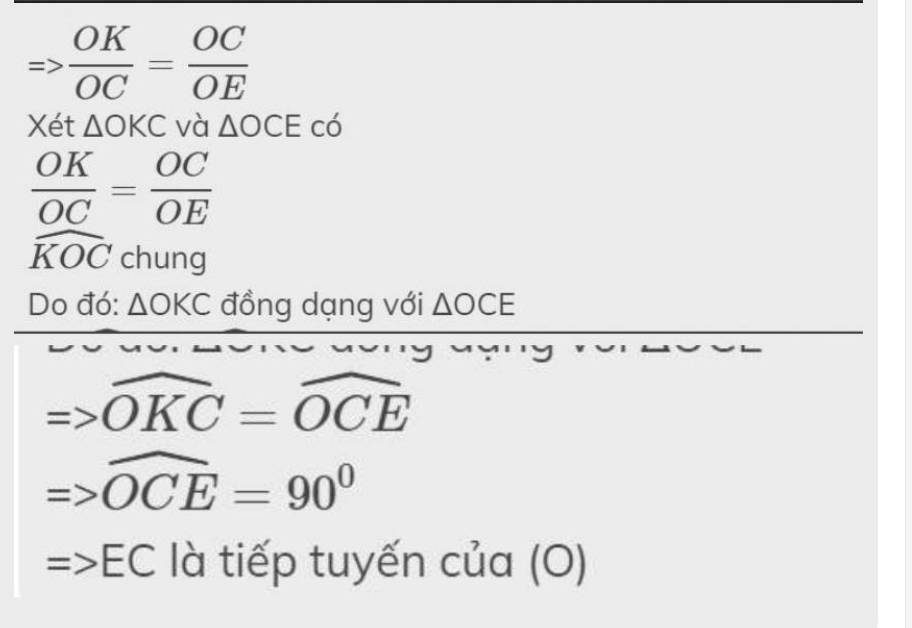
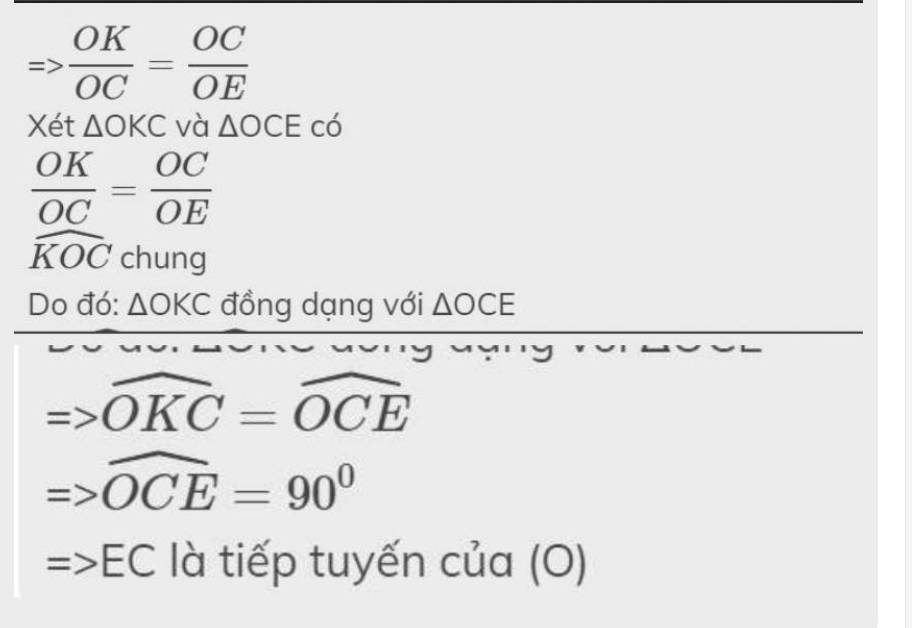
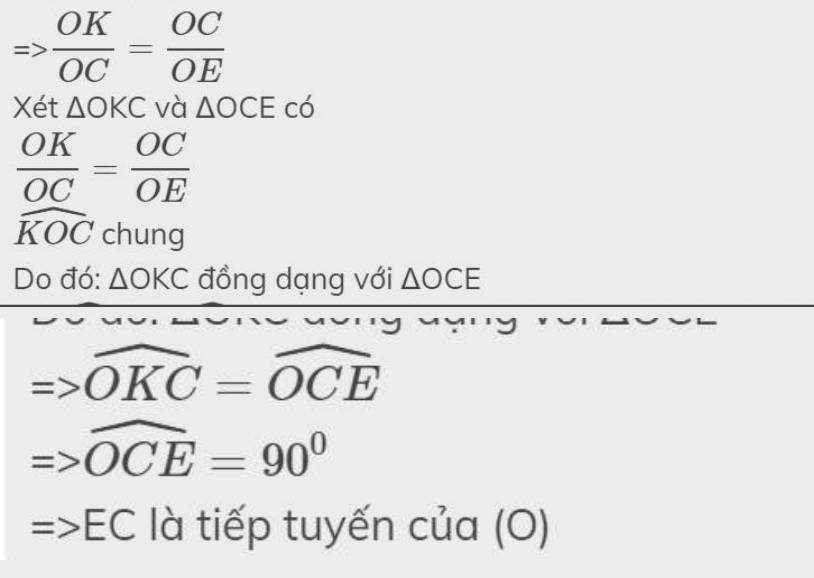
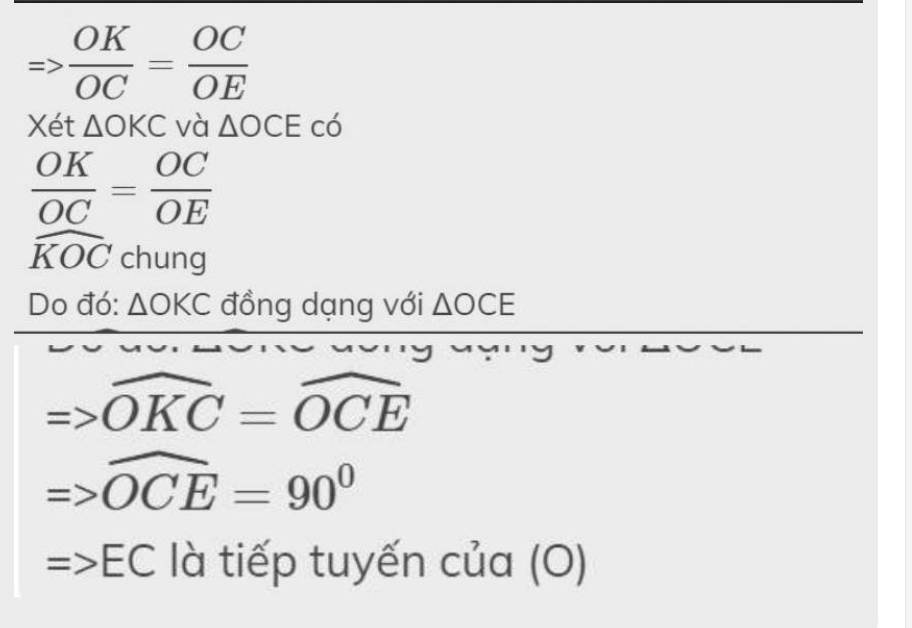
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé