Quy đồng mẫu thức \(\frac{3}{y-3};\frac{2y}{9-y^2}\)và \(\frac{y}{y+3}\)

Những câu hỏi liên quan
quy đồng mẫu thức
a)\(\frac{2x}{15x^3^{ }y^2}\)
\(\frac{-6y}{10x^4z^3^{ }}\)
quy đồng mẫu thức của các phân thức sau
\(x^2+1,\frac{x^4}{x^{2-1}}\)
\(\frac{x^3}{x^3-3x^2y+3xy^2-y^3},\frac{x}{y^2-xy}\)
Quy đồng mẫu thức hai phân thức \(\frac{1}{{3{{\rm{x}}^2} - 3}}\) và \(\frac{1}{{{x^3} - 1}}\)
Ta có:3x2 −3=3(x2−1)=3(x−1)(x+1)
x3 −1=(x−1)(x2 + x + 1)
MTC= 3(x−1)(x+1)(x2 + x + 1)
Nhân tử phụ của 3x2 − 3 là x2 + x + 1
Nhân tử phụ của x3 − 1 là 3(x+1)
Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng, ta có:
\(\frac{1}{{3{{\rm{x}}^2} - 3}} = \frac{{{x^2} + x + 1}}{{3\left( {{x^2} - 1} \right)\left( {{x^2} + x + 1} \right)}} = \frac{{{x^2} + x + 1}}{{3\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + x + 1} \right)}}\)
\(\frac{1}{{{x^3} - 1}} = \frac{{3\left( {x + 1} \right)}}{{3\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + x + 1} \right)}}\)
Đúng 0
Bình luận (0)
Quy đồng mẫu hai phân thức: \(\frac{1}{x};\frac{{ - 1}}{y}\)
Ta có : `1/x; -1/y`
\(\dfrac{1}{x}=\dfrac{1\cdot y}{x\cdot y}=\dfrac{y}{xy}\\ -\dfrac{1}{y}=\dfrac{-1\cdot x}{y\cdot x}=-\dfrac{x}{xy}\)
Đúng 1
Bình luận (0)
cho hai phân thức \(\frac{1}{x^2-4x-5}\) và \(\frac{2}{x^2+3x-10}\)
chứng tỏ rằng có thể chọn đa thức x3-7x2+7x+15 làm mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho.Hãy quy đồng mẫu thức
Cho hai phân thức: \(\frac{1}{x^2-4x-5}\) và \(\frac{2}{x^2-2x-3}\)
Chứng tỏ rằng có thể chọn đa thức \(x^3-7x^2+7x+15\)làm mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho. Hãy quy đồng mẫu thức
Quy đồng mẫu thức hai phân thức: \frac{5}{3z^{3}x}3z3x5 và \frac{1}{2x^{3}}2x31.
có ai giúp minh vs nhanh lên nha
Quy đồng mẫu thức các phân thức sau:
a) \(\frac{1}{{x + 2}};\frac{{x + 1}}{{{x^2} - 4{\rm{x}} + 4}};\frac{5}{{2 - x}}\)
b) \(\frac{1}{{3{\rm{x}} + 3y}};\frac{{2{\rm{x}}}}{{{x^2} - {y^2}}};\frac{{{x^2} - xy + {y^2}}}{{{x^2} - 2{\rm{x}}y + {y^2}}}\)
a) Ta có: \(\frac{5}{{2 - x}} = \frac{{ - 5}}{{x - 2}}\)
\({x^2} - 4{\rm{x}} + 4 = {\left( {x - 2} \right)^2}\)
\(MTC = \left( {x + 2} \right){\left( {x - 2} \right)^2}\)
Nhân tử phụ của x+2 là \({\left( {x - 2} \right)^2}\)
Nhân tử phụ của\({x^2} - 4{\rm{x}} + 4\) là \({\left( {x - 2} \right)^2}\)
Nhân tử phụ của x - 2 là (x+2)(x−2)
Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng, ta có:
\(\begin{array}{l}\frac{1}{{x + 2}} = \frac{{{{\left( {x - 2} \right)}^2}}}{{\left( {x + 2} \right){{\left( {x - 2} \right)}^2}}}\\\frac{{x + 1}}{{{x^2} - 4{\rm{x - 4}}}} = \frac{{\left( {x + 1} \right)\left( {x + 2} \right)}}{{\left( {x + 2} \right){{\left( {x - 2} \right)}^2}}}\\\frac{5}{{2 - x}} = \frac{{ - 5\left( {x + 2} \right)\left( {x - 2} \right)}}{{\left( {x + 2} \right){{\left( {x - 2} \right)}^2}}}\end{array}\)
b) Ta có: 3x+3y=3(x+y)
\({x^2} - {y^2} = \left( {x - y} \right)\left( {x + y} \right)\)
\({x^2} + 2{\rm{x}}y + {y^2} = {\left( {x - y} \right)^2}\)
\(MTC = 3\left( {x + y} \right){\left( {x - y} \right)^2}\)
Nhân tử phụ của 3x+3y là: \({\left( {x - y} \right)^2}\)
Nhân tử phụ của \({x^2} - {y^2}\) là: 3(x−y)
Nhân tử phụ của \({x^2} + 2{\rm{x}}y + {y^2}\) là: 3(x+y)
Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng, ta có:
\(\begin{array}{l}\frac{1}{{3{\rm{x}} + 3y}} = \frac{{{{\left( {x - y} \right)}^2}}}{{3\left( {x + y} \right){{\left( {x - y} \right)}^2}}}\\\frac{{2{\rm{x}}}}{{{x^2} - {y^2}}} = \frac{{6{\rm{x}}\left( {x - y} \right)}}{{3\left( {x + y} \right){{\left( {x - y} \right)}^2}}}\\\frac{{{x^2} - xy + {y^2}}}{{{x^2} - 2{\rm{x}}y + {y^2}}} = \frac{{3\left( {{x^2} - xy + {y^2}} \right)\left( {x + y} \right)}}{{3\left( {x + y} \right){{\left( {x - y} \right)}^2}}}\end{array}\)
Đúng 0
Bình luận (0)
Cho hai phân thức
1
x
2
-
4
x
-
5
;
2
x
2
-
2
x
-
3
Chứng tỏ rằng có thể chọn đa thức
x
3...
Đọc tiếp
Cho hai phân thức 1 x 2 - 4 x - 5 ; 2 x 2 - 2 x - 3 Chứng tỏ rằng có thể chọn đa thức x 3 - 7 x 2 + 7 x + 15 làm mẫu thức chung để quy đồng mẫu thức của hai phân thức đã cho. Hãy quy đồng mẫu thức.
Ta có:
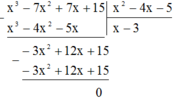
Suy ra: x 3 - 7 x 2 + 7 x + 15 = x 2 - 4 x - 5 x - 3
Lại có:
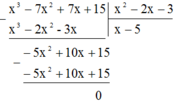
Suy ra: x 3 - 7 x 2 + 7 x + 15 = x 2 - 2 x - 3 x - 5
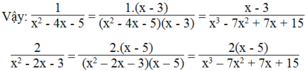
Đúng 0
Bình luận (0)












