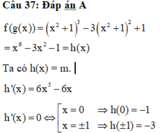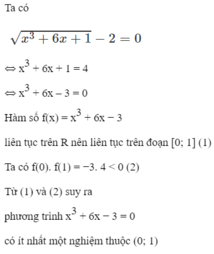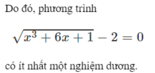Chứng minh rằng phương trình x3 -3x2-1=0 có nghiệm x thuộc (3,4) và x > 1+\(\sqrt[5]{36}\)

Những câu hỏi liên quan
Chứng minh rằng phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 thỏa mãn 0 < x 0 < 1 2
- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].

- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
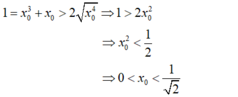
Đúng 0
Bình luận (0)
Cho hàm số f(x)x3−3x2+1�(�)�3−3�2+1.LG aXác định điểm I� thuộc đồ thị (C)(�) của hàm số đã cho biết rằng hoành độ của điểm I� là nghiệm của phương trình f′′(x)0�″(�)0.
Đọc tiếp
Cho hàm số .
LG a
Xác định điểm thuộc đồ thị của hàm số đã cho biết rằng hoành độ của điểm là nghiệm của phương trình .
\(f'\left(x\right)=3x^2-6x\Rightarrow f''\left(x\right)=6x-6\)
Theo đề: \(f''\left(x\right)=0\Leftrightarrow6x-6=0\Leftrightarrow x=1\).
Thay \(x=1\) vào \(f\left(x\right)\) \(\Rightarrow f\left(x\right)=-1\).
Vậy: Tọa độ điểm là \(I\left(1;-1\right)\)
Đúng 0
Bình luận (0)
Biết rằng đa thức P(x)=x3+3x2-1 có 3 nghiệm phân biệt. Chứng minh rằng trong 3 nghiệm đó tồn tại hai nghiệm a,b mà ab+a+1=0.
- Dễ dàng nhận thấy \(x=-1\) không phải là 1 nghiệm của đa thức P(x).
- Gọi b là 1 nghiệm của đa thức \(P\left(x\right)=x^3+3x^2-1\)
Do đó: \(b^3+3b^2-1=0\)
\(\Rightarrow\left(b^3+3b^2+3b+1\right)-3\left(b+1\right)+1=0\)
\(\Rightarrow\left(b+1\right)^3-3\left(b+1\right)+1=0\)
\(\Rightarrow\dfrac{\left(b+1\right)^3-3\left(b+1\right)+1}{\left(b+1\right)^3}=0\)
\(\Rightarrow\left(\dfrac{1}{b+1}\right)^3-3.\left(\dfrac{1}{b+1}\right)^2+1=0\)
\(\Rightarrow\left(-\dfrac{1}{b+1}\right)^3+3.\left(-\dfrac{1}{b+1}\right)^2-1=0\)
Thay \(x=-\dfrac{1}{b+1}\) vào \(P\left(x\right)=x^3+3x^2-1\) ta được:
\(P\left(-\dfrac{1}{b+1}\right)=\left(-\dfrac{1}{b+1}\right)^3+3.\left(-\dfrac{1}{b+1}\right)^2-1=0\)
\(\Rightarrow-\dfrac{1}{b+1}\) là một nghiệm của đa thức P(x).
Đặt \(a=-\dfrac{1}{b+1}\Rightarrow ab+a+1=0\) \(\Rightarrowđpcm\)
Đúng 4
Bình luận (0)
Cho hàm số
f
(
x
)
x
3
-
3
x
2
+
5
x
+
1
Hàm số yg(x) có bảng biến thiên như sauBiết rằng
a
,
b
∈
R
và ab;g(a).g(b)0 Phương trình g(f(x))0 có tất cả bao nhiêu nghiệm thực? A. 3 B. 9 C. 5 D. 1
Đọc tiếp
Cho hàm số f ( x ) = x 3 - 3 x 2 + 5 x + 1 Hàm số y=g(x) có bảng biến thiên như sau
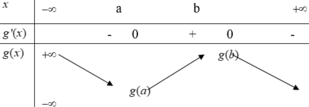
Biết rằng a , b ∈ R và a<b;g(a).g(b)<0 Phương trình g(f(x))=0 có tất cả bao nhiêu nghiệm thực?
A. 3
B. 9
C. 5
D. 1
Vì 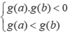
![]() Do đó đường thẳng y = 0 cắt đồ thị hàm số g(x) tại ba điểm phân biệt có hoành độ
Do đó đường thẳng y = 0 cắt đồ thị hàm số g(x) tại ba điểm phân biệt có hoành độ ![]() Vì vậy g(f(x)0
Vì vậy g(f(x)0 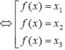
Hàm số f(x) có ![]() đồng biến trên R do đó mỗi phương trình
đồng biến trên R do đó mỗi phương trình ![]() có một nghiệm thực duy nhất.
có một nghiệm thực duy nhất.
Vậy phương trình đã cho có 3 nghiệm thực.
Chọn đáp án A.
Đúng 0
Bình luận (0)
Cho hàm số
g
(
x
)
x
2
+
1
và hàm số
f
(
x
)
x
3
-
3
x
2
+
1
. Tìm m để phương trình
f
(
g
(
x
)
)
-
m
0
có 4 nghiệm phân biệt. A.
-...
Đọc tiếp
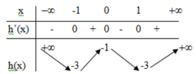
Cho hàm số g ( x ) = x 2 + 1 và hàm số f ( x ) = x 3 - 3 x 2 + 1 . Tìm m để phương trình f ( g ( x ) ) - m = 0 có 4 nghiệm phân biệt.
A. - 3 < m < 1
B. - 3 < m ≤ 1
C. - 3 ≤ m ≤ - 1
D. m > - 1
Cho phương trình: x2 - 2(m+1)x +m-4=0
a/ giải phương trình khi m=5
b/ chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi m
c/ tìm m để phương trình có hai nghiệm trái dấu
d/ chứng minh rằng biểu thức M= x1(1-x2) + x2 (1-x1) không phụ thuộc vào m
Xin lựa a;b ... c;d e rỗng tuếch :>> (ko bt đúng ko nữa).
a, Thay m = 5 vào biểu thức ta đc
\(x^2-2\left(5+6\right)x+5-4=0\)
\(x^2-33x+1=0\)
\(\Delta=\left(-33\right)^2-4.1.1=1089-4=1085>0\)
Nên phương trình có 2 nghiệm phân biệt
\(x_1=\frac{33-\sqrt{1085}}{2};x_2=\frac{33+\sqrt{1085}}{2}\)
b, Ta có :
\(\Delta=\left(2m-2\right)^2-4\left(m-4\right)=4m^2-4-4m+16=4m^2-4m+12\)
\(=\left(4m^2-4m+1\right)+11\ge11\forall m\)
Vậy phuwong trình có 2 nghiệm phân biệt vs mọi x
Câu 1: Cho hai đa thức bậc ba:
P(x)=x3+2x2−7x−16, Q(x)=x3+3x2+8x−4
a) Chứng minh rằng mỗi đa thức đều có một nghiệm dương duy nhất
b) Gọi các nghiệm dương của P(x),Q(x) lần lượt là p,q. Chứng minh rằng: sqrtp−sqrtq=1
Chứng minh rằng phương trình x 3 + 6 x + 1 - 2 = 0 có nghiệm dương
Cho phương trình x2+ 2(m − 1)x − 6m − 7 = 0 (1) (m là tham số).
a) Chứng minh rằng với mọi giá trị của m thì phương trình (1) luôn có hai nghiệm phân biệt.
b) Gọi x1, x2là hai nghiệm của phương trình (1). Tìm các giá trị của m thỏa x1(x1+3/3x2)+x2(x2+3/2x1)=15
các bạn ai biết thì chỉ giúp mình với ạ
\(x^{2^{ }}+2\left(m-1\right)x-6m-7=0\left(1\right)\)
a) \(Dental=\left[2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-6m-7\right)\)
\(< =>4\cdot\left(m^2-2m+1\right)+24m+28\)
\(< =>4m^2-8m+4+24m+28\)
\(< =>4m^2+16m+32\)
\(< =>\left(2m+4\right)^2+16>0\) với mọi m
Vậy phương (1) luôn có 2 nghiệm phân biệt với mọi m
b) Theo định lí vi ét ta có:
x1+x2= \(\dfrac{-2\left(m-1\right)}{1}=-2m+1\)
x1x2= \(-6m-7\)
Đúng 0
Bình luận (0)
quy đồng
khử mẫu
tách sao cho có tích và tổng
thay x1x2 x1+x2
kết luận
mặt xấu vl . . .![]()
Đúng 0
Bình luận (0)