Chứng tỏ A <2014 biết A = 2013+1/16+1/25+1/36+......+1/100+1/121.
Làm cụ thể mới tick nha.
Cho A =2+2^2+2^3+2^4+...+2^120 :
a , Tính A
b, So sánh A với 8^41
c, Chứng tỏ A+2 là lũy thừa của 2
d, Chứng tỏ A chia hết cho 3
e, Chứng tỏ A chia hết cho 7
g, Chứng tỏ A chia hết cho 15
h, Chứng tỏ 6 là ước của A
i, Chừng tỏ A là bội của 31
k, Chứng tỏ A là bội của 30
a) Cho P = 1 + 3 + 32 + 33 +.......+ 3101. Chứng tỏ rằng P⋮13.
b) Cho B = 1 + 22 + 24 +.......+ 22020. Chứng tỏ rằng B ⋮ 21.
c) Cho A = 2 + 22 + 23 +........+ 220. Chứng tỏ A chia hết cho 5.
d) Cho A = 1 + 4 + 42 + 43 +..........+ 498. Chứng tỏ A chia hết cho 21.
e) Cho A = 119 + 118 + 117 +.........+ 11 + 1. Chứng tỏ A chia hết cho 5.
a) P = 1 + 3 + 3² + ... + 3¹⁰¹
= (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)
= 13 + 3³.(1 + 3 + 3²) + ... + 3⁹⁹.(1 + 3 + 3²)
= 13 + 3³.13 + ... + 3⁹⁹.13
= 13.(1 + 3³ + ... + 3⁹⁹) ⋮ 13
Vậy P ⋮ 13
b) B = 1 + 2² + 2⁴ + ... + 2²⁰²⁰
= (1 + 2² + 2⁴) + (2⁶ + 2⁸ + 2¹⁰) + ... + (2²⁰¹⁶ + 2²⁰¹⁸ + 2²⁰²⁰)
= 21 + 2⁶.(1 + 2² + 2⁴) + ... + 2²⁰¹⁶.(1 + 2² + 2⁴)
= 21 + 2⁶.21 + ... + 2²⁰¹⁶.21
= 21.(1 + 2⁶ + ... + 2²⁰¹⁶) ⋮ 21
Vậy B ⋮ 21
c) A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... + 2¹⁶) ⋮ 5
Vậy A ⋮ 5
d) A = 1 + 4 + 4² + ... + 4⁹⁸
= (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + ... + (4⁹⁷ + 4⁹⁸ + 4⁹⁹)
= 21 + 4³.(1 + 4 + 4²) + ... + 4⁹⁷.(1 + 4 + 4²)
= 21 + 4³.21 + ... + 4⁹⁷.21
= 21.(1 + 4³ + ... + 4⁹⁷) ⋮ 21
Vậy A ⋮ 21
e) A = 11⁹ + 11⁸ + 11⁷ + ... + 11 + 1
= (11⁹ + 11⁸ + 11⁷ + 11⁶ + 11⁵) + (11⁴ + 11³ + 11² + 11 + 1)
= 11⁵.(11⁴ + 11³ + 11² + 11 + 1) + 16105
= 11⁵.16105 + 16105
= 16105.(11⁵ + 1)
= 5.3221.(11⁵ + 1) ⋮ 5
Vậy A ⋮ 5
A = 3 + 3^2+ 3^3 + 3^3 + ... + 3^132
a, chứng tỏ A chia hết cho 40
b, chứng tỏ A chia hết cho 39
c, chứng tỏ A chia hết cho 120
a: A=3(1+3+3^2+3^3)+...+3^129(1+3+3^2+3^3)
=40(3+...+3^129) chia hết cho 40
b: A=(3+3^2+3^3)+....+3^129(3+3^2+3^3)
=39(1+...+3^129) chia hết cho 39
c: A chia hết cho 40
A chia hết cho 3
=>A chia hết cho BCNN(40;3)=120
MN ơi giải giúp em bài này với : a) chứng tỏ tia A3=B1 b) chứng tỏ A3 + B4= 180 độ c) chứng tỏ A1=B1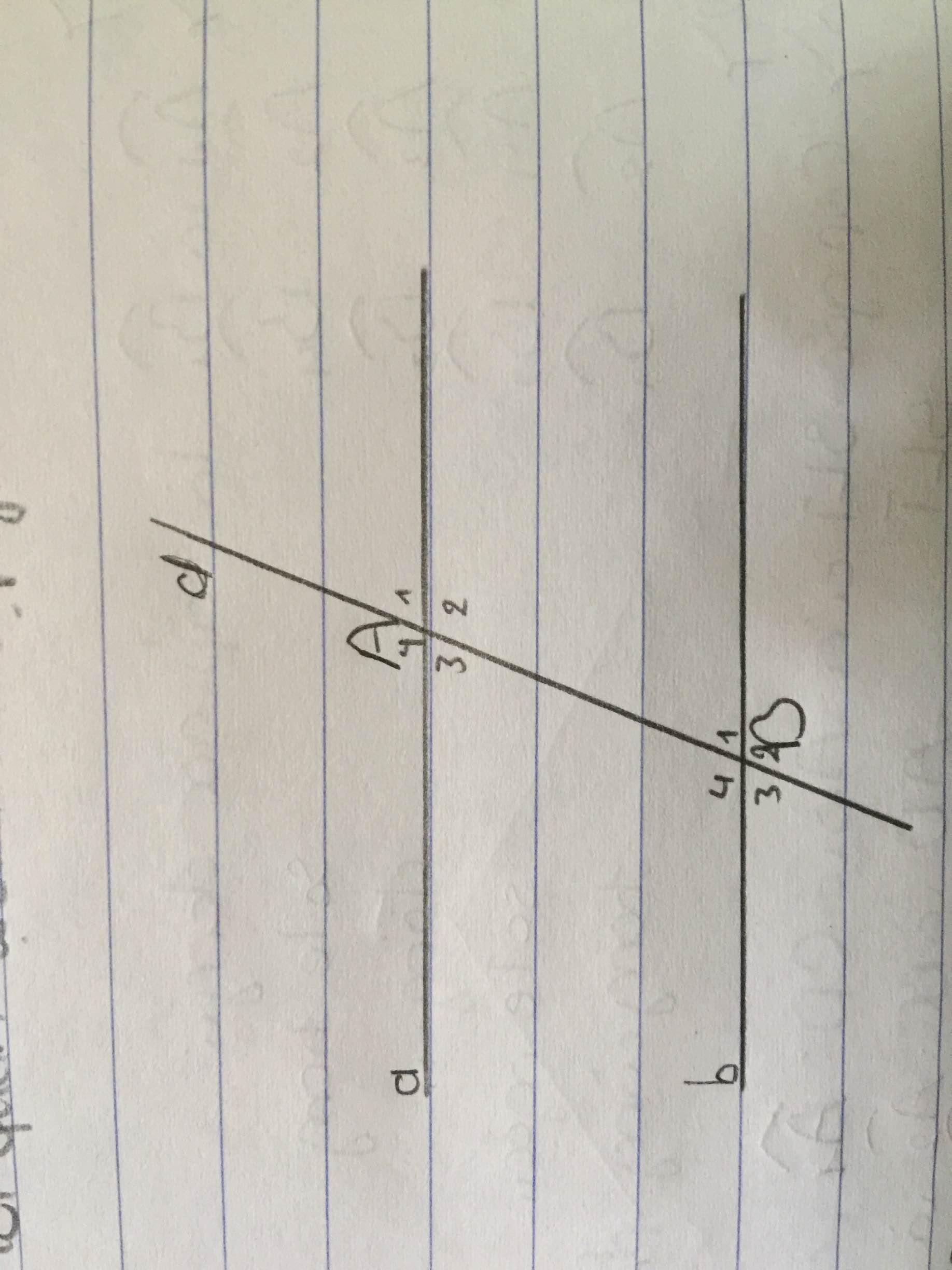
a)A3=B1 vì // ( sole trong = nhau) nhớ tick nhé
b) vì // (trong cùng phía bù nhau)
nhớ tick nhé
a) Cho A = 1 + 3 + 32 + 33 +..+ 399. Chứng tỏ rằng A ⋮ 9
b) Cho A = 5 + 52 + 53 + .....+ 540. Chứng tỏ rằng A ⋮ 2;3
Lời giải:
a. Ta thấy:
$3+3^2+3^3+...+3^{99}\vdots 3$
$1\not\vdots 3$
$\Rightarrow A=1+3+3^2+...+3^{99}\not\vdots 3$
$\Rightarrow A\not\vdots 9$
b.
$A=(5+5^2)+(5^3+5^4)+...+(5^{39}+5^{40})$
$=5(1+5)+5^3(1+5)+...+5^{39}(1+5)$
$=5.6+5^3.6+....+5^{39}.6$
$=6(5+5^3+...+5^{39})$
$=2.3.(5+5^3+...+5^{39})$
$\Rightarrow A\vdots 2$ và $A\vdots 3$
các bạn ơi giúp mik vs !!!!!!!!!!!!!!
Cho 4 số a,b,c,d. Khi chia cho 7 thì số dư lần lượt là 6,4,3,2:
Chứng tỏ b+ c chia hết cho 7
Chúng tỏ a+b-c chia hết cho 7
Chứng tỏ a-b-c chia hết cho 7
Chứng tỏ a+2.d chia hết cho 7
Chứng tỏ a+b+c+d chia 7 dư 1
a, b : 7 dư 4 ; c chia 7 dư 3 mà 4 + 3 = 7 chia hết cho 7
=> b+c chia hết cho 7
b, ( tương tự dựa vào đó mà lm nhé mày ) biết chưa quỷ cái
\(a,\widehat{N_1}++\widehat{N_4}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{N_1}=180^0-105^0=75^0\\ \Rightarrow\widehat{N_1}=\widehat{M_1}\)
Mà 2 góc này ở vị trí so le trong nên \(a//b\)
\(b,\left\{{}\begin{matrix}a//b\\a\perp c\end{matrix}\right.\Rightarrow b\perp c\)
\(c,\widehat{M_4}+\widehat{M_1}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{M_4}=180^0-75^0=105^0\\ \widehat{N_3}+\widehat{N_4}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{N_3}=180^0-105^0=75^0\)
a) Ta có: \(\widehat{N_1}+\widehat{N_4}=180^0\)(kề bù)
\(\Rightarrow\widehat{N_1}=180^0-\widehat{N_4}=180^0-105^0=75^0\)
\(\Rightarrow\widehat{N_1}=\widehat{M_1}=75^0\)
Mà 2 góc này là 2 góc đồng vị
=> a//b
b) Ta có:
a//b(cmt)
a⊥c(gt)
=> b⊥c(từ vuông góc đến song song)
c) Ta có: \(\widehat{N_3}=\widehat{N_1}=75^0\)(đối đỉnh)
Ta có: \(\widehat{M_4}+\widehat{M_1}=180^0\)(kề bù)
\(\Rightarrow\widehat{M_4}=180^0-\widehat{M_1}=180^0-75^0=105^0\)
a, chứng tỏ ab(a+ b) chia hết cho 2
b, chứng tỏ ab+ ba chia hết cho 11
c , chứng tỏ aaa chia hết cho 37
d , chứng tot aaabbb chia hết cho 37
e, ab- ba chia hết cho 9 với a> b
Cho tam giác ABC vuông tại A có ∠B = 2∠C, đường cao AD.
a) Chứng tỏ ΔADB và ΔCAB đồng dạng
b) Kẻ tia phân giác của góc ABC cắt AD tại F và AC tại E
Chứng tỏ AB2 = AE.AC
c) Chứng tỏ D F F A = A E E C
d) Biết AB = 2BD. Chứng tỏ diện tích tam giác ABC bằng ba lần diện tích tam giác BFC.

a) ΔADB và ΔABC vuông có ∠B chung ∠ ΔADB ∼ ΔCAB (g.g)
b) Vì ∠B = 2∠C (gt) ∠ ∠B1 = ∠B2 = ∠C
Do đó hai tam giác vuông ABE và ACB đồng dạng (g.g)
![]()
c) Ta có ΔADB ∼ ΔCAB (cmt)
![]()
Theo tính chất đường phân giác ta có :

d) Ta có AB = 2BD (gt)
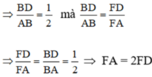
![]()

1.Cho A=4+42+43+....+423+424
a)Chứng tỏ A chia hết cho 20
b)Chứng tỏ A chia hết cho 21
c)Chứng tỏ A chia hết cho 420
a, 3S= 3+ 3^2 +3^3+....+3^2014+3^2015
3S-S=(3+3^2+......+3^2015)-(S=3^0 +3^1 +3^2 + . . . +3^2014)
2S=3^2015-3^0
b,Đề bị sai hay sao????.Thui để sau sẽ có người giúp cậu.Bye Bye!!!!!!!
Tui trả lời câu b nè:
S=(3+3^2+3^4)+...+(3^2012+3^2013+3^2014)
Vì máy tính ko viết được dấu nhân nên tui nói bằng lời còn bạn tự kiểm tra nha
Các tổng trên chia hết cho 7 nên S chia hết cho 7
Đảm bảo là đúng!!! :)
CLGT Minh!
2014 ko chia hết cho 3, ghép thế kiểu ****
theo mình thì đề sai rồi. Số mũ cuối chia hết cho 3 mới giải được
tống đến 2013 chia hết cho 7; 3^2014 ko chia hết được
còn câu a thì nhân tổng S với 3^2 để khử rồi chia cho 8